Simulación numérica de la aplicación de corrientes de inducción al desmontaje eficiente de vías en placa ferroviarias
Numerical simulation of the application of induction currents to the efficient dismantling of slab tracks
Ane Onaindia Rodríguez-Maribona (1), Olatz Oyarzabal de Celis (1), Aimar Orbe Mateo (1), Roque Borinaga Treviño (1), Javier Canales Abaitua (1), Ernesto García Vadillo (1)
Resumen
En la actualidad, gran parte de los sistemas ferroviarios contienen una superestructura basada en la vía en placa. Este tipo de vía se ha convertido en la solución elegida para muchos proyectos de líneas de alta velocidad y túneles gracias a sus múltiples ventajas, entre las que se encuentran el aumento de la fiabilidad, la reducida necesidad de mantenimiento y la facilidad de limpieza y explotación. Sin embargo, el sistema de vía en placa supone un problema cuando es imprescindible su sustitución o reparación debido a causas como un descarrilamiento o el propio final de la vida útil de sus componentes. Por esta razón, a la hora de diseñar nuevas vías en placa, es conveniente estudiar un sistema eficiente de reparación de la vía para suspender los servicios ferroviarios ofertados durante el menor plazo de tiempo posible, limitando afecciones a los usuarios y reduciendo costes para las Administraciones ferroviarias. Este estudio analiza alternativas al proceso de desmontado de los bloques que componen la vía en placa, basando las soluciones en el calentamiento por inducción electromagnética. Mediante el calentamiento por inducción de los bloques que constituyen la vía, se pretende conseguir el agrietamiento superficial de las zonas laterales inferiores del bloque, garantizando así su separación del resto de la vía en placa y asegurando una fácil extracción para, posteriormente, proceder a la colocación del nuevo componente.
Palabras clave: Inducción electromagnética, vía en placa, hormigón armado, desmontaje
Abstract
Today, a number of railway systems have a superstructure based on slab track. This type of track has become the solution chosen for many high-speed line and tunnel projects due to its many advantages, including increased reliability, reduced need for maintenance and ease of cleaning and operation. However, the slab slab track systems have an inherent problem when they need to be repaired due to causes such as a derailment or the end of the use lifespan of its components. For this reason, when designing new slab tracks, it is convenient to study an efficient track repair system to recover the normal rail services as soon as possible, limiting effects on users and reducing costs for railway Administrations. This study analyzes alternatives to the process of dismantling the slab track blocks that support the rails, basing the solutions on heating by electromagnetic induction. Through induction heating of the blocks that are inserted in the slab, the aim is to achieve surface cracking of the lower lateral areas of the block, thus guaranteeing its separation from the rest of the slab track and ensuring easy extraction to subsequently proceed with the placement of the new component.
Keywords: Electromagnetic induction, slab track, reinforced concrete, dismantling
Recibido / received: 17/06/2021. Aceptado / accepted: 20/10/2021.
1 Departamento de Ingeniería Mecánica, Universidad del País Vasco/Euskal Herriko Unibertsitatea.
Autor para correspondencia: Olatz Oyarzabal de Celis; olatz.oyarzabal@ehu.eus
Introducción
Hasta ahora, en el ámbito ferroviario, no era habitual contemplar la reutilización de los recursos a la hora de organizar su construcción. Sin embargo, en las últimas décadas se ha apreciado que, mediante la reutilización o sustitución parcial de diversos componentes, se pueden obtener beneficios económicos significativos en la vida útil del producto final. Por ello, ha aumentado el interés en desarrollar métodos eficientes que permitan llevar a cabo estas operaciones de demolición y sustitución de manera selectiva. Generalmente, la retirada del material de la vía en placa ferroviaria se realiza a través de máquinas Rotaflex y martillos neumáticos, basados en procesos de picado, que generan consecuencias indeseadas como ruido, vibraciones, polvo, etc. Por tanto, en estas soluciones a desarrollar se busca, entre otros, evitar circunstancias indeseadas en el entorno y en los usuarios, considerando suspender el servicio ferroviario durante el menor tiempo posible. Una de las posibles estrategias elegidas para este desempeño es facilitar la retirada del material tras haber provocado un agrietamiento en las superficies adecuadas.
pieza conductora [4]
Entre las posibles soluciones para este tipo de operaciones, se ha decidido profundizar en la demolición selectiva mediante ondas electromagnéticas. El fenómeno de inducción electromagnética es una línea de investigación en crecimiento en el ámbito de la construcción gracias a sus múltiples prestaciones. Mediante este fenómeno se busca conseguir un agrietamiento rápido y eficiente de la superficie de contacto entre el componente a extraer y el resto de la losa. En el presente artículo se analiza la aplicación de ondas electromagnéticas para producir la separación del bloque de hormigón embebido en la losa de hormigón de que se componen ciertos tipos de vía en placa.
Se trata de un análisis inicial de las posibles estrategias para el desmontado eficiente de los bloques basado en el calentamiento por inducción electromagnética, gracias a una fuente inductora que, en este caso, es una bobina de cobre. Mediante este tipo de calentamiento se elevan las temperaturas de las barras de acero distribuidas en el interior del bloque de hormigón, concretamente de aquellas que se encuentran más cercanas al inductor. Con ello, también se calienta el hormigón y el agua que se encuentra en sus poros húmedos. El agua, al alcanzar altas temperaturas se evapora y ejerce una presión sobre las paredes del poro del bloque de hormigón que genera tensiones en él [1, 2]. En el estudio del fallo, de manera simplificada, se comparan las tensiones generadas en el hormigón con las resistencias medias a tracción del material y, en caso de superarlas, se supone el fallo del componente. Se trata de una manera muy elemental de estudiar la fractura, ya que no se considera la generación y propagación de fisuras, por lo que no se apreciará en detalle el agrietamiento a través del recubrimiento hasta llegar a la superficie de contacto del bloque, ni la posterior operación de extracción.
En este documento, primero, se presentan de manera resumida los fenómenos físicos y mecánicos necesarios para la correcta comprensión del calentamiento por inducción y el posterior agrietamiento del bloque de hormigón. A continuación, se explican las pruebas simuladas diferenciando principalmente dos tipos: en cuanto al primer conjunto de pruebas, se busca desarrollar un modelo similar al desarrollado experimentalmente en laboratorio, con la finalidad de validar correctamente los fenómenos magnéticos y de transferencia de calor en el programa de simulación. Tras ajustar los parámetros necesarios para establecer el calentamiento por inducción mediante elementos finitos en COMSOL, se aplican estos fenómenos físicos al nuevo modelo a desarrollar, el bloque perteneciente a la vía en placa ferroviaria. Se estudia el aumento de temperaturas de dicho bloque en los puntos de interés y, finalmente, se analiza el fallo debido a las tensiones generadas (se estudian mediante ANSYS) por ese calentamiento. Si ocurre el fallo en diferentes puntos superficiales del bloque, en líneas futuras de la investigación se analizará el agrietamiento y fractura final, para conseguir, finalmente, el desmontado eficiente del bloque de la vía en placa ferroviaria.
Calentamiento por inducción
El calentamiento por inducción es un método ampliamente utilizado en la industria cuando se busca aumentar la temperatura de un material ferromagnético e, incluso, paramagnético. Este método es una aplicación directa de tres fenómenos fundamentales de la física: dos de las leyes de inducción electromagnética (ley de Faraday y ley de Ampere) y el efecto Joule [3].
De manera esquemática, se va a definir el calentamiento por inducción como un proceso en el que tienen lugar las diferentes fases que se explican a continuación, junto con las ecuaciones correspondientes de forma diferencial:
1. Si por un elemento conductor (elemento 1, primario, bobina en este caso) circula una corriente eléctrica, esta induce un campo magnético en la región (ley de Ampere). Si se trata de una corriente alterna la que circula por el conductor, el campo magnético obtenido es también alterno, es decir, variable en el tiempo. Esta ley se define teóricamente mediante la ecuación diferencial (1), que indica que la circulación de corriente eléctrica por un conductor (por ejemplo, un alambre de cobre) provoca la aparición de un campo magnético “B” rotacional alrededor del alambre, y que el rotor del campo magnético apunta en el mismo sentido que la densidad de corriente “J”. En dicha fórmula se incluye el valor de la constante magnética “?0”, también denominada permeabilidad magnética en el vacío, cuyo valor es 4?·10-7 H/m.
2. Si en la región de un campo magnético variable se encuentra expuesto un objeto (elemento 2, secundario, barras de acero en este caso) ferromagnético y conductor, se induce en él una fuerza electromotriz (f.e.m.) que implica que por este elemento circule una corriente eléctrica (ley de Faraday). Dicho de otra manera, el movimiento relativo entre el material y el campo magnético variable causa que los portadores de carga del material conductor se vean sometidos a una fuerza (f.e.m.) y el movimiento de estas cargas genera una corriente eléctrica inducida dentro del conductor. La corriente inducida en el elemento 2 se denomina “corriente de Foucault”, en inglés Eddy currents. Estas corrientes circulares crean electroimanes con campos magnéticos que se oponen al efecto del campo magnético aplicado (ley de Lenz). Teóricamente, la ley se define mediante la ecuación (2), que indica que el rotacional de un campo eléctrico “E” es proporcional a la variación del campo magnético “B” en el tiempo, incluyendo el signo negativo argumentado mediante la ley de Lenz.
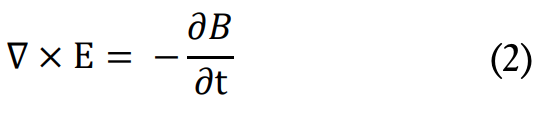3. Por último, la circulación de estas corrientes de Foucault a través del material (barras de acero en este caso) genera pérdidas de energía, lo que deriva en un calentamiento de la pieza en cuestión (efecto Jou- le). El efecto Joule es un fenómeno irreversible por el cual, si por un conductor circula una corriente eléctrica “I”, parte de la energía cinética de los electrones se transforma en calor “Q”. Esto sucede a causa del movimiento desordenado de los electrones que origina continuas colisiones con los núcleos atómicos del material, lo que concluye en una pérdida de energía cinética y un aumento de temperatura del El calor generado/energía térmica disipada por la circulación de la corriente “Q [ J]” se define en la ecuación (3) a partir de la potencia disipada por el conductor “P [W]” y del tiempo durante el que circula la corriente por el conductor “t [s]”. En la fórmula también aparecen los parámetros “R [W]”, que es la resistencia que opone el conductor al paso de la corriente, e “I [A]”, que es la corriente eléctrica que circula por el material.
(3) En la figura 1 se visualiza lo explicado previamente. Mediante la circulación de corriente alterna (CA) a través de una bobina (elemento primario, conductor), se genera un campo magnético alterno. La pieza de acero a calentar (elemento secun- dario, conductor y ferromagnético), atrae las líneas de campo magnético a su interior y comienza la circulación de corriente eléctrica de la corriente “Q [J]” se define en la ecuación (3) a partir de la potencia disipada por el conductor “P [W]” y del tiempo durante el que circula la corriente por el conductor “t [s]”. En la fórmula también aparecen los parámetros “R [?]”, que es la resistencia que opone el conductor al paso de la corriente, e “I [A]”, que es la corriente eléctrica que circula por el material
En la figura 1 se visualiza lo explicado previamente. Mediante la circulación de corriente alterna (CA) a través de una bobina (elemento primario, conductor), se genera un campo magnético alterno. La pieza de acero a calentar (elemento secundario, conductor y ferromagnético), atrae las líneas de campo magnético a su interior y comienza la circulación de corriente eléctrica en el cuerpo [4]. Las corrientes inducidas en el elemento secundario, fluirán en función de un parámetro denominado efecto pelicular/profundidad de piel, en inglés skin effect, que determina que a mayor frecuencia del campo magnético alterno, la circulación de la intensidad por la pieza se realizará de manera más superficial [5]. En el presente caso, interesa emplear una elevada frecuencia porque no se busca el calentamiento interno del elemento ferromagnético, sino el calentamiento superficial de este para que luego se transfiera por conducción al material contiguo.
La gran ventaja de este proceso es conseguir el calentamiento gracias a la creación de un campo magnético, sin necesidad de que la fuente del calentamiento, en este caso una bobina, se encuentre en contacto directo con el destinatario de este calentamiento, que en el presente estudio son las ba- rras de acero. Una ventaja adicional de este método se basa en la capacidad de calentamiento selectivo, pudiendo ele- gir las zonas en las que se desea calen- tar el material. Además, se trata de un proceso limpio, eficiente y controlado que se puede repetir las veces que se desee.
Agrietamiento del material
En este artículo se emplea la teoría de fallo clásica analizando las tensiones que se obtienen en los poros del hormigón debido a la presión ejercida por el vapor de agua en ellos. Una de las características más significativas del hormigón es que tiene una alta resistencia a compresión y baja a tracción, lo que significa que se trata de un material no equirresistente. Se ha decidido emplear la teoría de fallo de Rankine, porque es el criterio de fallo más sencillo, y es válido por ser el más restrictivo. Este método también se denomina “criterio de la máxima tensión normal” e indica que si el máximo de las tensiones principales generadas en el componente (?1 , ?2 , ?3 ) supera o iguala la tensión de rotura del material (?R) (de tracción o compresión), se dará el fallo del material. Por tanto, en el desarrollo del procedimiento se deberán obtener las tensiones generadas en las superficies de los poros del bloque de hormigón y compararlas con la resistencia a tracción y a compresión correspondientes.
Para la obtención de la resistencia media a tracción y a compresión, se necesita definir el hormigón utilizado en la investigación. Se han realizado cálculos utilizando el hormigón HA-25, que es el mínimo permitido por la normativa para hormigones estructurales. Además, los fabricantes de infraestructuras ferroviarias suelen emplear hormigones de mayor resistencia, HA50. En consecuencia, se han desarrollado los cálculos con ambos tipos de hormigones, ya que el hormigón HA25 tiene interés puesto que puede abrir líneas de investigación futuras en aplicaciones diferentes de las ferroviarias.
La resistencia media a tracción “ftm” (MPa) se obtiene a partir de la ecuación (4), siendo “fck” (MPa) la resistencia característica a compresión del hormigón a los 28 dÍas.
Por tanto, se busca el fallo del hor- migón debido a la tracción ejercida por la evaporación del agua de los poros, para lo que se comparan las tensiones generadas a tracción con la resistencia a tracción media del hormigón, que en caso de suponer un hormigón HA-50, es 4,1 MPa.
Ajuste con modelo experimental
Antes de estudiar el calentamiento del bloque perteneciente a la vía en placa, se han simulado mediante el programa COMSOL [6-8] varias pruebas con- sistentes en una bobina helicoidal que calienta por inducción una probeta de mortero con una barra de acero en su interior. Se introducen en el programa las propiedades de los materiales y se obtienen las temperaturas de la barra de acero. Dichos resultados se comparan con los resultados de temperaturas obtenidos en ensayos experimentales de los autores de este artículo.
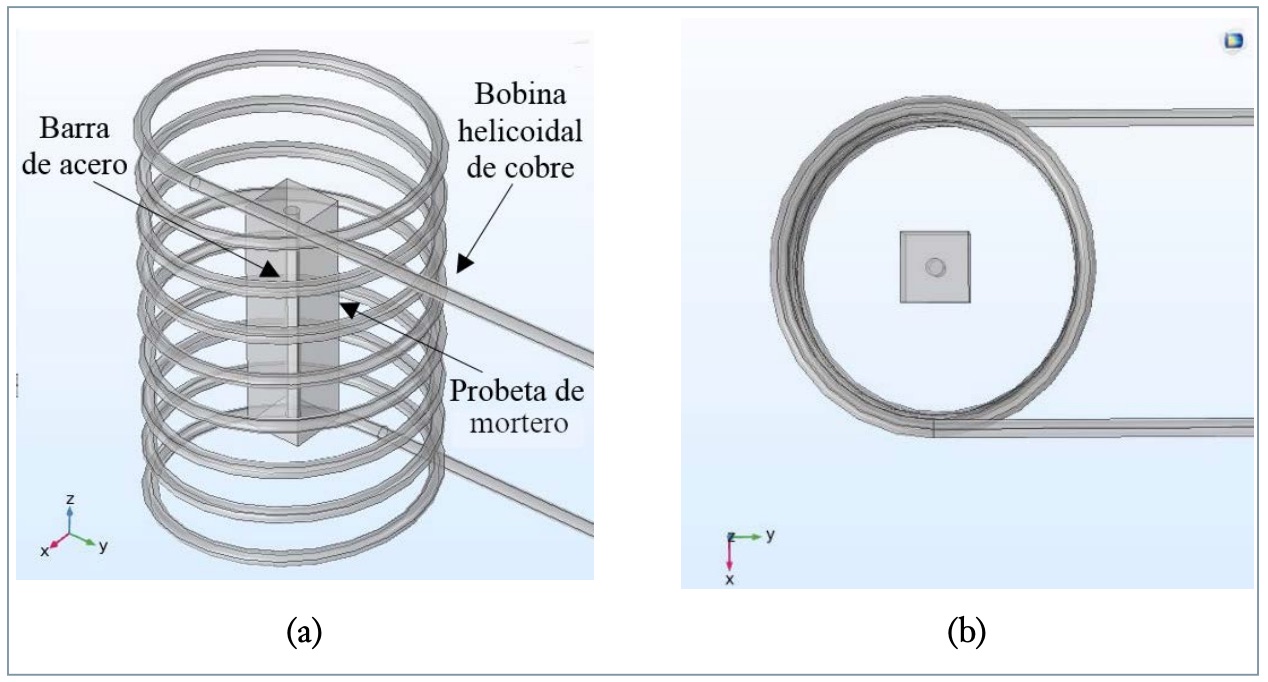
Los parámetros de inducción electromagnética pertenecientes a la fuente de energía (la bobina) son la corriente eléctrica alterna (888 A, valor RMS) y la frecuencia de trabajo (24 kHz). La bobina inductora es de tipo helicoidal con 9 vueltas, un diámetro interior de 170 mm y una altura de 290 mm, como se observa en la figura 2.
Por su parte, la probeta de mortero tiene forma de paralelepípedo y unas dimensiones de 40 mm de lado y una longitud de 160 mm mientras que la barra de acero tiene una longitud de 150 mm y un diámetro variable en función de la probeta correspondiente. Se han ensayado un total de 9 pruebas con diferentes probetas, correspondientes a 3 diámetros diferentes de la barra de acero (8, 10 y 12 mm). Por tanto, las pruebas experimentales realizadas se han denominado de la siguiente manera: 1ø8, 2ø8, 3ø8, 1ø10, 2ø10, 3ø10, 1ø12, 2ø12 y 3ø12.
En la figura 2 se visualiza el sistema ensayado de manera experimental que contiene la bobina de cobre y la probeta de mortero con una barra de acero, aunque esta última no se observa por estar en el interior de la probeta.
En la figura 3 se muestra una de las probetas ensayadas con la identificación en la superficie de la probeta. En las figuras 2 y 3 se aprecia que, unido a las probetas, se encuentran dos cables correspondientes a los termopares, que proporcionan la temperatura a lo largo del calentamiento en el punto medio de la barra de acero y también en el extremo. Estos son los resultados con los que se comparan las temperaturas obtenidas mediante la simulación computacional.
En la figura 4 se visualiza el modelo desarrollado en COMSOL que contiene todos los elementos del modelo ensayado experimentalmente.
Los parámetros geométricos (disposición de la bobina, probeta y barra) y de entrada (intensidad y frecuencia del equipo inductor) son los mismos que en el ensayo experimental. Ha sido laborioso definir correctamente las propiedades de los diferentes materiales para la obtención de las temperaturas en los puntos de interés. Concretamente, se ha comprobado que la conductividad térmica del hormigón y la permeabilidad del acero no son valores constantes, sino que varían con la temperatura. La conductividad térmica del acero es 52,335 W/(m·K) y la del hormigón se encuentra en el rango de valores entre 1,35 y 2 W/(m·K), además de variar con la temperatura según se muestra en Millard et al. [9]. Por otro lado, se ha observado experimentalmente que la permeabilidad relativa del acero va aumentando hasta alcanzar el valor de 37, y disminuye a partir de la temperatura de Curie (768 ºC) hasta el valor unidad.
En la figura 5 se muestra una gráfica correspondiente a la temperatura en el punto medio de la barra de acero. Se visualiza la evolución de la temperatura que alcanza ese punto a lo largo del tiempo, hasta una duración de calentamiento de 250 segundos. En esta figura, se muestran los resultados de tres pruebas simuladas en COMSOL correspondientes a un diámetro de la barra de acero de 10 mm y a diferentes conductividades térmicas del hormigón: PRUEBA 1 (1,35 W/[m·K]), PRUEBA 2 (2 W/ [m·K]) y PRUEBA 3 con un valor de 3 W/(m·K), para estudiar el comportamiento con diferentes conductividades térmicas, además de las pruebas experimentales denominadas 1ø8, 2ø8, 3ø8, 1ø10, 2ø10, 3ø10, 1ø12, 2ø12 y 3ø12.
En la gráfica se aprecia que los resultados experimentales son muy diferentes entre sí, lo que se puede deber a que los termopares no se han soldado a las barras y, por tanto, las medidas pueden no corresponder al punto deseado con exactitud.
Aplicación de corrientes de inducción al desmontado eficiente de vías en placa ferroviarias
La configuración de la vía en placa de estudio se muestra en la figura 6 y consiste en dos bloques prefabricados, inferior y superior, que contienen en su nexo de unión un elastómero (elemento de color rojo en la figura 6), que se vierte en estado líquido y fragua posteriormente. Sobre este conjunto de bloques se colocan los carriles con las correspondientes sujeciones y elastómeros adicionales.
En el proceso de construcción de este tipo de vía se coloca el conjunto completo (carril y sujeciones, bloque superior, elastómero entre bloques y bloque inferior) prefabricado a lo largo de la vía y, posteriormente, se vierte in situ hormigón hasta cubrir por completo el bloque inferior. De este modo, se obtiene una losa de hormigón continua horizontal. Esta disposición de los elementos se aprecia en la figura 7, en la que se visualiza la forma de cola de milano que tiene el bloque superior, lo que dificulta la separación de los dos bloques. Durante el funcionamiento habitual de la vía ferroviaria es deseable que la adhesión bloque superior-bloque inferior mediante el elastómero sea efectiva, pero no es así cuando el objetivo es separar los dos bloques, como es el caso.
En esta investigación se ha estudiado un método para que, en caso de que se requiera reparar o sustituir el bloque superior, no sea necesario demoler toda la vía por completo, sino que se pueda desmontar el bloque superior sin que los elementos inferiores (losa y bloque inferior) se dañen y, por tanto, se puedan seguir utilizando, consiguiendo así un desmontado eficiente de la vía en placa. En consecuencia, se busca separar la zona de nexo entre el bloque superior y el inferior mediante el agrietamiento de la zona superficial de contacto del bloque superior. Lógicamente, antes de comenzar con el proceso de desmontaje de la vía en placa, se deben retirar los carriles y correspondientes sujeciones.
Las altas tensiones en las aristas de los poros de la zona superficial del bloque superior se consiguen mediante la incorporación de materiales ferromagnéticos y conductores, en este caso barras de acero, en la zona superficial que se desea agrietar. El proceso consiste en aplicar, a través de una bobina de cobre, un campo magnético con el que se inducen corrientes eléctricas en las barras de acero insertadas en el bloque. Debido a la circulación de corriente por las barras, estas se calientan elevando las temperaturas del bloque de hormigón completo.
Al calentarse todo el bloque de hormigón, también lo hace el agua que se encuentra en los poros del hormigón. El agua, al superar los 100 ºC, se evapora y ejerce presión sobre las paredes de los poros del hormigón. Si la presión ejercida es suficientemente alta, las tensiones generadas en el hormigón serán superiores a su resistencia a tracción y el hormigón falla, por lo que surge un agrietamiento en la zona donde se han colocado las barras. En el caso de estudio, interesa agrietar y fracturar la zona de contacto entre bloque superior e inferior de la figura 7, por lo que las barras de acero se colocan lo más cerca posible de la superficie del bloque superior de hormigón, dejando el recubrimiento necesario. Una vez agrietado el bloque en la zona deseada, con las herramientas correspondientes se extraería el bloque superior, se retira el elastómero residual y se procede a la colocación de un bloque superior y elastómero nuevos.
Modelización por elementos finitos del calentamiento por inducción del bloque de la vía en placa
En la figura 8 se muestra el modelo desarrollado en COMSOL consistente en un bloque de hormigón, con las barras de acero y añadiendo unos cubos que simulan los poros con agua del hormigón poroso. Cabe destacar que los poros del hormigón tienen un tamaño muy pequeño en la realidad, aunque en las simulaciones se han utilizado dimensiones en forma de cubo de 6 mm de lado para simular el poro, porque un tamaño menor supone un gasto computacional demasiado elevado.
En la figura 9 se muestran las líneas del “eje x” (y = 0, en el centro del bloque) de las que se va a mostrar la temperatura. Las líneas (roja, morada y azul) con las cotas impares pasan por el centro de las barras de acero, mientras que las líneas (verde y amarilla) con las cotas pares corresponden a los poros de agua (todos los centros situados en x = 0,13 m).
En la figura 10 se muestra un gráfico con las temperaturas alcanzadas tras 5 minutos de calentamiento por inducción a lo largo de los ejes x definidos en la figura 9. La temperatura en la barra central (línea roja, z = 0,03 m) es la que mayores temperaturas alcanza (400 ºC), seguida de las barras de los lados (líneas morada y azul, z = 0,05 y 0,01 m), que superan los 350 ºC. Los poros húmedos (línea verde y amarilla, z = 0,04 y 0,02 m), por su parte, también presentan un pico de crecimiento de temperatura en x = 0,13 m, debido al calor por conducción transferido desde las barras, superando en los puntos destacados los 250 ºC.
Las temperaturas de los puntos destacados en las líneas que pasan por las barras se muestran en la tabla 1.
(líquido-vapor).
Por otro lado, en la figura 11 se muestran 5 puntos de uno de los poros estudiados. Estos puntos se han destacado para mostrar la temperatura que han alcanzado a los 5 minutos de calentamiento, y esta temperatura es la que se utiliza para estudiar si el material falla.
A continuación, en la tabla 2 se muestran las temperaturas alcanzadas por los puntos destacados de los poros. Las temperaturas en los diferentes puntos de los poros con agua superan todas los 250 ºC, pero no los 300 ºC. Para estudiar el agrietamiento del bloque en ANSYS, en el siguiente epígrafe, se supone que todos los puntos del poro alcanzan la misma temperatura y con ese dato se obtiene la presión de expansión ejercida en las paredes del poro debido al calentamiento y a la evaporación del agua. Con la presión obtenida, se estudia si el material falla. Por tanto, se ha decidido que la temperatura utilizada en el siguiente epígrafe sea 250 ºC, que es el valor superado por todos los puntos de interés.
Estudio del agrietamiento
Tras la obtención de las temperaturas que alcanzan los poros de agua, se procede a calcular, mediante la expansión del vapor de agua, que genera presiones en el hormigón, las tensiones de la zona superficial del bloque. En la tabla 3 se muestran la relación temperatura-presión del agua saturada en la que se obtiene la presión ejercida por el vapor de agua al alcanzar diferentes temperaturas. En la tabla 3 se observa que las gotas de agua tras el calentamiento por inducción durante 5 minutos superaban todas los 250 ºC, por lo que se supone una presión ejercida hacia el hormigón por parte del agua evaporada de 3.973 MPa.
El estudio de las tensiones del material se ha analizado mediante el programa ANSYS [11] modelizando un elemento de hormigón con un hueco en medio (mismas dimensiones del poro en COMSOL), como se aprecia en la figura 12, sin simular el bloque entero de hormigón como en la figura 8. Se considera esta simplificación porque las presiones generadas debido a la expansión del vapor de agua afectan, sobre todo, al material alrededor del hueco.
Tras ejecutar la simulación, se obtienen las tensiones generadas en las tres direcciones (x, y, z), y los valores son similares entre ellos dado que las presiones ejercidas se han introducido de manera idéntica en todas las paredes del hueco. Las tensiones en el eje x se muestran en la figura 13, en la que se observan las tensiones de tracción generadas etiquetadas, con valores de 4,8, 5,8, 6,3, 6,1 y 5,9 MPa, todos ellos superando la resistencia media a tracción del hormigón HA-50 utilizado en infraestructura ferroviaria, es decir, superando 4,1 MPa (obtenida en el epígrafe Agrietamiento del material).
En resumen, tras este análisis en ANSYS, se destaca que el hormigón, teóricamente, fallaría si se alcanza en los poros de hormigón una temperatura del agua de 250 ºC o superior.
Conclusiones
El objetivo de este artículo es presentar la estrategia desarrollada para un futuro diseño de vía en placa ferroviaria con criterios de desmontado eficiente de apoyos mediante la aplicación del calentamiento por inducción. El empleo de esta técnica electromagnética presenta múltiples ventajas como la reducción del ruido, vibraciones, polvo, etc. respecto a los actuales métodos de picado utilizados para el desmontado de los bloques pertenecientes a la vía en placa.
Primero se ha obtenido satisfactoriamente un modelo en COMSOL a partir de los modelos experimentales sobre las probetas ensayadas en laboratorio. De esta manera, se han obtenido los parámetros necesarios para simular correctamente el calentamiento por inducción.
A continuación, se ha simulado el modelo de bloque perteneciente a la vía en placa y se puede afirmar que, mediante unas condiciones de funcionamiento de trabajo de la bobina de inducción dadas (intensidad y frecuencia dentro del rango habitual de equipos comerciales disponibles en el mercado), se puede obtener un calentamiento elevado de las barras de acero pertenecientes al bloque. También se obtiene un calentamiento del agua en los poros del hormigón por encima de los 250 ºC.
Además, se ha comprobado utilizando elementos finitos que, mediante el calentamiento por inducción, se obtienen altas tensiones en las aristas de los poros del hormigón, por lo que ocurre el fallo del material, lo que su pone la fisuración de la superficie del bloque de la vía en placa que se desea agrietar.
En conclusión, esta solución de demolición eficiente permite el calentamiento deseado y posterior agrietamiento en un tiempo suficientemente reducido (5 minutos), por lo que se considera una aplicación válida. Adicionalmente, se recuerda que mediante este método no se necesita contacto directo entre la fuente (bobina inductora) y el objeto a calentar (las barras o fibras de acero), lo cual es una ventaja notable que considerar.
Agradecimientos
Este trabajo se ha financiado en parte por European Horizon 2020 Joint Technology Initiative Shift2Rail a través del contrato No 101012456 (IN2TRACK3). Los autores también desean agradecer al Ministerio de Investigación español MICINN/Ministerio de Economía y Competitividad MINECO su financiación a través del contrato PID2019-109483RB-I00, incluida la financiación del Fondo Europeo de Desarrollo Regional FEDER-ERDF, y al Gobierno Vasco por su financiación con IT1764-22 e IT1619-22.
Referencias
[1] Ahn J., Noguchi T., Kitagaki R. “Disassembly properties of cementitious finish joints using an induction heating method”. Mater;8: 2433-53 (2015).
[2] Lim M., Lee JS. “Economic feasibility of the induction heating method for dismantling structures: Analysis of reinforcement recovery costs based on required demolition equipment”. Int J Appl Eng Res, 12:13077-83 (2017).
[3] Acevedo A., Barrero J., Augusto J. “Calentamiento por inducción electromagnética: Diseño y Construcción de un prototipo”. UIS Ingenierías, Volumen 6, No.1, 69-76 (2007).
[4] Davies E. J. “Conduction and Induction Heating”. IEE Power Engineering Series II, 75-85 (1990).
[5] Lupi S., Forzan M., Aliferov A. “Induction and Direct Resistance Heating, Theory and Numerical modeling., 8-12 (2015).
[6] Djellabi K., Latreche M. E. H. “Induction Heating Process Design Using Comsol Multiphysics Software Version 4.2ª”. World Academy of Science, Engineering and Technology International Journal of Electrical and Computer Engineering, Vol 8, No:1, (2014).
[7] AC/DC Module: User’s Guide, COMSOL MULTIPHYSICS, (2018).
[8] Heat Transfer Module: User’s Guide, COMSOL MULTIPHYSICS, (2018).
[9] Millard A., Pimienta P. (Eds.). “Modelling of Concrete Behaviour at High Temperature” State-of-the-Art Report of the RILEM Technical Committee 227-HPB. Springer, Cham. (2019).
[10] Borinaga R. et al. “Deliverable D.3.2 Track and track component design and performance, demonstrators and simulations”, Proyecto In2Track2, Shift2Rail, UPV/EHU (2020).
[11] Zecher J. “ANSYS Workbench Software, Tutorial with Multimedia CD”. SDC Publications (2009).
