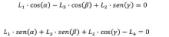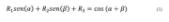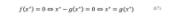Metodología para la optimización del mecanismo de suspensión trasera de una motocicleta de competición
Methodology for optimizing the rear suspension mechanism of a racing motorcycle
Resumen
El comportamiento del sistema de suspensión trasera de una motocicleta depende de la forma en que el mecanismo transmite las cargas del contacto neumático-carretera al amortiguador. Actualmente la obtención de la mejor configuración de la suspensión trasera de una motocicleta se realiza por métodos experimentales. este artículo propone un método de optimización de las dimensiones del conjunto bieleta-balancín utilizando la síntesis de Freudenstein. esto permite determinar la configuración óptima para que el amortiguador trabaje a lo largo de todo su recorrido, teniendo en cuenta las limitaciones de espacio, de la forma más eficiente. Con esta metodología es posible mejorar el contacto neumático-carretera y, con este, la dinámica de la motocicleta.
Recibido: 20 de mayo de 2016
Aceptado: 3 de junio de 2016
Palabras clave
Basculante, balancín, bieleta, amortiguador, suspensión trasera de motocicleta, síntesis de Freudenstein, optimización de mecanismos, motocicleta de competición
Abstract
Motorcycle rear suspension behaviour depends on the way the mechanism transmits loads from tyre-road contact to the shock absorber. Nowadays approaching the best mechanism configuration for a motorcycle rear suspension has been resolved as an experimental issue. This article proposes a method for optimizing rocker arm and tie rod dimensions by using Freudenstein synthesis. This allows to determine the optimal configuration through all the shock absorber travel distance and, according to the space limitations, in a more efficient way. With this method it is possible to improve tyreroad contact and motorcycle dynamics.
Received: May 20, 2016
Accepted: June 3, 2016
Keywords
Swingarm, rocker arm, tie rod, shock absorber, motorcycle rear suspension, freudenstein synthesis, mechanism optimization, competition motorcycle
Introducción
El sistema de suspensión trasera de una motocicleta suele contar con la problemática de que el amortiguador debe asumir los movimientos relativamente amplios que experimenta el basculante en un espacio reducido. Esto implica la necesidad de un mecanismo de bieletas que reduzca este recorrido y otorgue cierta progresividad a la aplicación de la carga sobre el amortiguador.
Optimizando las dimensiones de este mecanismo se logra que el amortiguador actúe de manera progresiva a lo largo de todo su recorrido, absorbiendo tanto pequeñas oscilaciones como grandes impactos y obteniendo una buena respuesta en adherencia de la motocicleta.
Actualmente, los estudios realizados sobre la optimización del mecanismo de bieleta-balancín del sistema de suspensión trasera de motocicletas se basan en el empleo de métodos numéricos1, pero no utilizan una metodología sistemática ni cálculos analíticos. Por otra parte, a nivel de competición, los criterios utilizados para la obtención de la configuración del mecanismo de bieletas de la suspensión trasera suelen ser confidenciales y obtenidos al tanteo.
En este trabajo se presenta una metodología que, utilizando la síntesis de Freudenstein, permite efectuar el cálculo de las dimensiones óptimas del conjunto de bieletas del sistema de suspensión trasera de una motocicleta de competición. Aplicando esta metodología, se logra que el amortiguador actúe a lo largo de todo el recorrido de oscilación del basculante, permitiendo optimizar el comportamiento de la suspensión.
Definición del problema
El sistema de suspensión trasera se basa en el utilizado por la Suzuki Hayabusa de 2008. Se compone de un basculante de doble brazo de aluminio, una bieleta anclada al basculante, un balancín anclado al chasis y un amortiguador que ancla a este. El conjunto bieleta-balancín se encuentra en la parte inferior del basculante. El amortiguador se dispone en posición vertical.
En la figura 1 se representa el funcionamiento del mecanismo de suspensión trasera. Los anclajes al chasis se modelizan como apoyos simples que permite la rotación.
Para regular el comportamiento del sistema de suspensión trasera solo se puede actuar sobre las dimensiones de la bieleta y del balancín. El basculante es un elemento de fabricación compleja: variar sus parámetros supondría un coste económico muy elevado. De igual forma, el amortiguador, al ser un elemento comercial, tiene dimensiones fijas. De ello se concluye que solo se puede actuar sobre las dimensiones de la bieleta y del balancín, elementos de tamaño reducido, gran sencillez y versatilidad de fabricación y reducido coste. En la figura 2 se resaltan la bieleta y el balancín: piezas por determinar.
Objetivos
Con este trabajo se pretende desarrollar una herramienta que combine cálculos algebraicos y representación gráfica que, aplicando la síntesis de Freudenstein, permita ajustar el sistema de suspensión trasera de una motocicleta de competición.
Utilizando esta herramienta, se puede plantear un procedimiento de cálculo para determinar la configuración óptima del mecanismo de bieleta-balancín de la suspensión que permita que el amortiguador actúe en todo su recorrido, mejorando el contacto neumático-carretera y, con él, el comportamiento en marcha de la motocicleta.
Cálculo del comportamiento geométrico del mecanismo
Simplificación bidimensional del problema
El comportamiento de un basculante de motocicleta, en su uso en servicio, es tridimensional. Esto se debe a las deformaciones que este experimenta por las características elásticas de los materiales.
Puesto que los movimientos que experimentará el sistema de suspensión durante la circulación de la motocicleta serán mucho mayores que las deformaciones elásticas de cada uno de sus componentes, se asume que los únicos desplazamientos relevantes se encuentran en el plano medio de la motocicleta. Aplicando este criterio se puede simplificar el comportamiento tridimensional a un comportamiento bidimensional.
Reducción al mecanismo básico: cuadrilátero articulado
El conjunto de componentes del sistema de la suspensión puede modelarse como un conjunto de barras y triángulos articulados en sus extremos: el basculante y el balancín actuarían como dos triángulos y la bieleta y el amortiguador como dos barras. En la figura 3 se representa esta simplificación.
Observando el mecanismo simplificado se comprueba que las únicas barras con relevancia cinemática son las representadas en color naranja (véase la fig. 3). Estas cuatro barras conforman un cuadrilátero articulado que es el mecanismo básico que interviene en el movimiento del sistema de suspensión.
De esta forma, se puede equiparar el funcionamiento del sistema de suspensión al de un cuadrilátero articulado formado por cuatro barras L1, L2, L3 y L4 según la figura 3.
Resolución por síntesis de Freudenstein
La síntesis de Freudenstein determina las dimensiones de un mecanismo que cumpla una función de movimiento determinada.
Para el caso de estudio del comportamiento del sistema de suspensión, la función de movimiento que se pretende conseguir se basa en la relación que existe entre el ángulo del basculante y la longitud del amortiguador.
No obstante, la síntesis de Freudenstein se aplica al cuadrilátero articulado, por lo que sería preciso encontrar una relación entre los movimientos del sistema de suspensión y los del cuadrilátero.
Tanto el basculante como el balancín, en su comportamiento como sólidos rígidos, permiten obtener una relación entre el ángulo del basculante, la longitud del amortiguador y el giro de las barras del cuadrilátero articulado. De esta forma se puede reducir el estudio cinemático del comportamiento del sistema de suspensión trasera de la motocicleta al comportamiento de un mecanismo del tipo cuadrilátero articulado.
1) Aplicación de la síntesis de Freudenstein
Como el mecanismo del sistema de suspensión está compuesto por cuatro barras, el sistema de ecuaciones que plan-tea la síntesis tendrá cuatro incógnitas y, por ende, cuatro ecuaciones. Sin embargo, las barras L1 y L4, según la figura 3, hacen referencia a relaciones geométricas de puntos de anclaje de elementos estructurales como son el basculante y el chasis, los cuales no pueden variar. Por ello, la longitud de estas dos barras son constantes, lo que reduce el problema a un sistema de dos ecuaciones.
Para plantear las ecuaciones de la síntesis de Freudenstein es necesario especificar la relación de posición entre las señales de entrada y las de salida. En este caso, al haberse reducido el sistema a dos ecuaciones solo serán necesarias dos relaciones: las correspondientes a los ángulos máximo y mínimo del basculante y las longitudes máxima y mínima del amortiguador.
La resolución que proponía Freudenstein de un cuadrilátero articulado utilizando su síntesis suponía que la barra que representa la distancia entre los puntos de anclaje del mecanismo se posiciona en horizontal y es de valor unitario. De igual forma, se proponía referenciar los ángulos de cada barra al mismo sistema de referencia. Para este estudio, por las características que muestra el sistema de suspensión de la motocicleta, se ha optado por resolver un cuadrilátero articulado con las condiciones que se muestran en la figura 4: el elemento fijo se encuentra en posición vertical y la barra L4 de longitud conocida y los ángulos obedecen a sistemas de referencia relativos.
A partir del cuadrilátero articulado se plantean las ecuaciones de cierre (véase la fig. 4).
En las ec. (1) y (2) se posicionan los términos dependientes del ángulo a la derecha de ambas igualdades. Se eleva (1) y (2) al cuadrado y se suman entre sí. De la ecuación resultante se agrupan los términos L1, L2, L3 y L4 en tres contantes R1, R2 y R3 en la ec. (3), obteniendo una relación entre las incógnitas α y β
Donde:
Con las fórmulas de las ec (10) y (11) y para obtener un valor optimizado de L2 y L3, se definirán los valores de α1, α2, β1 y β2. Para calcularlos es necesario determinar la relación existente entre los parámetros de entrada y salida del sistema: el ángulo del basculante y la longitud del amortiguador respectivamente.
Equivalencia entre parámetros de entrada
Aunque el mecanismo básico del sistema de suspensión puede equipararse a un cuadrilátero articulado, los parámetros que este regula no son los mismos que se necesitan para restringir el comportamiento de la suspensión.
Para delimitar el sistema de suspensión se utilizan como valores de entrada los ángulos máximo y mínimo del basculante frente a las longitudes máxima y mínima del amortiguador. De esta forma se asegura que el amortiguador trabaja en todo su recorrido.
Sin embargo, los parámetros de entrada del cuadrilátero articulado son los ángulos que rota la barra de entrada frente a la de salida. Por ello es preciso encontrar una relación entre estos parámetros. Estas relaciones se obtienen por trigonometría. En la figura 5 se representa la relación de ángulos y longitudes del sistema de suspensión simplificado.
La primera equivalencia que obtener es la que relaciona el ángulo del basculante con el ángulo de la barra L1 (véase la fig. 5). Esta relación se puede deducir como una suma de ángulos,
La segunda equivalencia vincula la longitud del amortiguador con el ángulo de la barra L3. Esta equivalencia, requiere el valor de L3, ya que esta medida de la bieleta es determinante en el comportamiento cinemático del mecanismo. Por ello, para la resolución del mecanismo completo, será necesario realizar un proceso de iteración, tal como se explicará en el apartado siguiente. Para este cálculo, se utilizan las siguientes relaciones:
De lo que se obtiene:
Método de iteración
Para encontrar la relación existente entre la longitud del amortiguador y el ángulo que gira la barra de salida del cua-drilátero articulado (L3, según la fig. 5) es necesario conocer el valor de L3. Por ello, se utiliza un proceso de resolución numérica basado en el método del punto fijo2.
Este método consiste en reescribir una función f (x) = 0 como x = g(x). Si se supone x* como solución de la función se puede deducir que:
Puesto que el valor de x* se desconoce, se parte de un valor aleatorio de x. Utilizando este valor inicial aleatorio se calcula un nuevo valor de x a partir de la función g de la ec. ( 17 ).
La convergencia del método radica en que los valores xn+1 y de xn sean cada vez más cercanos hasta aproximarse a la propiedad de x* = g(x*), es decir, xn+1(xn). Como criterio de convergencia se utiliza la expresión |xn-xn-1|≤10-12 En el momento en que se cumpla este criterio se toma el valor de xn como solución del problema.
Para este estudio, la función g(x) equivaldría al procedimiento de cálculo basado en la obtención de las dimensiones de la bieleta y balancín, el cual, como valor de x, requiere el valor de L3 (véase la fig. 3). Se toma un valor inicial aleatorio de L3 con el que se realizan los cálculos para determinar la longitud de la bieleta y el balancín. Estos cálculos devuelven los valores de L2 y L3 (véase la fig. 3). Con este valor de L3 se realizan nuevamente los cálculos y se obtiene un nuevo valor de L3 y así sucesivamente hasta que el valor de L3 empleado en el cálculo y el obtenido cumplan el criterio de convergencia.
Modelización numérica y optimización del mecanismo
Dada la complejidad y número de operaciones de los cálculos que determinan el comportamiento geométrico del mecanismo es preciso resolverlo utilizando métodos numéricos.
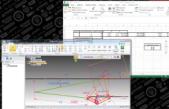
Optimización del mecanismo utilizando excel y solidedge
Para la resolución se utiliza el programa de diseño asistido por computador CAD: SolidEdge. Las ventajas que otorga este programa en comparación con otros de resolución matemática radica en un entorno gráfico muy visual y una gran rapidez a la hora de plantear el problema. Sin embargo, en lo referente a la resolución de ecuaciones, el programa muestra ciertas limitaciones, por lo que se combina con la hoja de cálculo Microsoft Excel para resolver el sistema de ecuaciones y mostrar los resultados numérica y gráficamente en SolidEdge.
En la figura 6 se muestra el procedimiento de cálculo utilizado con los dos programas.
Determinación de las restricciones del problema
La obtención de las restricciones del comportamiento del sistema de suspensión parte de la geometría del diseño de la motocicleta. Para determinar el mínimo ángulo del basculante se tienen en cuenta posibles colisiones con el subchasis o con el colín, mientras que para el ángulo máximo se considera la capacidad máxima de giro que permite la unión del chasis con el basculante en su punto de pivote. Equiparando estos valores con las características del amortiguador que se quiere utilizar, se determinan los dos puntos de funcionamiento de la suspensión. Por medio de las equivalencias correspondientes entre estos puntos y los ángulos de movimiento del cuadrilátero articulado se determina la longitud óptima de las dos bieletas.
No obstante, aún es preciso ajustar el comportamiento que tendrá cada elemento mecánico con respecto a los demás. La síntesis no tiene en cuenta posibles colisiones entre elementos que impidan desarrollar completamente el movimiento oscilante de la suspensión.
El sistema de resolución planteado con Excel y SolidEdge es únicamente una herramienta utilizada dentro de la metodología de obtención de la geometría óptima del sistema de suspensión.
Siguiendo estas ecuaciones combinadas con la representación gráfica que hace de ellas SolidEdge se pueden ajustar los parámetros del conjunto de la suspensión hasta encontrar una geometría que cumpla las restricciones pertinentes, sea fabricable y no incurra en incongruencias físicas.
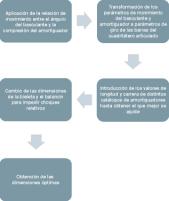
El proceso de obtención de la geometría óptima sigue el esquema mostrado en la figura 7.
Resultados
Utilizando la metodología anteriormente descrita y con la ayuda de la herramienta de cálculo desarrollada en función de la síntesis de Freudenstein se puede comprobar la disposición del mecanismo de la suspensión trasera para distintas configuraciones de bieletas.
En las figuras 8 y 9 se ha planteado un estudio en el que se muestra la longitud de la bieleta y del balancín en función de la longitud máxima del amortiguador y su carrera (como longitud mínima se considera la longitud máxima del amortiguador menos su carrera).
Finalmente, tras un largo proceso de sucesivas iteraciones y comparación de los distintos parámetros de un gran número de amortiguadores y de configuraciones, se concluyó el estudio con una geometría óptima, como la que se muestra la figura 10.
Como se hace patente en la figura 11 el comportamiento del diseño final basado en esta optimización se ajusta perfectamente a las restricciones impuestas para los ángulos máximo y mínimo en comparación con el ángulo en el que el basculante se encontrará soportando el peso de la moto y el piloto en estático.
Conclusiones
En este artículo se propone un modelo de suspensión trasera mejorado para una motocicleta de competición basado en el sistema de suspensión de una motocicleta Suzuki Hayabusa de 2008. Las dimensiones ideales del sistema de suspensión se obtienen mediante la aplicación de una metodología original desarrollada a lo largo de este trabajo, basada en la optimización de las dimensiones del conjunto de bieleta-balancín del sistema de suspensión de la motocicleta para lograr que el amortiguador actúe a lo largo de todo su recorrido.
Esta metodología hace uso de una herramienta de cálculo que determina las dimensiones óptimas del conjunto bieleta-balancín para que en el sistema de suspensión de la motocicleta exista un concordancia entre el ángulo máximo y mínimo del basculante y la longitud máxima y mínima del amortiguador. Se propone utilizar la síntesis de Freudenstein para obtener las longitudes de cada elemento de este mecanismo para que desarrolle un movimiento impuesto. Esta restricción de movimiento se aplica según los ángulos máximo y mínimo del basculante y las longitudes máxima y mínima del amortiguador. Mediante relaciones trigonométricas se equiparan estos criterios a los ángulos de entrada y salida del cuadrilátero articulado.
Se presenta una herramienta, combinación de la hoja de cálculo Microsoft Excel y el programa de CAD SolidEdge, que realiza los cálculos de resolución del mecanismo y muestra gráficamente la geometría resultante.
Finalmente, siguiendo la metodología propuesta, se ajustan los parámetros del mecanismo de suspensión hasta que el comportamiento se adecúe a las limitaciones impuestas por la geometría de la moto y las características del amortiguador.
Aunque la metodología se ha aplicado al sistema de suspensión trasera de una motocicleta de competición, esta puede aplicarse igualmente a cualquier tipo de motocicleta variando las restricciones que se quieran imponer.
Utilizando esta metodología se obtienen dos gráficos que representan las dimensiones del conjunto bieleta-balancín en función de distas longitudes de amortiguador y distintas carreras. Estos gráficos serán de gran ayuda a la hora de determinar la configuración óptima del sistema de suspensión de la motocicleta en función del tipo de amortiguador que se implemente.
Referencias
1. Š. Segla, O. Antonescu, M. Orecný y A. Elbaghar (2015). Optimization of a Motorcycle Rear Suspension Mechanism with Four-bar Linkage. Acta Mechanica Slovaca, 19 (1): 6.
2. R. P. Agarwal, M. Meehan y D. O’Regan (2001). Fixed point theory and applications, Fixed point theory.
3. V. Cossalter (2006). Motorcycle dynamics.
4. P. Thede (2010). Race Tech’s motorcycle suspension bible, Motorbooks.
5. T. Foale (2003). Motocicletas: comportamiento dinámico y diseño de chasis: el arte y la ciencia. Tony Foale Designs.
6. F. Freudenstein (1954). Design of Four-link Mechanisms. Ph. D. Thesis, Columbia, p. 28.





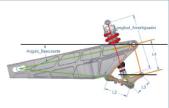
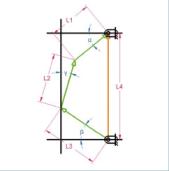
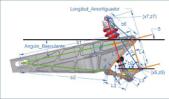 Figura 5. Relación de ángulos y longitudes del sistema de suspensión.
Figura 5. Relación de ángulos y longitudes del sistema de suspensión.