Desarrollo de un método multibloque para la generación automatizada de mallas tridimensionales de engranajes

Víctor Roda-Casanova (1), Francisco Sánchez-Marín (1), Javier Andrés de la Esperanza (1)

Resumen
En este trabajo se presenta un nuevo método para la generación automatizada de mallas tridimensionales de engranajes. Para ello, se siguen los pasos característicos de un método de mallado multibloque para generar una malla de cuadriláteros sobre una sección plana del engranaje, que posteriormente se extruye a lo largo de su ancho de cara para obtener una malla tridimensional de hexaedros. El método de mallado propuesto persigue el objetivo de superar las limitaciones observadas en los métodos tradicionales de mallado de engranajes, lo que permite el refinamiento localizado de la malla y minimiza la distorsión de los elementos. Su funcionamiento se ilustra con ejemplos numéricos que demuestran su capacidad para mallar geometrías de engranaje bajo distintas condiciones de mallado.

Palabras clave: Transmisiones de engranajes, análisis por el método de los elementos finitos, generación de malla

Abstract
A new method for the automated generation of three-dimensional meshes of gears is presented in this work. To do this, the characteristic steps of a multiblock meshing method are followed to generate a quadrilateral mesh on a flat section of the gear, which is, subsequently, extruded along its face width to obtain a three-dimensional mesh of hexahedrons. The proposed meshing method pursues the goal of overcoming the limitations observed in traditional gear meshing methods, allowing localized mesh refinement and minimizing element distortion. Its functioning is illustrated with numerical examples that demonstrate its ability to mesh gear geometries under different meshing conditions.

Keywords: Gear drives, finite element analysis, mesh generation

---

Recibido / received: 16/06/2021. Aceptado / accepted: 28/10/2021.

1 Departamento de Ingeniería Mecánica y Construcción, Universitat Jaume I.

Autor para correspondencia: Víctor Roda-Casanova; e-mail: vroda@uji.es.

---

Introducción
El análisis por el método de los elementos finitos desempeña un papel importante durante las fases de desarrollo de transmisiones de engranajes, pues permite determinar el estado tensional de los engranajes bajo carga [1,2], investigar la formación del contacto entre dientes [3-5] y predecir el campo de temperatura de los engranajes en condiciones de servicio [6,7], entre otras cosas. La realización de un análisis por el método de los elementos finitos requiere del desarrollo de un modelo de elementos finitos de la transmisión, que se consigue mediante tres tareas [8]: (1) generación de la malla de elementos finitos de las geometrías de engranajes, (2) definición de las geometrías de contacto y (3) establecimiento de las condiciones de contorno y de carga de la transmisión.

En el primera de estas tareas se genera la malla de elementos finitos de la transmisión. Esta tarea se puede dividir en dos pasos secuenciales: en primer lugar, se obtiene una definición computacional de las geometrías de los engranajes y, en el segundo paso, estas geometrías de engranaje se discretizan en elementos finitos para obtener la malla de la transmisión.

La manera en la que se realizan estos pasos ha dado lugar a distintos métodos de generación de mallas de elementos finitos de una transmisión de engranajes. Algunos de estos métodos [7,9,10] se basan en la utilización de programas de diseño asistido por ordenador (CAD) para generar las geometrías de los engranajes que, posteriormente, se importan a programas comerciales de análisis por el método de los elementos finitos, donde se discretizan en elementos finitos utilizando los métodos de mallado implementados en el programa. En otros métodos [3,5,11], las geometrías de los engranajes se generan directamente dentro de los programas de análisis por el método de los elementos finitos, implementando algoritmos que permiten obtener una definición matemática de las superficies de los engranajes.

Los métodos descritos anteriormente tienen ciertas desventajas, como el bajo nivel de precisión con el que se definen las geometrías de los engranajes, dependencia de programas de terceros, dificultades a nivel de usuario, etc. Por ese motivo, como explica Hotait [1], resulta mucho más interesante desarrollar programas propios dedicados a la generación de modelos de elementos finitos de transmisiones de engranajes.

Estos programas requieren del desarrollo de métodos de mallado que permitan discretizar las geometrías de los engranajes en elementos finitos. Entre los métodos desarrollados para ese propósito, el más destacable es el propuesto por Argyris [12], puesto que ha sido extensamente utilizado por la comunidad científica [4,6,13-16]. Este método de mallado representa una manera rápida y sencilla de discretizar una geometría de engranaje en elementos finitos, pero tiene algunas limitaciones importantes.

Por una parte, el método propuesto por Argyris tiende a generar elementos distorsionados en algunas partes de la geometría del engranaje que pueden comprometer la precisión de los resultados del análisis [17]. Por otra parte, este método de mallado no permite la realización de refinamiento local de la malla, puesto que genera mallas simétricas en la parte conductora y conducida del diente [18]. Sin embargo, la capacidad de realizar refinamiento localizado de la malla es una característica importante de los métodos de mallado, ya que permite optimizar el número de nodos y de elementos en la malla y reducir el coste computacional asociado al modelo.

En los últimos años ha habido intentos de implementar refinamiento local de la malla en los métodos de mallado de engranajes [19,20], y los más relevantes son los propuestos por González-Pérez [18,21]. En estos trabajos, Gónzalez-Pérez ha mejorado el método propuesto por Argyris habilitando la posibilidad de realizar refinamiento localizado de la malla en la zona en la que se produce el contacto entre dientes. Para ello, se generan mallas independientes en las zonas refinadas, que se conectan a las mallas bastas utilizando restricciones multipunto (MPC). Sin embargo, la utilización de restricciones multipunto para unir mallas no conformes tiende a ser compleja desde un punto de desarrollo del modelo de elementos finitos [22] y puede introducir errores numéricos en las interfaces entre zona basta y zona refinada [23]. Además, los métodos de mallado propuestos por González-Pérez no evitan la generación de elementos distorsionados fuera de las áreas refinadas.

A pesar de los avances hechos en el ámbito del análisis por el método de los elementos finitos de transmisiones de engranajes, los métodos de mallado existentes todavía tienen algunas carencias que es necesario resolver. Por tanto, el objetivo de este trabajo es desarrollar un nuevo método de mallado para generar mallas tridimensionales estructuradas de dientes de engranaje que, al ser rápido y fácil de implementar, permita realizar refinamiento localizado de la malla y minimice la aparición de elementos distorsionados en la malla.

Definición del problema de mallado
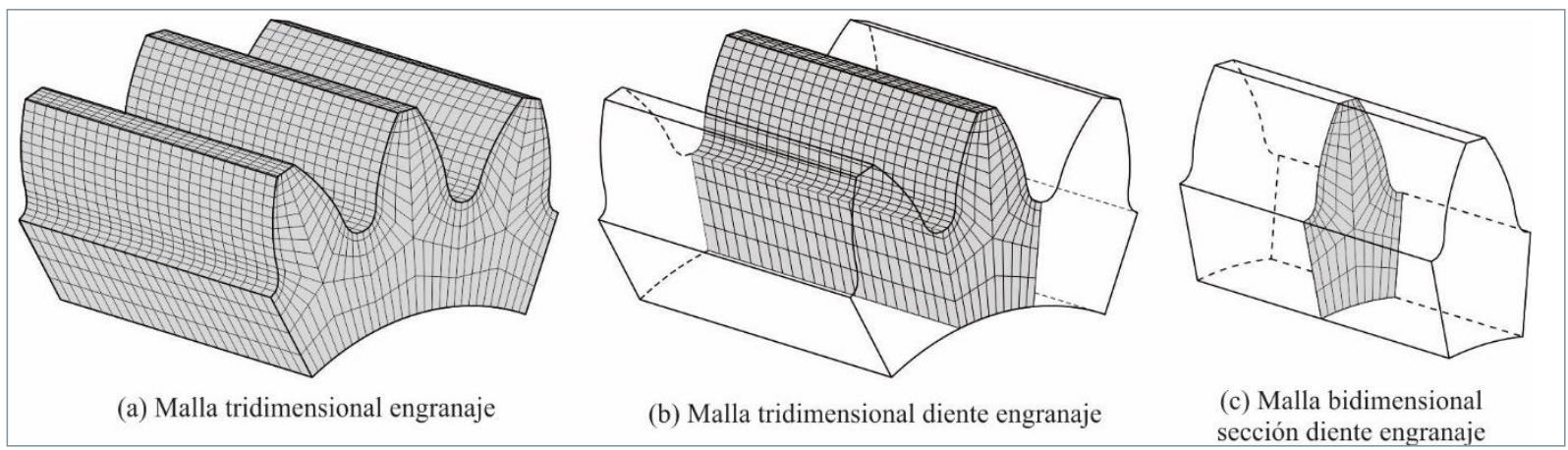
En este trabajo se trata el problema de la generación de una malla de elementos finitos hexaédricos sobre una geometría de engranaje, como la mostrada en la figura 1a. En general, dicha malla se puede construir mediante un patrón circular de una malla de elementos hexaédricos de uno de los dientes del engranaje (Fig. 1b). Al mismo tiempo, una malla de elementos hexaédricos de un diente del engranaje se puede obtener mediante un barrido, a lo largo de su ancho de cara, de una malla de elementos cuadrilateros extendida sobre la sección transversal del mismo (Fig. 1c). Por este motivo, se puede decir que el problema de generar una malla de elementos hexaédricos de un engranaje se puede reducir al problema de generar una malla de elementos cuadriláteros sobre la sección transversal de uno de sus dientes.

A partir de estas premisas, este trabajo sigue la estructura siguiente: en el apartado 3 se describe un método multibloque para generar mallas de cuadriláteros sobre secciones planas de engranajes [24]; más adelante, se describe, en primer lugar, la construcción de una malla de hexahedros de un diente de engranaje y, en segundo lugar, la generación de la malla para la geometría del engranaje.

Modelo multibloque para el mallado de secciones planas de engranajes
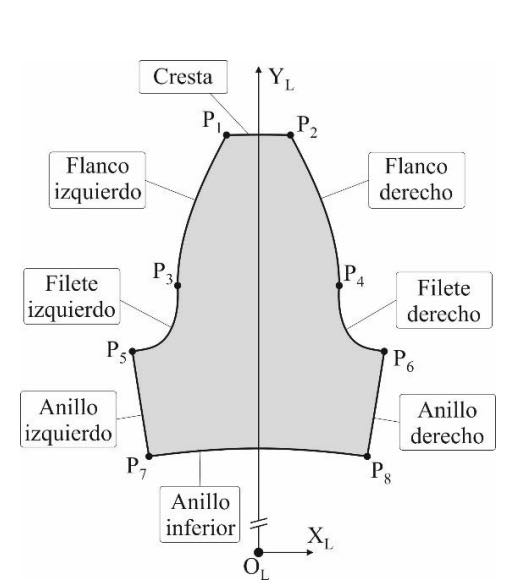
La figura 2 muestra una sección típica de un diente de engranaje. Este diente está definido respecto a un sistema de coordenadas local cuyo origen de coordenadas O_Lestá en el centro de la sección del engranaje, y su eje Z_L es normal al plano de la sección. El eje Y_L del sistema de referencia local está dispuesto de manera que el diente queda vertical y centrado sobre este eje.

La sección del diente está definida por ocho curvas paramétricas que se pueden determinar analíticamente utilizando las ecuaciones del perfil del diente y de las correspondientes porciones del anillo [8]. Los puntos de intersección entre dos curvas de contorno se denotan por P_i  {i=1,2,…,8}.

La generación de una malla de elementos cuadriláteros sobre la sección del diente es un problema difícil de resolver, debido a que es un dominio no convexo con un contorno complejo. En casos como este, se recomienda el uso de técnicas de mallado multibloque [25-27]; se pueden resumir en los pasos siguientes:

Paso 1. La sección del diente se descompone en un conjunto de geometrías simples, llamadas parches, de manera que la geometría de cada parche es apta para el esquema de mallado que se aplicará. La descomposición propuesta se describe más adelante.

Paso 2. Se especifican n_i + 1 semillas de mallado sobre cada una de las curvas de los parches. Estas semillas representan la posición que los nodos de la malla resultante ocuparán sobre ellas. Este paso se discute en profundidad más adelante.

Paso 3. Cada parche se malla, de manera independiente, utilizando un esquema de mallado local. En este trabajo, se propone la utilización del esquema de mallado propuesto por Miranda [28], que se basa en la interpolación transfinita [29] y se describe más adelante.

Cuando se han completado estos pasos, las mallas individuales obtenidas para cada parche se combinan para obtener la malla final. Habitualmente, este tipo de métodos de mallado da lugar a elementos distorsionados y, por ese motivo, se suelen completar con técnicas de optimización de la malla. En este trabajo, se sugiere la utilización de un método de suavizado de la malla, que se describe el apartado Suavizado de malla.

Descomposición de la sección del diente de engranaje
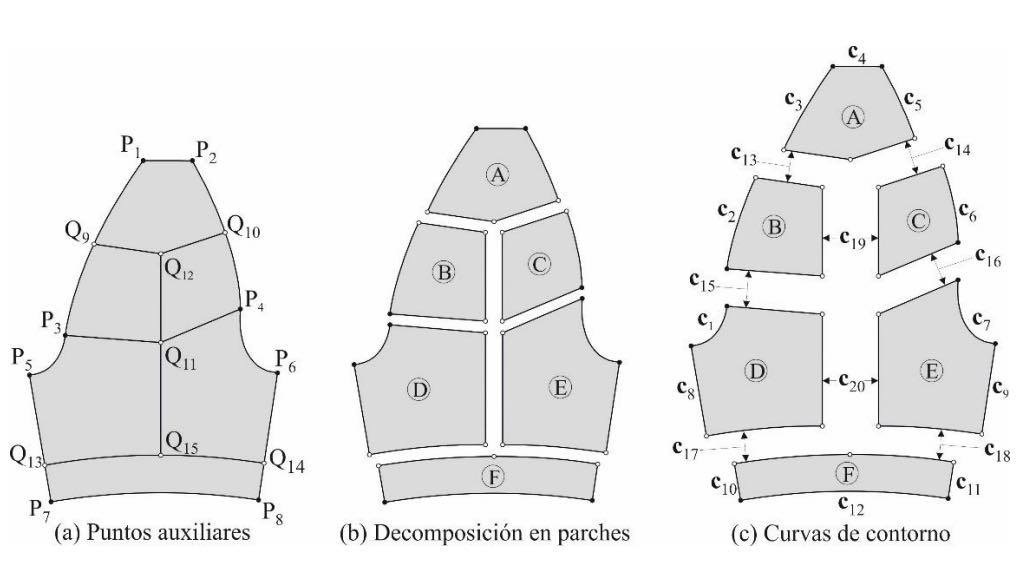
La descomposición propuesta para el diente de engranaje se muestra en la figura 3a. Esta descomposición está basada en la determinación de siete puntos auxiliares que se denotan por Q_i {i=9,10,…,15}. Cuando se conoce la posición de estos puntos, se trazan líneas entre ellos y los puntos existentes P_i que permiten dividir el diente en seis parches (A, B, C, D, E y F), como se muestra en la figura 3b. Finalmente, las curvas de contorno de los parches resultantes se renombran a c_i  {i=1,2,…,20}, como se indica en la figura 3c.

Para determinar la posición de los puntos auxiliares Q_i, se siguen los siguientes pasos:

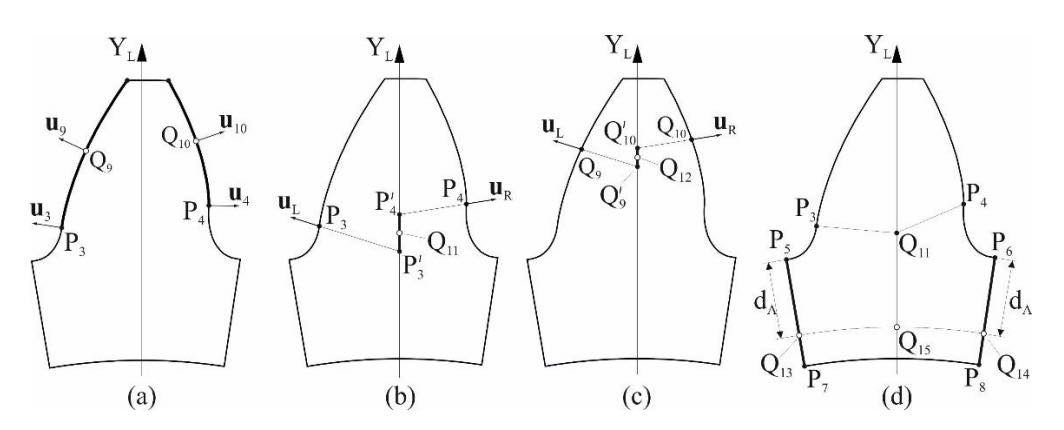
1. 1. Los puntos Q₉ y Q₁₀ se localizan sobre los flancos izquierdo y derecho (Fig. 1), respectivamente, de manera que dividen estas curvas en dos partes de igual longitud (Fig. 4a). Entonces, se determinan los vectores normales unitarios sobre los puntos P₃, P₄, Q₉ y Q₁₀ (y se denotan por u3 , u4, u9 y u10, respectivamente, como se indica en la figura 4a).
   2. Se calcula el vector uL como el bisector de los vectores u3 y u9 . De manera similar, se calcula el vector u8 como el bisector de los vectores u4 y u10.
   3. Como se muestra en la figura 4b, el punto P3 se proyecta sobre el eje YL siguiendo la dirección marcada por el vector uL para encontrar el punto P’3 , y el punto P4 se proyecta sobre el eje YL siguiendo la dirección marcada por el vector uR para encontrar el punto P’4 . Entonces, el punto Q11 se ubica en el punto intermedio del segmento que conecta los puntos P’3 y P’4 .
   4. De manera similar (Fig. 4c), el punto Q9 se proyecta sobre el eje YL siguiendo la dirección marcada por el vector uL para encontrar el punto Q’9 , y el punto Q10 se proyecta sobre el eje YL siguiendo la dirección marcada por el vector uR para encontrar el punto Q’10. Entonces, el punto Q12 se ubica en el punto intermedio del segmento que conecta los puntos Q’9 y Q’10.
   5. Se define la distanca dA como la media de las longitudes de los segmentos P3 Q11 y .P4 Q11
   6. El punto Q13 se ubica sobre el anillo izquierdo a una distancia dA del punto P5 , y el punto Q14 se ubica sobre el anillo derecho a la misma distancia dA del punto P6, como se muestra en la figura 4d.
   7. Finalmente, el punto Q15 se obtiene a partir de la intersección del eje YL y una circunferencia centrada en OL que pasa por los puntos Q13 y Q14 (Fig. 4d).

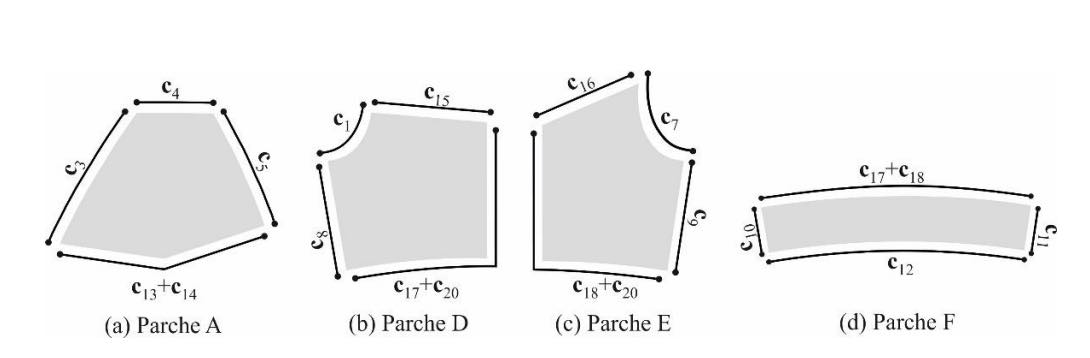
Para que los parches sean aptos para la aplicación de métodos de mallado basados en la interpolación transfinita, deben ser geometrías convexas, topológicamente equivalentes a un cuadrado definido por cuatro curvas de contorno. Sin embargo, como se observa en la figura 3c, los parches A, D, E y F están definidos por cinco curvas de contorno. Por tanto, será necesario necesario reducir el número de curvas de contorno en cada parche, uniendo dos curvas adyacentes. La combinación de curvas propuesta se muestra en la figura 5.

Discretización de las curvas de contorno
El método de mallado propuesto se desarrolla asumiendo que se proporciona una discretización de las curvas de contorno de los parches, en términos de ni + 1 semillas de mallado distribuidas a lo largo de las curvas de contorno c i , que las dividen en ni segmentos.

Sin embargo, antes de continuar con el proceso de mallado, es necesario comprobar que la discretización proporcionada es adecuada para el método local de malla que se aplicará sobre los parches. En general, cuando se desea mallar un parche con elementos cuadriláteros, se tiene que satisfacer que el número de total de divisiones en las curvas de contorno de un parche debe ser un número par. Considerando todos los parches en los que se ha descompuesto la sección del diente, este requisito se puede convertir en las seis condiciones matemáticas mostradas en la tabla 1.

Generación de mallas de elementos cuadrilateros sobre los parches
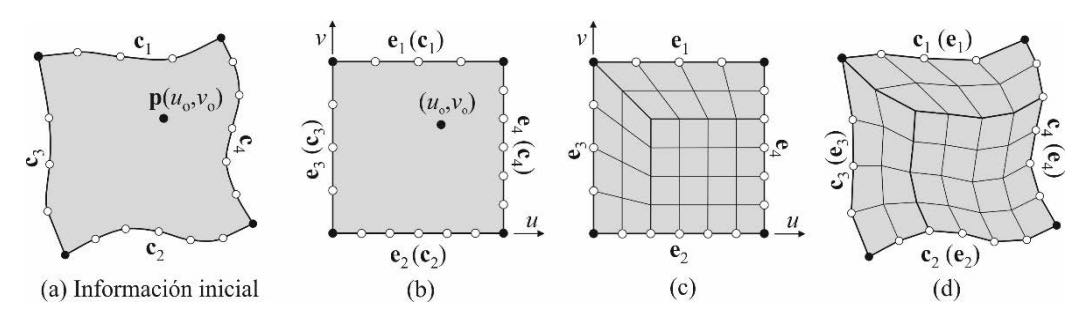
Una vez discretizadas las curvas de contorno de los parches, se puede proceder a su mallado. Para ilustrar este proceso, considérese un parche genérico como el mostrado en la figura 6a, que está definido por cuatro curvas paramétricas denotadas por c i {i=1,2,…,4}. Sobre cada una de estas curvas, hay distribuidos ni + 1 semillas de mallado, que la dividen en ni segmentos.

El proceso de generar una malla de cuadriláteros sobre dicho parche se puede resumir en tres pasos. En el primero de ellos, el parche se representa en el espacio lógico utilizando un cuadrado de referencia (Fig. 6b), de manera que cada arista del cuadrado de referencia (que se denotan ei {i=1,2,…,4}) corresponde con una de las curvas de contorno del parche. Las semillas de mallado distribuidas sobre las curvas de contorno también se representan sobre las aristas de este cuadrado de referencia.

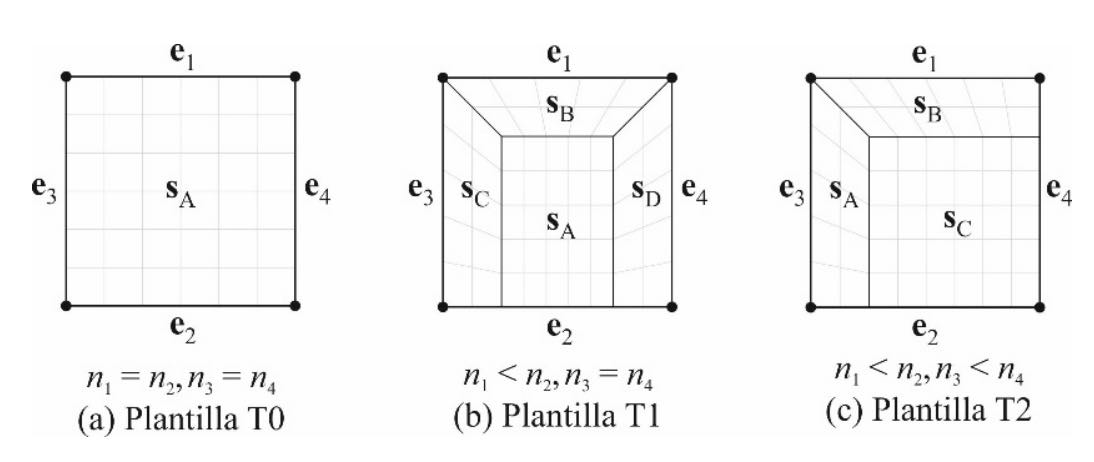
En el siguiente paso se genera una malla de cuadriláteros sobre el cuadrado de referencia (Fig. 6c). A tal efecto, se utiliza el método propuesto por Miranda [28], que está basado en la descomposición recursiva del dominio utilizando plantillas jerárquicas. Para ello, se utilizan las tres plantillas mostradas en la figura 7, cuya selección y orientación dependen del número de divisiones en cada una de las aristas del cuadrado de referencia:

• • La plantilla T0 se aplica cuando los aristas opuestas tienen el mismo número de divisiones (Fig. 7a). Esta plantilla genera una subregión(SA) que se puede mallar fácilmente con una interpolación bilinear.
  • La plantilla T1 se aplica cuando el número de divisiones de un par de aristas opuestas es igual, pero el número de divisiones en el otro par de aristas es distinto (Fig. 7b). Esta plantilla genera cuatro subregiones (s A, s B, sC, sD) en las que se puede aplicar la plantilla T0.
  • Finalmente, la plantila T2 se aplica cuando el número de divisiones en las aristas opuestas es distinto (Fig. 7c). La plantilla T2 genera tres subregiones (s A, s B, sC) . La plantilla T0 se aplica a las subregiones s A y s B . La subregión s C puede corresponder a una plantilla T0 o T1, dependiendo del número de divisiones en las aristas de dicha subregión.

Una vez aplicada la descomposición recursiva, se puede aplicar la plantilla T0 a todas las subregiones resultantes, y, por tanto, se puede mallar utilizando una interpolación bilinear. Para obtener la malla final, se combinan las mallas de todas las subregiones.

En el último paso del método de mallado local, la malla se transfiere del cuadrado de referencia en el espacio lógico al parche en el espacio físico utilizando interpolación transfinita [30] (Fig. 6d.).

Suavizado de la malla
Se sabe que la presencia de elementos distorsionados en la malla reduce la convergencia y la precisión de los análisis por el método de los elementos finitos [31]. Sin embargo, la mayoría de los métodos de mallado no pueden evitar la aparición de elementos distorsionados y, por este motivo, se suelen completar con técnicas de mejora de la malla. Tradicionalmente, las técnicas de mejora de la malla se clasifican en laplacianas y métodos basados en optimización. Aunque los primeros son más eficientes en términos computacionales, los segundos proporcionan mallas con menor distorsión.

En los métodos basados en optimización, la posición óptima de los nodos de la malla se determina resolviendo un problema de optimización, que puede ser local o global. En estos problemas de optimización las funciones objetivo son métricas de calidad de malla, que miden el grado de distorsión de los elementos de la malla. Hay un gran rango de métrica de calidad de malla que pueden ser utilizadas como funciones objetivo en los métodos basados en optimización. Entre ellas, la métrica propuesta por Oddy [32] ha demostrado ser particularmente efectiva para estos usos [33].

Como se ha comentado anteriormente, la optimización de la malla puede realizarse desde un punto de vista global o local. Aunque el método global [34] ha demostrado ser interesante para mallas con un número reducido de nodos, se vuelve poco apropiado para mallas con muchos nodos. Por esta razón, en este trabajo se ha optado por utilizar el método local de optimización [33].

En el método local, la posición de cada nodo interior se optimiza de manera independiente. La función objetivo es la suma de la métrica de Oddy de todos los elementos conectados al nodo cuya posición se está optimizando (es decir, depende de las variables xL e yL ). De esta manera, y siguiendo las ideas propuestas por Knupp [33], la optimización se realiza utilizando un esquema de Newton modificado. Este proceso se realiza para cada uno de los nodos de la malla y el proceso se repite hasta que se alcanza un criterio de convergencia dado.

Generación de mallas tridimensionales de engranajes
Como se ha ejemplificado en la figura 1, la generación de la malla de hexaedros de un engranaje se realiza mediante una matriz circular de las mallas hexaédricas de dientes de engranajes. Al mismo tiempo, una malla de hexaedros de un diente de engranaje se obtiene a partir del barrido, a lo largo de su ancho de cara, de una malla de cuadriláteros de una sección trasversal del diente.

Para la realización de dicho barrido, se genera un número determinado de secciones transversales a lo largo del ancho de cara del diente. Para cada una de estas secciones se genera una malla de cuadriláteros, utilizando el método descrito anteriormente. Es importante notar que todas las secciones deben ser topológicamente equivalentes y estar definidas por las curvas de contorno mostradas en la figura 2, aunque su geometría puede no ser igual.

Para asegurar que el espacio que queda entre las mallas de elementos cuadriláteros de dos secciones adyacentes se pueda rellenar con elementos hexaédricos, es importante que ambas mallas sean topológicamente equivalentes, es decir, es necesario que la disposición de los nodos y las incidencias de los elementos sean similares de manera que los elementos cuadriláteros de una sección se puedan conectar con los elementos cuadriláteros de la sección contigua. Para ello, es importante que los parches equivalentes de ambas secciones se mallen utilizando la misma plantilla de mallado, con el mismo número de divisiones en sus curvas de contorno. Cumpliendo estas directrices, la generación de la malla tridimensional de hexaedros resulta trivial.

Ejemplos numéricos
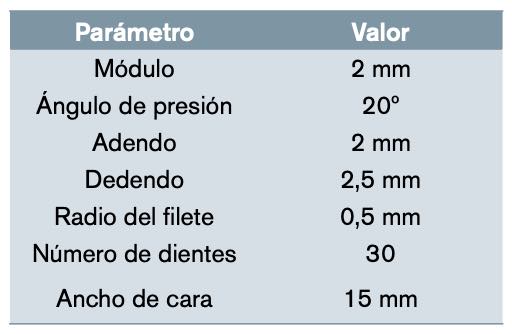
El funcionamiento del método de mallado descrito se ilustra mediante el desarrollo y análisis de un modelo de elementos finitos de una transmisión de engranajes cilíndricos rectos denominado modelo propuesto. La transmisión seleccionada para el ejemplo consiste en dos engranajes cilíndricos con perfil de evolvente, que están perfectamente alineados, y cuya geometría se define por los parámetros de la tabla 2.

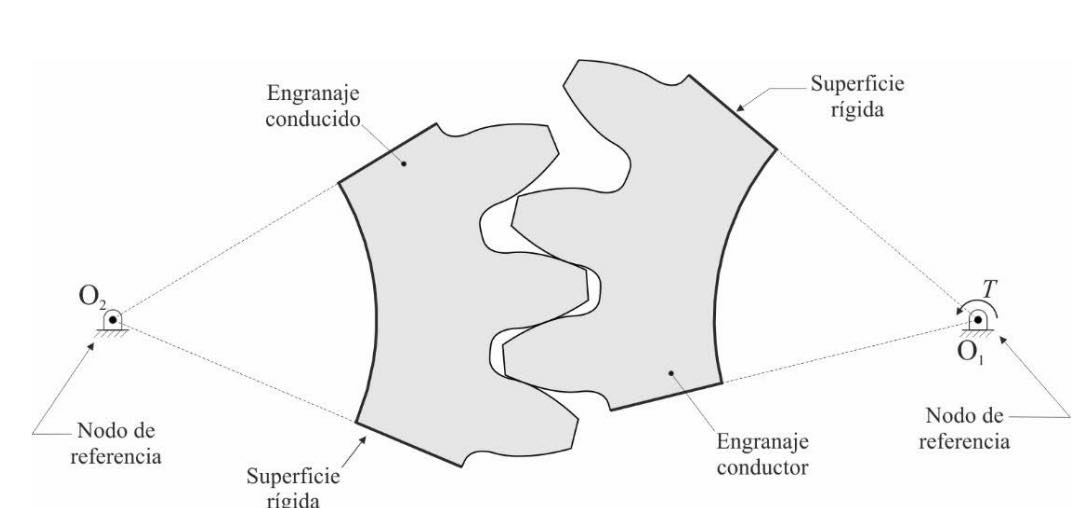
La figura 8 muestra un modelo de elementos finitos típico de una transmisión de engranajes que está compuesto por las geometrías del engranaje conductor y el conducido, que pueden consistir en uno o distintos dientes. Sobre el anillo de los engranajes se define una arista rígida, cuyos movimientos están acoplados a los de unos nodos de referencia que coinciden con el eje de rotación de los engranajes.

Las condiciones de contorno se definen sobre estos nodos de referencia, que tienen todas las traslaciones restringidas, así como los giros en las direcciones perpendiculares al eje de rotación del engranaje. Sobre el nodo de referencia del engranaje conductor se define un par torsor T = 120 Nm, y la rotación del sistema se restringe definiendo un valor constante para el grado de libertad de rotación del nodo de referencia del engranaje conducido. Se considera que el material de los engranajes es elástico lineal, con un módulo de elasticidad de 210 GPa y un coeficiente de Poisson de 0,3.

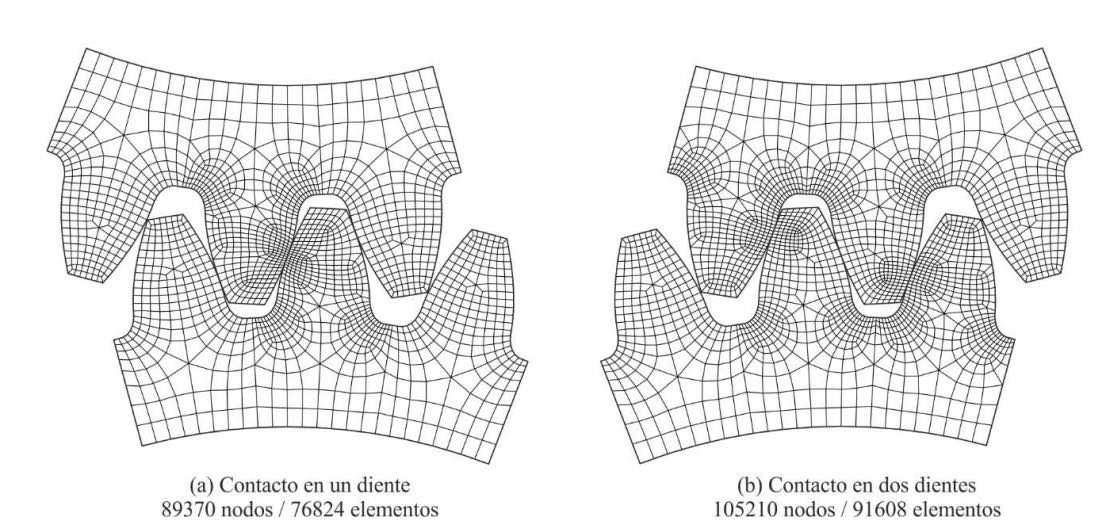
El modelo de elementos finitos se analiza para dos posiciones de contacto distintas. En la primera de ellas hay un único diente en contacto, mientras que en la segunda hay dos dientes que contactan simultáneamente. La figura 9 muestra las mallas generadas para cada uno de los dos casos, observadas en el plano normal de la transmisión. Estas mallas se han generado considerando 45 secciones distribuidas uniformemente por todo el ancho de cara de los engranajes.

Como se puede observar en la figura 9, el método de mallado desarrollado permite obtener un refinamiento local de la malla en las zonas en las que se produce el contacto entre dientes, así como en los filetes de los dientes que soportan la carga. Estas zonas son las que habitualmente están expuestas a un mayor gradiente de tensiones y, en consecuencia, las que requieren de un mallado más fino para aumentar la precisión del análisis. Además, el refinamiento en la zona en la que se produce el contacto es muy importante para describir con precisión la geometría de la superficie del engranaje.

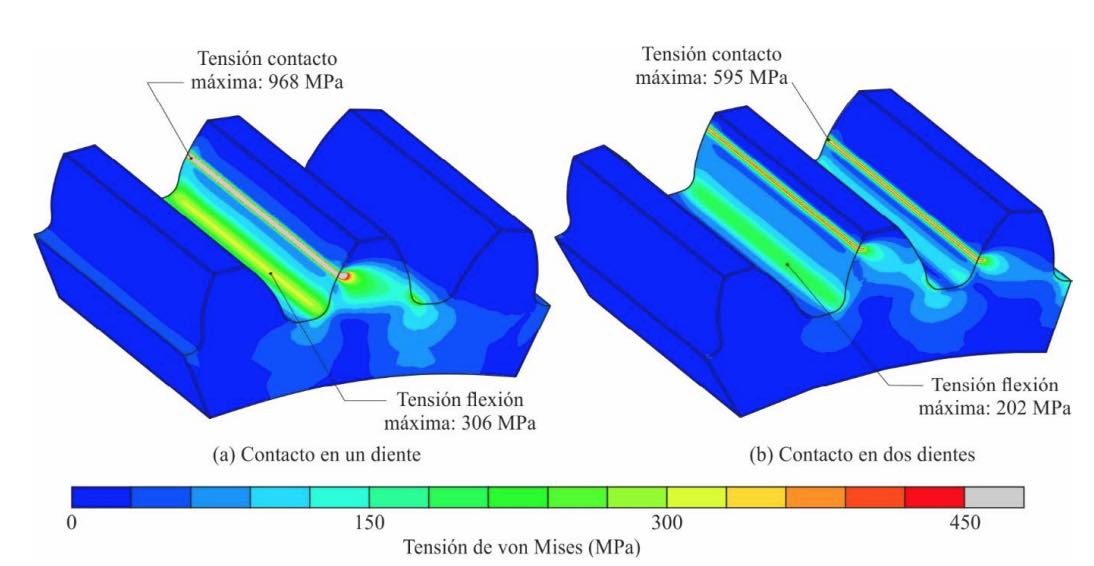
La figura 10 muestra la distribución de tensiones de Von Mises a lo largo de la geometría del engranaje conductor, obtenida a partir del análisis del modelo de elementos finitos utilizando ABAQUS [35]. Como era de esperar, las tensiones más elevadas se producen en las zonas cercanas al contacto entre dientes. Asimismo, también se producen tensiones elevadas en las zonas de los filetes, que son mayores en el filete que trabaja a compresión que en el filete que trabaja a tracción.

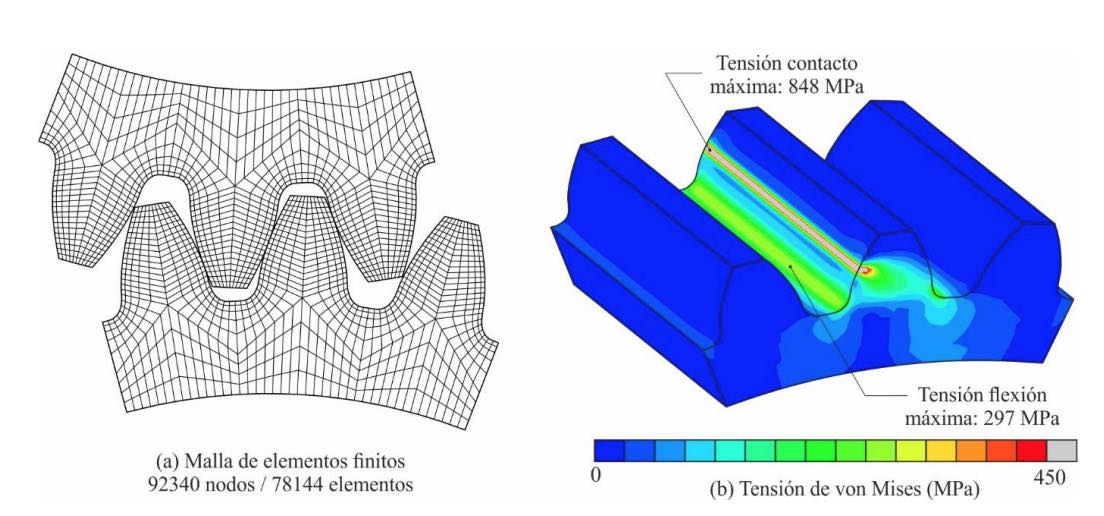
A efectos de comparación, se ha desarrollado otro modelo de elementos finitos, denominado modelo de comparación, en el que el mallado de las geometrías de los engranajes se ha realizado utilizando la metodología propuesta por Argyris [12]. El modelo se estudia en la posición en la que el contacto se produce entre una única pareja de dientes y la malla de elementos finitos obtenida, como se muestra en la figura 11a. En este caso, se ha intentado que el tamaño del modelo, en términos del número de nodos y número de elementos, sea similar al modelo mostrado en la figura 9a. De esta manera, la comparación entre ambos modelos se puede establecer en términos de precisión de sus resultados, puesto que el coste computacional será similar en ambos casos.

La Figura 11b muestra la distribución de tensiones de Von Mises determinada a partir del análisis del modelo de comparación mediante ABAQUS. Como se puede observar, los valores máximos de tensión de Von Mises siguen apareciendo en la zona en la que se produce el contacto entre dientes, pero en este caso su valor es un 13% inferior al modelo propuesto. Las tensiones de flexión también presentan un valor máximo que es ligeramente inferior al obtenido en el modelo propuesto.

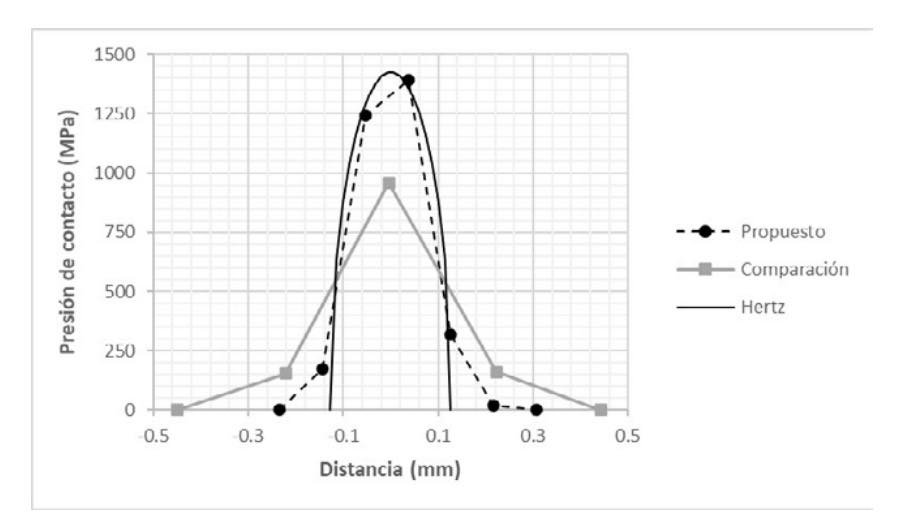
Finalmente, la figura 12 muestra la distribución de presiones de contacto obtenida a partir de los dos modelos. Asimismo, también se muestra la distribución de presiones de contacto obtenida analíticamente a partir de la teoría de contacto de Hertz [36]. Como se puede observar, la distribución de presiones de contacto obtenida a partir del modelo propuesto se aproxima en mayor medida a la distribución teórica que la obtenida a partir del modelo de comparación.

Conclusiones
En este trabajo se ha desarrollado un nuevo método para la generación automatizada de mallas tridimensionales de engranajes. El método propuesto se basa en la utilización de un método multibloque para generar una malla de cuadriláteros sobre una sección plana del engranaje que, posteriormente, se extruye por todo su ancho de cara para generar una malla tridimensional de hexaedros.

El funcionamiento del método propuesto se ha ilustrado con ejemplos numéricos que demuestran su capacidad para generar mallas con refinamiento local y reducido nivel de distorsión. La comparación con otros métodos de mallado existentes muestra la capacidad del método propuesto para optimizar la posición de los nodos de la malla de cara a maximizar la precisión de los resultados.

Agradecimientos
Los autores agradecen a la Universitat Jaume I el apoyo económico del proyecto UJI-A2019-24.

---

Referencias

[1] Hotait M. A., Kahraman A., Nishino T. “An investigation of root stresses of hypoid gears with misalignments”, J. Mech. Des. Trans. ASME 133, (2011).

[2] Hasl C., Liu H., Oster P., Tobie T., Stahl, Forschungsstelle fuer Zahnraeder und Getriebebau (Gear Research Centre). “Method for calculating the tooth root stress of plastic spur gears meshing with steel gears under consideration of deflection-induced load sharing”, Mech. Mach. Theory 111, 152-163 (2017).

[3] Mao K. “Gear tooth contact analysis and its application in the reduction of fatigue wear”, Wear 11, 1281-1288 (2007).

[4] Gonzalez-Perez I., Sanchez-Marin F., RodaCasanova V., Fuentes A., Iserte J. L. “A Finite Element Model for Consideration of the Torsional Effect on the Bearing Contact of Gear Drives”, J. Mech. Des. 134 (2012).

[5] Patil S. S., Karuppanan S., Atanasovska I., Wahab A.A. “Contact stress analysis of helical gear pairs, including frictional coefficients”, Int. J. Mech. Sci.85, 205-211 (2014).

[6] Roda-Casanova V., Sanchez-Marin F. “A 2D finite element based approach to predict the temperature field in polymer spur gear transmissions”, Mech. Mach. Theory 133, 195.210 (2019).

[7] Fernandes C.M.C.G., Rocha D.M.P., Martins R.C., Magalhães L., Seabra J.H.O. “Finite element method model to predict bulk and flash temperatures on polymer gears”, Tribol. Int. 120, 255-268 (2018)

[8] Litvin F. L., Fuentes A. Gear Geometry and Applied Theory, Cambridge University Press (2004).

[9] Barone S., Borgianni L., Forte P. “Evaluation of the effect of misalignment and profile modification in face gear drive by a finite element meshing simulation”, J. Mech. Des. Trans. ASME 126, 916-924 (2004).

[10] Ding H., Wan Z., Zhou Y., Tang J. “A data-driven programming of the human-computer interactions for modeling a collaborative manufacturing system of hypoid gears by considering both geometric and physical performances”, Robot. Comput. Integr. Manuf. 51, 121-138 (2018).

[11] Karpat F., Ekwaro-Osire S., Cavdar K., Babalik F.C. “Dynamic analysis of involute spur gears with asymmetric teeth”, Int. J. Mech. Sci. 50, 1598- 1610 (2008).

[12] Argyris J., Fuentes A., Litvin F.L. “Computerized integrated approach for design and stress analysis of spiral bevel gears” , Comput. Methods Appl. Mech. Eng. 191, 1057-1095 (2002).

[13] Iñurritegui Marroquin A., Arana A., Hernández Jiménez M., Elizegi J., Ulacia I., Larranaga J. “2D modeling of cylindrical gears by the finite element method”, Actas del XXII Congreso Nacional de Ingeniería Mecánica, Madrid (2018).

[14] Pedrero J.I., Pleguezuelos M., Artés M., Antona J.A. “Load distribution model along the line of contact for involute external gears”, Mech. Mach. Theory 45, 780-794 (2010).

[15] Zanzi C., Pedrero J. I. “Application of modified geometry of face gear drive”, Comput. Methods Appl. Mech. Eng. 195, 3047-3066 (2005).

[16] Cappellini N., Tamarozzi T., Blockmans B., Fiszer J., Cosco F., Desmet W. “Semi-analytic contact technique in a non-linear parametric model order reduction method for gear simulations”, Meccanica, (2018).

[17] Knupp P. M. “Remarks on Mesh Quality”, 45th AIAA Aerosp. Sci. Meet. Exhib., 2-5 (2007).

[18] Gonzalez-Perez I., Fuentes-Aznar A. “Implementation of a finite element model for stress analysis of gear drives based on multipoint constraints”, Mech. Mach. Theory 117, 35- 47 (2017).

[19] Barbieri M., Zippo A., Pellicano F. “Adaptive gridsize finite element modeling of helical gear pairs”, Mech. Mach. Theory 82, 17-32 (2014).

[20] Liu Y., Zhao Y., Liu M., Sun X. “Parameterized High-Precision Finite Element Modelling Method of 3D Helical Gears with Contact Zone Refinement”, Shock Vib. 2019, 1–17 (2019).

[21] Gonzalez-Perez I., Fuentes-Aznar A. “Implementation of a Finite Element Model for Gear Stress Analysis Based on Tie-Surface Constraints and Its Validation Through the Hertz’s Theory”, J. Mech. Des. Trans. ASME 140, (2018).

[22] Roarty C. M., Grosland N. M. “Adaptive meshing technique applied to an orthopaedic finite element contact problem.” , Iowa Orthop. J. 24, 9-21 (2004).

[23] Keskin A. “On the quantification of errors of a pre-processing effort reducing contact meshing approach”, 53rd AIAA Aerospace Sciences Meeting, Virginia (2015).

[24] Roda-Casanova V., Sanchez-Marin F. “Development of a multiblock procedure for automated generation of two-dimensional quadrilateral meshes of gear drives”, Mech. Mach. Theory. 143, (2020).

[25] Frey P. J., George P. L. Mesh Generation: Application to Finite Elements: Second Edition, Wiley-ISTE (2010).

[26] Owen S. “A survey of unstructured mesh generation technology”, 7th Int. Meshing Roundtable, (1998).

[27] Farrashkhalvat M., Miles J. P. Basic Structured Grid Generation: With an introduction to unstructured grid generation, ButterworthHeinemann (2003).

[28] de Oliveira Miranda A. C., Martha L. F. “Hierarchical template-based quadrilateral mesh generation”, Eng. Comput. 33, 701-715 (2017).

[29] Nguyen H. L. “On the applications of algebraic grid generation methods based on trans nite interpolation”, Cleveland (1989).

[30] Gordon W. J., Hall C. A. “Construction of curvilinear co?ordinate systems and applications to mesh generation”, Int. J. Numer. Methods Eng. 7, 461-477 (1973).

[31] Lee N.S., Bathe K.J. “Effects of element distortions on the performance of isoparametric elements”, Int. J. Numer. Methods Eng. 36, 3553- 3576 (1993).

[32] Oddy A., Goldak J., McDill M., Bibby M. “Distortion metric for isoparametric finite elements”, Trans. Can. Soc. Mech. Eng. 12, 213-217 (1988).

[33] Knupp P. M. “Achieving finite element mesh quality via optimization of the Jacobian matrix norm and associated quantities. Part I – A framework for surface mesh optimization”, Int. J. Numer. Methods Eng. 48, 401-420 (2000).

[34] Canann S. A. Stephenson M. B., Blacker T., “Optismoothing: An optimization-driven approach to mesh smoothing” , Finite Elem. Anal. Des. 13, 185-190 (1993).

[35] Abaqus Analysis User’s Guide, Dassault Systèmes (2014). [36] Johnson K. L. Contact Mechanics, Cambridge University Press (1989).