Análisis del curado dual en resinas epoxi mediante un molde instrumentado
Analysis of dual curing in epoxy resins using an instrumented mold
Albert Fabregat-Sanjuan (1), Xavier Fernández-Francos (2), Francesc Ferrando-Piera (1)
Resumen
En las tecnologías de procesado utilizadas en la fabricación de materiales compuestos termoestables es clave controlar la velocidad de reacción y la exotermicidad del proceso para minimizar la aparición de tensiones internas que acaban originando la aparición de defectos mecánicos y dimensionales, especialmente cuando tienen un cierto grosor. Para mejorar este comportamiento se ha propuesto el uso de sistemas de curado dual secuenciales con control cinético-térmico. De este modo, se pretende limitar el avance de la reacción hasta un estadio intermedio uniforme y estable a partir del cual el curado pueda tener lugar de manera más controlable, minimizando gradientes de conversión y térmicos durante la etapa de entrecruzamiento y, por tanto, reduciendo la formación de tensiones internas y posibles defectos. En este trabajo se muestran los resultados de la validación experimental de este concepto. Los resultados experimentales obtenidos han validado la simulación de la reacción química y su exotermicidad. También han permitido analizar el efecto en el proceso de curado que tienen las fibras de refuerzo utilizadas habitualmente con las resinas analizadas.
Palabras clave: Materiales compuestos, cinética, curado dual, propiedades térmicas, termoestables
Abstract
In the processing technologies used in the manufacture of thermosetting composite materials, it is key to control the reaction rate and the exothermicity to minimize the appearance of internal stresses that end up causing mechanical and dimensional defects, especially when they have a certain thickness. To improve this behaviour, the use of sequential dual curing systems with kinetic-thermal control has been proposed. In this way, it is intended to limit the progress of the reaction to a uniform and stable intermediate stage from which curing can take place in a more controllable way. Moreover, conversion and thermal gradients are minimized during the crosslinking stage and, therefore, the formation of internal stresses and possible defects are reduced. This paper shows the results of the experimental validation of this concept. The experimental results obtained have validated the simulation of the chemical reaction and its exothermicity. They have also made it possible to analyze the effect on the curing process of the reinforcing fibers commonly used with the analyzed resins.
Keywords: Composites, kinetics, dual curing, thermal properties, thermosets
Recibido / received: 20/06/2021. Aceptado / accepted: 24/10/2021.
1 Departamento de Ingeniería Mecánica, Universitat Rovira i Virgili
2 Departamento de Máquinas y Motores Térmicos, Universitat Politècnica de Catalunya;
Autores para correspondencia: Albert Fabregat: a.fabregat@urv.cat; Xavier Fernández: xavier.fernandez@upc.edu; Francesc Ferrando: f.ferrando@urv.cat
Introducción
En las tecnologías de procesado utilizadas en la fabricación de materiales compuestos termoestables es clave controlar la velocidad de reacción y la exotermicidad del proceso. La exotermicidad del proceso puede generar importantes gradientes térmicos y de conversión. Estos gradientes y la contracción química/ térmica de las resinas durante el curado implican la aparición de tensiones internas que acaban provocando la aparición de defectos mecánicos y dimensionales, especialmente cuando tienen un cierto grosor [1,2]. Para mejorar este comportamiento se ha propuesto el uso de sistemas de curado dual secuenciales con control cinético-térmico [3,4]. De este modo, se pretende limitar el avance de la reacción hasta un estadio intermedio uniforme y estable, a partir del cual el curado pueda tener lugar de manera más controlable, minimizando gradientes de conversión y térmicos durante la etapa de entrecruzamiento y, por tanto, reduciendo la formación de tensiones internas y posibles defectos.
La contracción inducida térmica y químicamente durante el procesamiento, en especial una vez que el material se ha gelificado y, por tanto, está desarrollando resistencia mecánica, es el principal responsable de los defectos. Si la temperatura alcanzada en el interior es demasiado alta, la degradación térmica podría ocurrir. El control de la temperatura y los perfiles de conversión se pueden lograr mediante la definición de programas de temperatura complejos que involucran una serie de pasos de perfiles de conversión uniformes o funciones de objetivos múltiples que incluyen múltiples efectos, como los cálculos de tensión interna [6]. Las formulaciones de termoestables de curado dual que combinan diferentes reacciones de polimerización son una alternativa interesante a los sistemas de curado convencionales debido a la posibilidad de controlar la secuencia de curado, el grado de curado en la etapa intermedia y la estructura y propiedades de la red intermedia y final [7]. Esto se logra mediante la elección de iniciadores y/o disparadores selectivos para cada reacción y simplemente cambiando la composición y estructura de los monómeros que participan en cada reacción. Estas características son atractivas para una serie de aplicaciones avanzadas, pero el control de la secuencia de curado también es valioso para diferentes escenarios de procesamiento, como el procesamiento de etapas múltiples o el curado de piezas compuestas de gran ventaja con respecto a las formulaciones convencionales que deben controlarse estrictamente en términos de tiempo de procesamiento-temperatura para obtener la estructura parcialmente curada deseada y, en consecuencia, garantizar una aplicación exitosa [8].
Para la validación experimental de este concepto este grupo de investigación realizó previamente el diseño y la instrumentación de un molde calefactable, con el que se pueden programar procesos de curado por etapas y en el que se monitoriza la temperatura de la parte superior e inferior del molde mediante dos sensores RTD y la temperatura de la resina mediante un sensor NTC. Además, el molde permite añadir fibras de refuerzo y variar el espesor de las probetas obtenidas y así analizar la influencia de las fibras de refuerzo y el espesor en los resultados [9].
En este artículo se utiliza una resina epoxi comercial de curado lento (IN2 Epoxy Infusion Resin) de Easy Composites [10] y una fórmula de doble curación (EBL70/S4). Se basa en diglicidil éter de bisfenol A (DG) y trimetilolpropano tris (3-mercaptopropionato) (S3) con un exceso de grupos epoxi, usando 1-metilimidazol (1MI) como iniciador aniónico. El procesamiento de piezas compuestas basado en este sistema se simuló mediante un método de diferencias finitas asumiendo la transferencia de calor bidimensional con simetría cilíndrica. La cinética de curado y las propiedades termofísicas del sistema de curado dual se determinaron experimentalmente, mientras que se usaron modelos adecuados para determinar las propiedades efectivas de las piezas compuestas.
La principal aplicación de estas resinas es la fabricación de componentes mediante VRTM o RTM Light (Vacuum Resin Transfer Moulding). Comparado con el proceso RTM clásico, el proceso VRTM o RTM Light es relativamente ligero (de ahí su nombre) y de un coste considerablemente menor. El proceso aprovecha la presión de vacío como ayuda al cierre del molde, a diferencia de los pesados sistemas de cierre usados en RTM. Un ejemplo de piezas fabricadas por este proceso son las palas eólicas y la mayoría de piezas para aviones y náutica.
Los resultados experimentales obtenidos han validado la simulación de la reacción química y su exotermicidad. La comparación entre los resultados experimentales y la simulación ha permitido validar las hipótesis simplificadoras planteadas en la simulación: 1) la geometría del modelo de simulación (sin elementos singulares como los tornillos de unión entre las placas del molde, las juntas tóricas y la vaselina utilizada para la estanqueidad de vacío y los racores y tubos de entrada y salida del fluido); 2) la diferencia entre los resultados concretos de temperatura en la simulación y la medición con sondas que, aunque de tamaño reducido no son puntuales y están encapsuladas en acero inoxidable, y 3) pequeños cambios en la temperatura ambiente experimental respecto a la hipótesis en la simulación de temperatura ambiente constante. Así pues, se ha demostrado que el proceso de reticulación se puede controlar fácilmente si el calor liberado durante la primera reacción se disipa correctamente, de modo que no se produzca un incremento de temperatura que conduzca a la activación prematura de la segunda reacción. Los resultados muestran que esta disipación se puede lograr mediante la selección de una temperatura y un tiempo de permanencia adecuados del primer curado, con el objetivo de evitar una gelificación prematura. El calentamiento posterior conduce a la activación de la segunda reacción y la reticulación, que tiene lugar de una manera más controlada debido a la reducida exotermicidad restante del segundo proceso de reacción. Los resultados también han permitido analizar el efecto en el proceso de curado que tienen las fibras de refuerzo utilizadas habitualmente con las resinas analizadas.
Materiales y métodos
En esta sección se presentan el material y los métodos utilizados. Para una mayor claridad se ha separado en diferentes apartados.
Equipo experimental
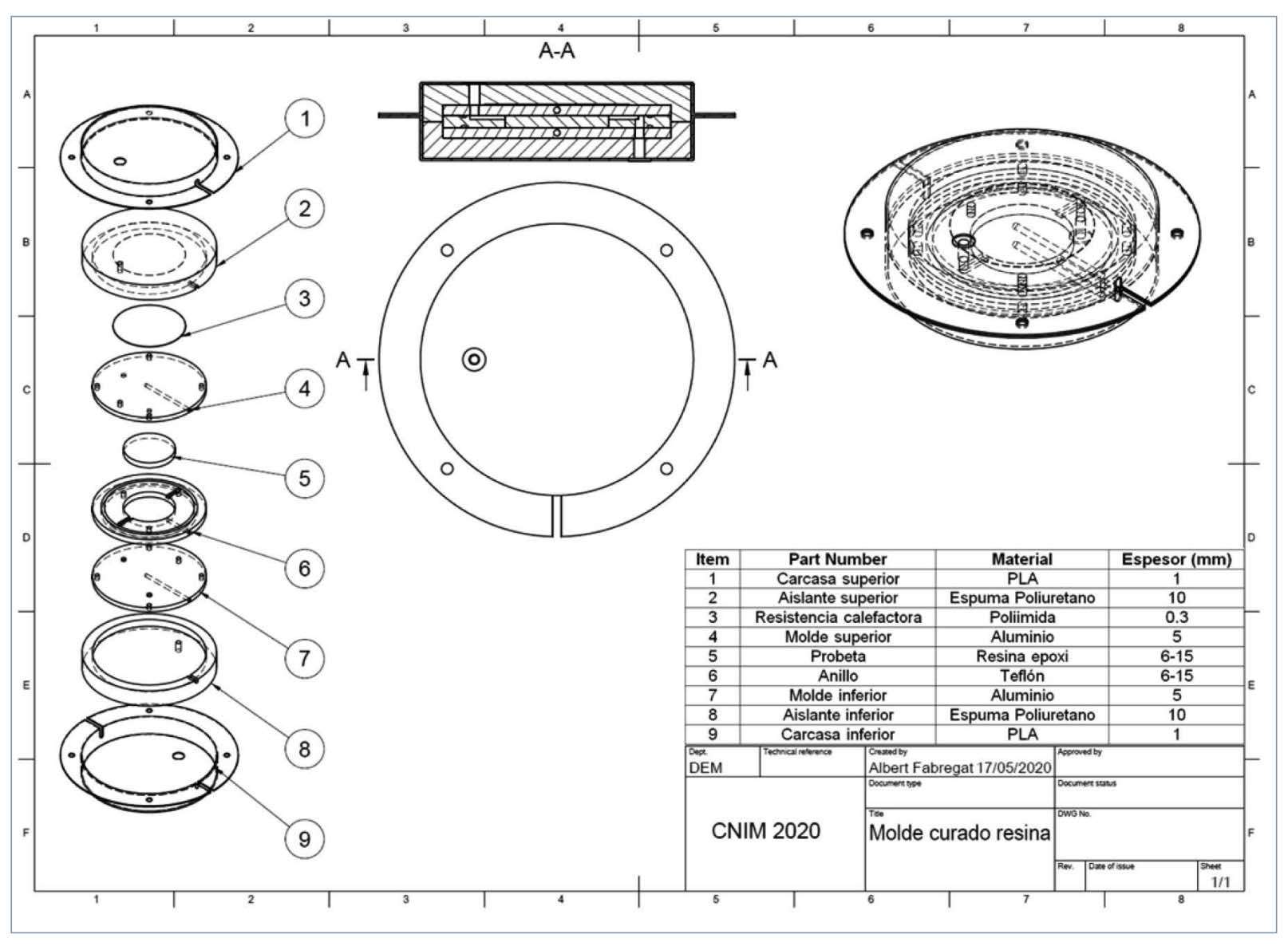
En la figura 1 se muestra el molde utilizado. La descripción completa del molde se puede consultar en Fabregat-Sanjuan et al. [9]. A continuación, se exponen las características más importantes. El molde es autocalefactable mediante control proporcional integrador derivativo (PID), con el que se pueden programar las etapas del curado dual y en el que se monitoriza la temperatura de la parte superior e inferior del molde mediante dos sensores de temperatura RTD (Resistance Temperature Detector) PT1000 y la temperatura de la resina mediante un sensor de temperatura NTC (Negative Temperature Coefficient). Además, el molde permite variar el espesor y utilizar fibras de refuerzo de las probetas obtenidas y así analizar la influencia del espesor y las fibras en los resultados.
Antes de introducir la resina en el molde se realizó la preparación de la mezcla. En el caso de la resina IN2 Epoxy, se realizó la mezcla de la resina y el endurecedor a temperatura ambiente (25 ºC), se mezcló con espátula durante 5 minutos y se realizó una desgasificación en vacío durante 15 minutos. Posteriormente, se realizó el vacío en el molde y se introdujo la resina. En el caso de la resina EBL70/S4 se realizó una etapa previa (un día antes del experimento) de mezcla de los componentes EBL70/S4 con espátula durante 5 minutos y desgasificación a 50 ºC durante 2 horas. Para terminar la preparación, en el momento del experimento se añade el iniciador mediante una mezcla con espátula de 5 minutos, seguido de una desgasificación en vacío a temperatura ambiente de 15 minutos. De la misma manera que con la resina IN2 epoxy, para suministrar la resina se realiza el vacío en el molde y se introduce la resina.
En el caso de las muestras preparadas con fibra, el proceso de preparación fue similar con la salvedad de que la fibra se introdujo en el molde antes de la infusión de la resina. La fracción en volumen de fibra se estimó a partir de las densidades de la resina y la fibra y la dimensión y masa de la muestra.
Materiales
La resina IN2 Epoxy es una resina epoxi-amina bicomponente para infusión con baja viscosidad (200-450 MPa·s a 25 ºC), lo que garantiza que pueda usarse con fibra de refuerzo. La resina ha sido suministrada por Easy Composites [10]. Los componentes A (amina) y E (epoxi) de la formulación se mezclan en una proporción másica de 30 a 100, respectivamente.
La resina EBL70/S4 consta del componente epoxi EBL70 (diglicidil éter de bisfenol A 185 g/eq, suministrado por Stera Chemicals), un politiol como agente de entrecruzamiento S4 (tetrakis[3-mercaptopropionato] de pentaeritritol, 489 g/mol, suministrado por Sigma-Aldrich) y el iniciador 1MI (1-metilimidazol 82 g/mol, suministrado por Sigma-Aldrich). La mezcla EBL70/S4 se prepara mezclando una relación másica de 77,2 a 22,8 en EBL70 y S4, respectivamente. Esta mezcla corresponde a una relación molar de grupos tiol a epoxi de 0,45:1, aproximadamente. A la mezcla se añade el 1% de 1MI.
La fibra de vidrio de refuerzo utilizada es de 600 g/m2 y de tipo Mat (largos hilos cortados colocados al azar que se mantienen cohesionados gracias a un emulsionante). Ha sido suministrada por la empresa Feroca SA [11]. El teflón utilizado para el anillo es estándar y la espuma de poliuretano para el aislante es de tipo ignifugo y tiene una densidad de 28 kg/m3 ; ambos materiales han sido suministrados por la empresa Industria de la Goma SA. El aluminio para la placa superior e inferior del molde es de la aleación EN AW 2024 y ha sido suministrado por la empresa Broncesval S.L.
Caracterización termofísica de las resinas
Se ha analizado la cinética de curado y se han determinado las propiedades térmicas de las distintas resinas mediante calorimetría diferencial de barrido (DSC). Se ha utilizado un equipo Mettler DSC 3+ equipado con un intracooler y DSC822 equipado con un brazo robótico para muestreo automático y enfriado mediante nitrógeno líquido. Ambos equipos han sido calibrados con patrones de indio y cinc.
La cinética de curado del sistema IN2 se ha analizado mediante análisis dinámicos a velocidades de calentamiento b comprendidas entre 1,25 y 20 ºC/min, y en condiciones isotérmicas a temperaturas T entre 60 ºC y 120 ºC. En el caso de la formulación EBL70/S4 la cinética de las dos etapas de curado se ha analizado de manera independiente. El primer proceso de curado del sistema EBL70/S4 se ha analizado a b entre 1,25 y 20 ºC/min y T entre 20 y 80 ºC. El segundo proceso de curado del sistema EBL70/S4 se ha analizado después de un primer curado a 80 ºC durante 5 minutos para completar la primera etapa, a velocidades de calentamiento b entre 1,25 y 10 ºC/min y T entre 90 y 130 ºC. El grado de conversión x y la velocidad de reacción dx/dt se han determinado mediante las siguientes expresiones:
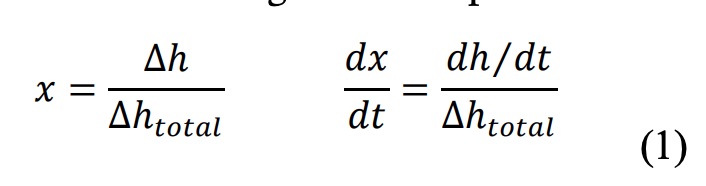 Donde ?h es el calor liberado hasta un cierto instante (experimento isotérmico) o temperatura (experimento dinámico), dh/dt es el flujo de calor liberado de manera instantánea, y ?htotal corresponde al calor total liberado en el proceso de curado en los experimentos dinámicos e isotérmicos, asumiendo que el curado sea completo en cualquier caso.
Donde ?h es el calor liberado hasta un cierto instante (experimento isotérmico) o temperatura (experimento dinámico), dh/dt es el flujo de calor liberado de manera instantánea, y ?htotal corresponde al calor total liberado en el proceso de curado en los experimentos dinámicos e isotérmicos, asumiendo que el curado sea completo en cualquier caso.
Para la determinación de la c p se ha empleado el método DIN 51007 utilizando alúmina (Al2 O3 ) como sustancia de referencia [12].
La densidad ? de las muestras se ha supuesto constante y se ha determinado a partir de una regla simple de mezcla y teniendo en cuenta la densidad de los componentes individuales de la formulación. La conductividad térmica l de las resinas curadas no ha sido medida y se han utilizado valores típicos de materiales similares en la literatura especializada [3,13].
La temperatura de transición vítrea Tg se determinó a una velocidad de calentamiento de 10 ºC/min como el punto medio en el salto de capacidad calorífica ?c p durante la relajación vítrea. Se hicieron determinaciones antes del proceso de curado (Tg0 y ?c p0) y después del proceso de curado (Tg0 y ?c p?). Se determinó la evolución de la Tg con el grado de curado, su relación Tg (x), a partir de la relación de Venditti y Gillham [14] con el fin de validar el modelo de propiedades termofísicas empleado en la simulación del proceso de curado.
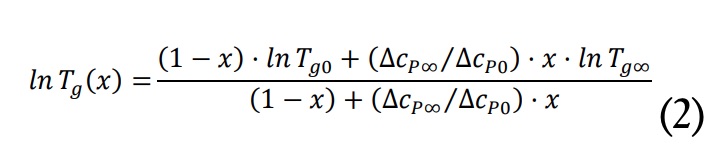 En el caso del material dual EBL70/ S4 se determinaron también las propiedades en el estado intermedio (Tgint y ?c Pint). Se establecieron dos relaciones Tg (x) independientes para la primera y la segunda etapas de curado [3-15-16].
En el caso del material dual EBL70/ S4 se determinaron también las propiedades en el estado intermedio (Tgint y ?c Pint). Se establecieron dos relaciones Tg (x) independientes para la primera y la segunda etapas de curado [3-15-16].
Análisis cinético
Para la modelización cinética se ha utilizado un modelo cinético basado en múltiples elementos autocatalíticos en paralelo [3,17] con un periodo de inducción ficticio para modelar adecuadamente el arranque de la reacción. El curado en el periodo de inducción se ha modelizado de la siguiente manera:
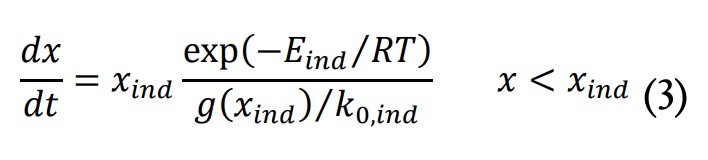 Donde Xind es un grado de conversión correspondiente al periodo de inducción ficticio, con un valor de 0,01. Los parámetros Eind y g(xind )/k0,ind se han determinado para el grado de conversión x=xind=0,01 mediante análisis isoconversional integral no lineal utilizando información isotérmica y dinámica [3,17]. Pasado el periodo de inducción, el curado se ha modelizado mediante las siguientes expresiones:
Donde Xind es un grado de conversión correspondiente al periodo de inducción ficticio, con un valor de 0,01. Los parámetros Eind y g(xind )/k0,ind se han determinado para el grado de conversión x=xind=0,01 mediante análisis isoconversional integral no lineal utilizando información isotérmica y dinámica [3,17]. Pasado el periodo de inducción, el curado se ha modelizado mediante las siguientes expresiones:
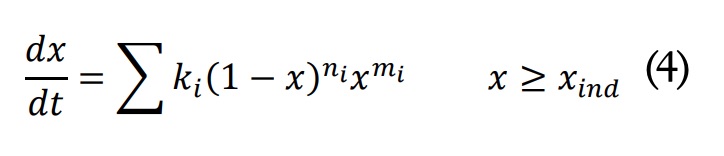 Donde ki es una constante cinética con una dependencia térmica tipo Arrhenius ki=k0,i exp–(-Ei?RT), con energía de activación Ei y factor preexponencial k0,i; ni; y mi son los órdenes aparentes de reacción del elemento autocatalítico. Los parámetros cinéticos se han determinado mediante regresión no lineal múltiple a partir de los datos experimentales de velocidad de reacción determinados experimentalmente mediante DSC.
Donde ki es una constante cinética con una dependencia térmica tipo Arrhenius ki=k0,i exp–(-Ei?RT), con energía de activación Ei y factor preexponencial k0,i; ni; y mi son los órdenes aparentes de reacción del elemento autocatalítico. Los parámetros cinéticos se han determinado mediante regresión no lineal múltiple a partir de los datos experimentales de velocidad de reacción determinados experimentalmente mediante DSC.
Simulación
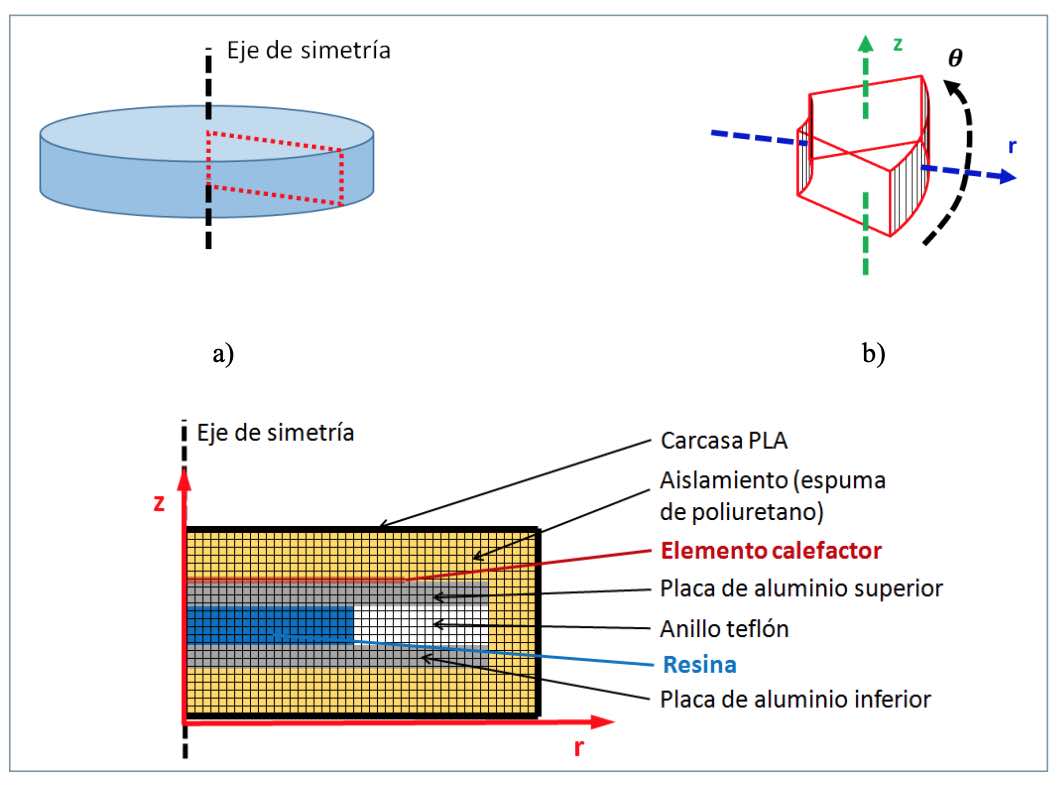
El escenario elegido fue la simulación de piezas compuestas procesadas por moldeo por transferencia de resina, centrándose únicamente en la etapa de curado. Pese a que el molde es un elemento tridimensional, las simulaciones se realizaron asumiendo la transferencia de calor bidimensional con simetría cilíndrica. En la figura 2 se puede observar el esquema de la geometría utilizada para la simulación.
La figura 2.a muestra un esquema simplificado del molde y la sección transversal estudiada, y en la figura 2.b se representa un elemento finito característico, con espesor ?z y ?r en las direcciones axial y radial, respectivamente. En la ampliación de la sección de la figura 2.c se pueden observar distintas zonas correspondientes a los componentes del molde, y una esquematización del mallado. La probeta, ya sea con resina sola o composite (resina + fibra) de espesor L se cura entre las dos partes del molde de aluminio y el anillo de teflón que controla el espesor de la probeta. Todo el conjunto está protegido mediante una capa de espuma aislante y una carcasa de PLA. El mallado se ha realizado con espesores ?z y ?r variables para adaptarse a las dimensiones de los diferentes componentes. Se han considerado las distintas propiedades de los materiales en las distintas zonas para modelizar correctamente la difusión de calor. La ecuación constitutiva para la disipación de calor y la generación de calor es:
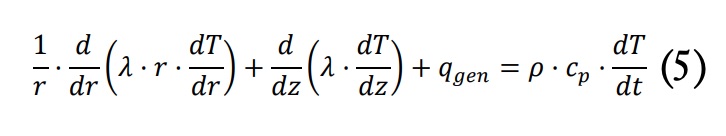 Donde ?, ? y cp son la conductividad térmica efectiva, la densidad y la capacidad calorífica específica, respectivamente, y T es la temperatura. Se ha supuesto insignificante la resistencia a la transferencia de calor entre la resina y las fibras de refuerzo. La dirección transversal está indicada por la letra z y la radial mediante la letra r. Debido a la simetría cilíndrica no aparece el ángulo de revolución e . En la expresión, el término qgen es el calor generado por unidad de volumen y solamente está presente en los elementos donde se encuentra la resina y la resistencia calefactora. En el caso de la generación de calor correspondiente al curado de la resina, se puede expresar como:
Donde ?, ? y cp son la conductividad térmica efectiva, la densidad y la capacidad calorífica específica, respectivamente, y T es la temperatura. Se ha supuesto insignificante la resistencia a la transferencia de calor entre la resina y las fibras de refuerzo. La dirección transversal está indicada por la letra z y la radial mediante la letra r. Debido a la simetría cilíndrica no aparece el ángulo de revolución e . En la expresión, el término qgen es el calor generado por unidad de volumen y solamente está presente en los elementos donde se encuentra la resina y la resistencia calefactora. En el caso de la generación de calor correspondiente al curado de la resina, se puede expresar como:
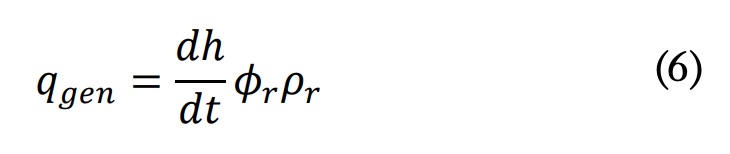 Donde dh/dt es el calor de reacción liberado por unidad de tiempo y unidad de masa de la resina, er es la fracción en volumen de resina y rr es la densidad de la resina. En el caso de un curado en una etapa, el calor liberado se puede expresar como:
Donde dh/dt es el calor de reacción liberado por unidad de tiempo y unidad de masa de la resina, er es la fracción en volumen de resina y rr es la densidad de la resina. En el caso de un curado en una etapa, el calor liberado se puede expresar como:
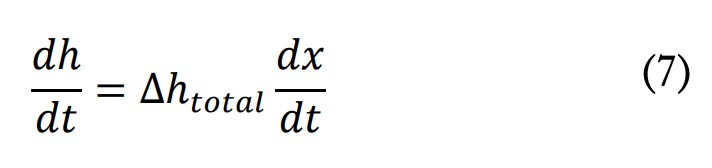 Donde ?htotal es el calor total de la reacción en J/g, x es el grado de conversión del sistema de reacción y dx/dt es la velocidad de reacción. En el caso de un sistema de curado dual, la expresión pasa a ser:
Donde ?htotal es el calor total de la reacción en J/g, x es el grado de conversión del sistema de reacción y dx/dt es la velocidad de reacción. En el caso de un sistema de curado dual, la expresión pasa a ser:
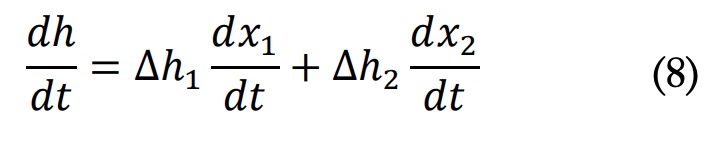 Donde los subíndices 1 y 2 indican el primer y segundo proceso, respectivamente. El sistema dual es similar a otro estudiado anteriormente [3] y puede asumirse un comportamiento estrictamente secuencial, por lo cual el segundo proceso solo se inicia cuando el primero ha finalizado.
Donde los subíndices 1 y 2 indican el primer y segundo proceso, respectivamente. El sistema dual es similar a otro estudiado anteriormente [3] y puede asumirse un comportamiento estrictamente secuencial, por lo cual el segundo proceso solo se inicia cuando el primero ha finalizado.
En el caso de la resistencia calefactora se ha utilizado un valor de qgen con una capacidad máxima de 0,011 W/ mm3 de acuerdo con sus dimensiones y potencia, que solo se activa de acuerdo con el programa térmico establecido. La programación térmica seguida para realizar el proceso de curado dual se estableció en 5 etapas: (1) calentamiento a 1 ºC/min hasta la temperatura de la primera etapa (40-50 ºC), (2) permanencia durante 60 minutos, (3) calentamiento a 1 ºC/min hasta la temperatura de la primera etapa (70-80 ºC), permanencia durante 60 minutos y (5) enfriamiento hasta condiciones ambientales a 1 ºC/min. La activación de la resistencia calefactora tiene lugar siempre que la temperatura en un nodo de control, correspondiente a la sonda superior de temperatura de la placa de aluminio superior, sea inferior a la del programa. De todos los datos de la simulación se extrajeron las temperaturas correspondientes al eje de simetría (r = 0) y en las posiciones correspondientes a la mitad de la placa superior, la mitad de la muestra y la mitad de la placa inferior, equivalentes a la posición de las sondas de temperatura experimentales.
Las propiedades termofísicas efectivas de las resinas compuestas se calcularon utilizando modelos disponibles en la literatura especializada para compuestos reforzados con fibra de vidrio. Todas las propiedades dependen del contenido de fibra, y en este trabajo se ha empleado una fracción de volumen de relleno qr = 0,35-0,40, similar a otros sistemas compuestos reportados en la literatura especializada [6]. Para la conductividad térmica se ha utilizado el siguiente modelo [18]:
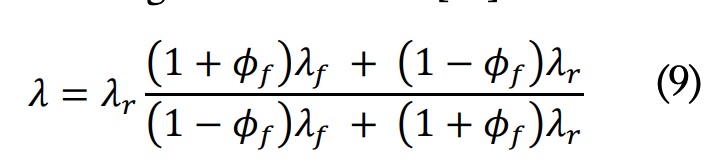 En la expresión anterior, hr y hf son las conductividades térmicas de la resina y la fibra, respectivamente, y qf es la fracción de volumen de fibra. El valor de hr se obtuvo experimentalmente y el valor de hr se supuso de 0,9 Wm?1 K?1. Pese a que es posible que exista anisotropía por una cierta orientación de las fibras de forma perpendicular al eje de simetría del molde, se ha asumido que no había ninguna dirección preferente y por tanto se ha utilizado esta expresión única en todas las direcciones.
En la expresión anterior, hr y hf son las conductividades térmicas de la resina y la fibra, respectivamente, y qf es la fracción de volumen de fibra. El valor de hr se obtuvo experimentalmente y el valor de hr se supuso de 0,9 Wm?1 K?1. Pese a que es posible que exista anisotropía por una cierta orientación de las fibras de forma perpendicular al eje de simetría del molde, se ha asumido que no había ninguna dirección preferente y por tanto se ha utilizado esta expresión única en todas las direcciones.
Para la capacidad calorífica específica efectiva se utilizó un promedio ponderado:
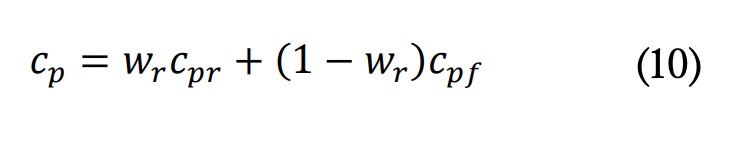 Donde cp y cpf son las capacidades de calor específicas de la resina y la fibra, respectivamente, y wr es la fracción de masa de la resina. El parámetro cpr se calculó a partir de mediciones experimentales y se supuso un valor de 700 Jkg-1K-1. La fracción de masa de la remasa de la resina se calsina se calculó como:
Donde cp y cpf son las capacidades de calor específicas de la resina y la fibra, respectivamente, y wr es la fracción de masa de la resina. El parámetro cpr se calculó a partir de mediciones experimentales y se supuso un valor de 700 Jkg-1K-1. La fracción de masa de la remasa de la resina se calsina se calculó como:
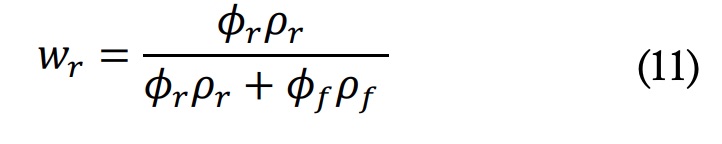 Donde lr y lf son las densidades de la resina y la fibra, respectivamente. El parámetro lr , se calculó experimentalmente y para el valor de lf se asumió un valor de 2.200 kgm-3.
Donde lr y lf son las densidades de la resina y la fibra, respectivamente. El parámetro lr , se calculó experimentalmente y para el valor de lf se asumió un valor de 2.200 kgm-3.
La densidad efectiva del composite se calculó como:
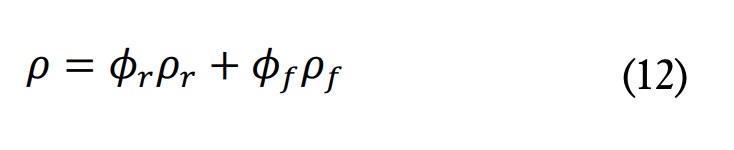 Se establecieron condiciones de contorno en las diferentes fronteras del sistema estudiado. En el eje de simetría, r = 0: se supuso que dT?dr = 0. En la cara exterior, r = rmax, se estableció una condición de frontera
Se establecieron condiciones de contorno en las diferentes fronteras del sistema estudiado. En el eje de simetría, r = 0: se supuso que dT?dr = 0. En la cara exterior, r = rmax, se estableció una condición de frontera
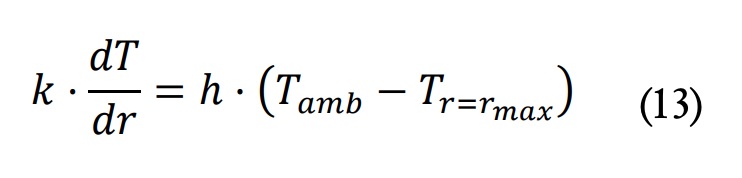 Donde Tamb es la temperatura del aire del entorno, Tr=r_max es la temperatura superficial y h es un coeficiente de convección-radiación que se calculó como:
Donde Tamb es la temperatura del aire del entorno, Tr=r_max es la temperatura superficial y h es un coeficiente de convección-radiación que se calculó como:
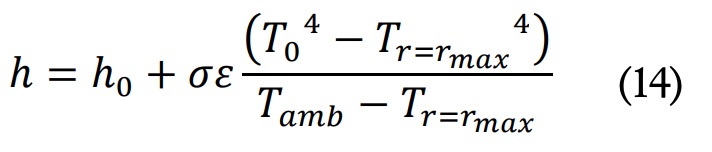 Donde h0 corresponde al coeficiente de convección con el aire del entorno en reposo, m es la constante de Steffan-Boltzmann, ? es la emisividad de la superficie del molde y T0 es la temperatura de la superficie de las paredes de la habitación. Se asumieron valores, h0=5 W/m2 K, m·<W?m2 K4 , ? =0.9 y T0=Tamb. En ausencia de monitorización de la temperatura ambiental, se asumió igual a la temperatura inicial del ensayo.
Donde h0 corresponde al coeficiente de convección con el aire del entorno en reposo, m es la constante de Steffan-Boltzmann, ? es la emisividad de la superficie del molde y T0 es la temperatura de la superficie de las paredes de la habitación. Se asumieron valores, h0=5 W/m2 K, m·<W?m2 K4 , ? =0.9 y T0=Tamb. En ausencia de monitorización de la temperatura ambiental, se asumió igual a la temperatura inicial del ensayo.
Para las superficies con z=zmax y z=0 las condiciones de contorno que se establecieron fueron, respectivamente

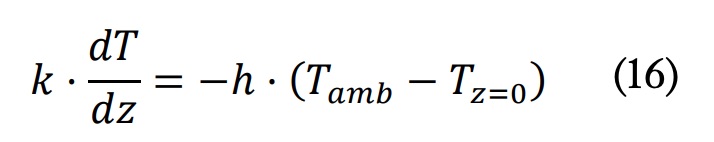 Donde Tz=z_max y Tz=0 son las temperaturas superficiales superior y inferior, respectivamente.
Donde Tz=z_max y Tz=0 son las temperaturas superficiales superior y inferior, respectivamente.
La simulación térmica se realizó en MATLAB mediante un algoritmo propio basado en una resolución implícita de la ecuación de difusión de calor (4) mediante el método de las direcciones alternas de manera similar a otros trabajos [19]. El grado de avance de la reacción se modelizó mediante una integración explícita de la ecuación de velocidad. Para controlar la precisión de la integración numérica se discretizó en intervalos de tiempo con un control del paso de integración de la siguiente manera:
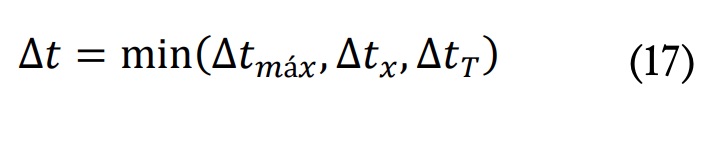 Donde 6tmáx es el máximo paso de integración admitido, 6tx es el máximo tiempo de integración controlado por la reacción y 6tT es el máximo tiempo de integración controlado por gradientes térmicos. Los factores 6tx y 6tT se calcularon antes de ejecutar cada paso de integración como
Donde 6tmáx es el máximo paso de integración admitido, 6tx es el máximo tiempo de integración controlado por la reacción y 6tT es el máximo tiempo de integración controlado por gradientes térmicos. Los factores 6tx y 6tT se calcularon antes de ejecutar cada paso de integración como


Donde ?x máx y ?T máx son un valor máximo permitido de incremento de conversión y temperatura, respectivamente, dx/dt se evalúa a partir de la velocidad de reacción en todos los nodos donde hay resina reactiva, y dT/dt se evalúa utilizando la ecuación (5) de manera explícita en todos los nodos del sistema.
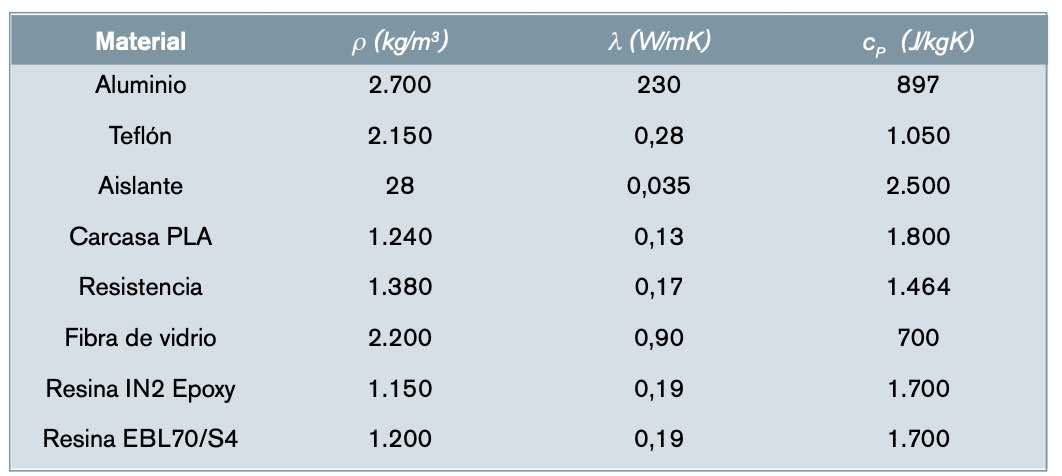
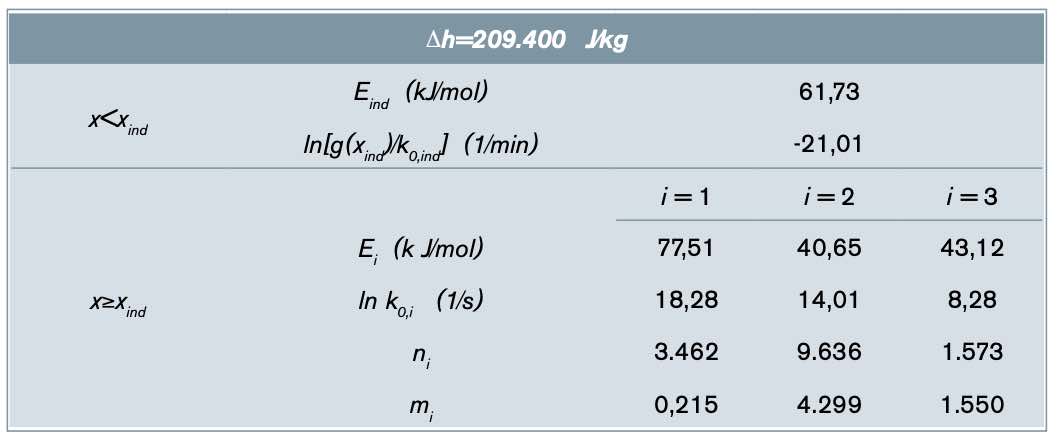
En la tabla 1 se incluyen los datos de propiedades termofísicas utilizadas en el modelo. En el conjunto de materiales se ha supuesto que las propiedades eran independientes de la temperatura. Pese a que las propiedades de las resinas pueden presentar una cierta dependencia térmica y con el grado de avance de la reacción, se han considerado unos valores constantes con validez en el rango de temperaturas experimental. Los valores se obtuvieron a partir de diferentes fuentes como la librería de materiales del software Fusion 360 de Autodesk, la librería de la base de datos de Engineering Equation Solver (EES) y trabajos de otros autores [20,21].
Resultados y discusión
En esta sección se presentan los resultados obtenidos en ambas resinas, con diferentes espesores, con y sin fibras de refuerzo. Para una mayor claridad se ha separado en diferentes apartados.
Resina epoxi IN2
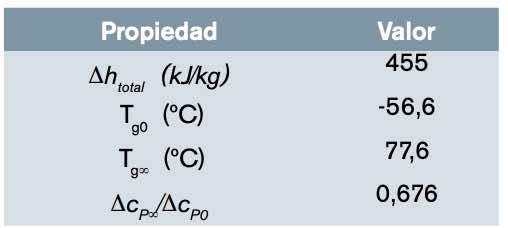
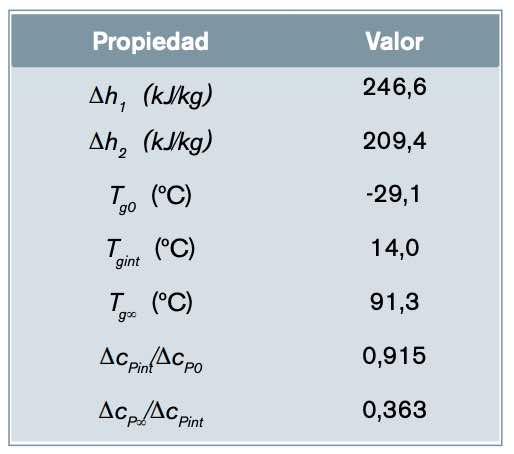
En primer lugar, se realizó una caracterización del curado de la resina IN2 desde un punto de vista calorimétrico. La tabla 2 resume los parámetros principales extraídos del análisis. Cabe destacar la alta exotermicidad del proceso de curado, comparable a otros sistemas epoxi-amina [22,23]. El valor de Tg‘ es moderadamente alto, lo que hace que el material completamente curado presente un comportamiento elástico y rígido a temperatura ambiente o ligeramente superior. El alto valor de 6cP‘?6cP0 es una indicación de que el grado de entrecruzamiento del material es moderado.

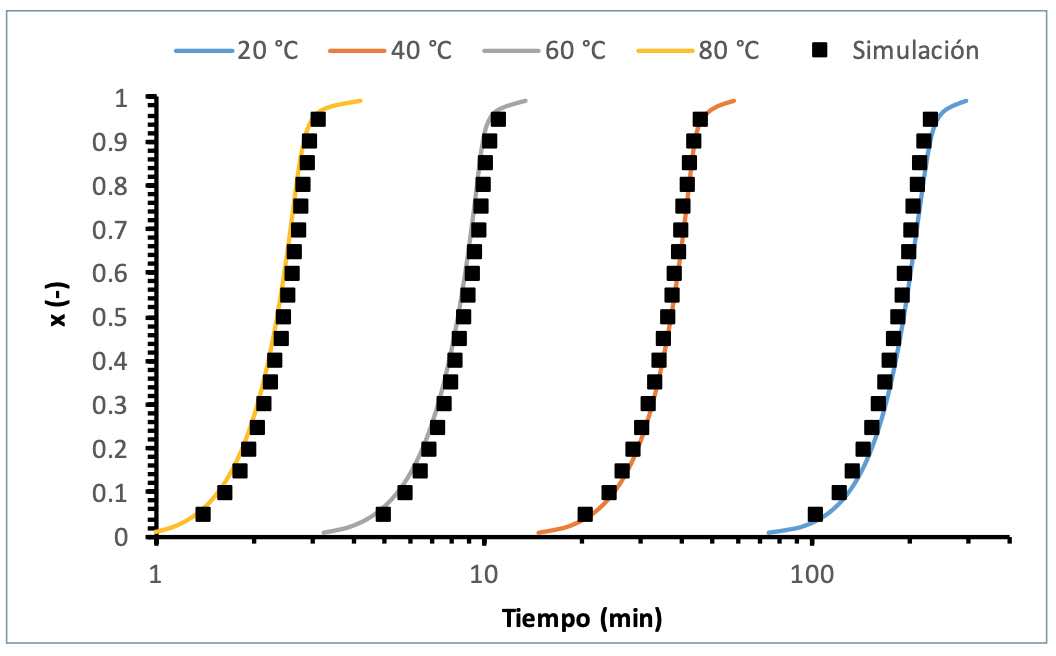
La tabla 3 muestra el calor de reacción y los parámetros cinéticos para la formulación IN2. La figura 3 compara datos experimentales con los resultados de la simulación. El ajuste entre los datos experimentales y la simulación es excelente, como se puede ver en la figura. Pese a que el valor de Tg‘ está por debajo de 80 ºC, no se observó un efecto apreciable de la vitrificación durante el proceso de curado, al contrario de lo que pasa en sistemas con Tg‘ más alta [22]. Por tanto, el modelo cinético utilizado se puede considerar válido para describir el proceso de curado en las condiciones experimentales. El rango de temperaturas experimental de los análisis cinéticos abarca de los 40 a los 250 ºC, por lo que son de una gran fiabilidad de cara a las simulaciones. El proceso de curado es moderadamente lento; necesita cerca de 4 horas para completarse a 80 ºC, por lo que se espera que el control de la exotermicidad durante el procesado sea fácil.
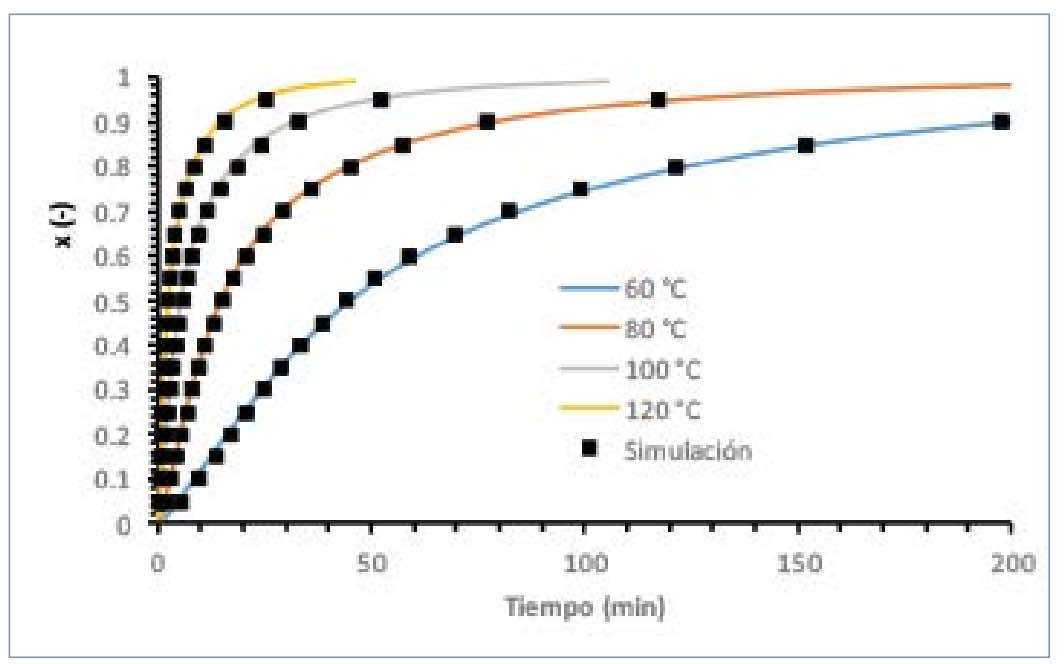
Los valores de las otras propiedades termofísicas se muestran en la tabla 1. El análisis de la cP puso de manifiesto que presentaba muy poca variación en el estado relajado, por encima de su Tg, con valores alrededor de 1.700 J/kgK. Durante las simulaciones se verificó que el material se encontraba a temperaturas superiores a la Tg determinada mediante la relación Tg(x) de Venditti y Gillham y los parámetros de la tabla 2. El valor de la conductividad térmica h se asumió constante e igual a 0,19 W/ mK, similar al obtenido para sistemas similares mostrados en la literatura especializada [3,13]. El hecho de que las propiedades termofísicas que constituyen la difusividad térmica de la resina se consideren constantes durante el curado es una posible fuente de error a tener en cuenta en el análisis de los resultados, habida cuenta de que propiedades como h presentan una dependencia con la temperatura y el grado de conversión [5,24,25].
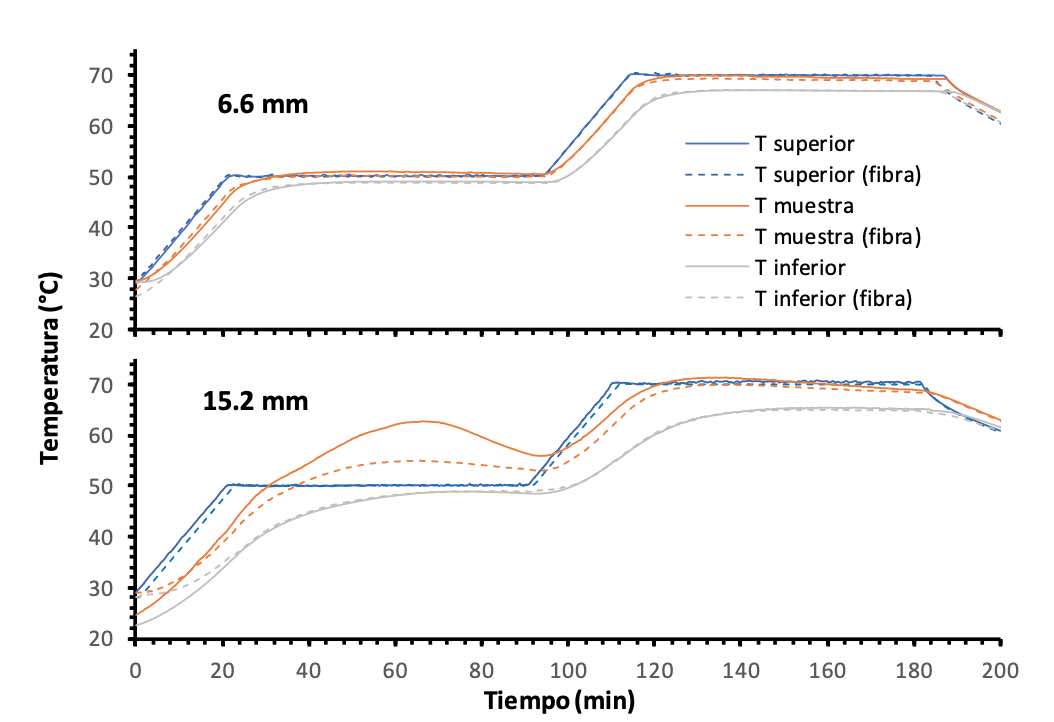
En la figura 4 se comparan los diferentes perfiles de temperatura (placa superior, inferior e interior de muestra) obtenidos de los distintos experimentos realizados con la resina IN2. En el gráfico superior se representan los resultados para el molde de 6,6 mm sin fibra y con fibra con una fracción en volumen del 31,9%, y en el gráfico inferior los obtenidos con el molde de 15,2 mm, siendo la fracción de fibra del 27,8%. Se puede observar la clara inercia térmica que experimenta el molde durante su calentamiento, a partir de la diferencia entre las temperaturas de las placas superior (donde está situada la resistencia calefactora) y la placa inferior. Esta inercia térmica es mayor, lógicamente, en el molde de 15,2 mm. Hay que destacar que en el molde de 6,6 mm se produce un ligero recalentamiento en el interior de la muestra, hasta 1-2 grados por encima de la temperatura de programación de la placa superior en la primera etapa isotérmica, que se atenúa con la presencia de fibra. Sin embargo, en el molde de 15,2 mm, el recalentamiento que experimenta la resina por la acumulación de calor en el interior del molde es mucho más significativo, alcanzando un pico 13 ºC por encima de la temperatura de programación. La temperatura no acaba de descender cuando empieza el segundo calentamiento, donde se observa otro pequeño pico debido a la acumulación de calor. En este caso, el efecto de la fibra (el 27,8% en volumen) sí que es significativo, reduciendo de manera importante el pico de recalentamiento inicial hasta los 5 ºC por encima de la temperatura de programación. La presencia de la fibra contribuye tanto a disminuir la cantidad de calor generada como a facilitar su disipación debido al incremento en conductividad térmica de la muestra. Estos resultados ponen de manifiesto que este dispositivo experimental es sensible a fenómenos térmicos de distinta intensidad.
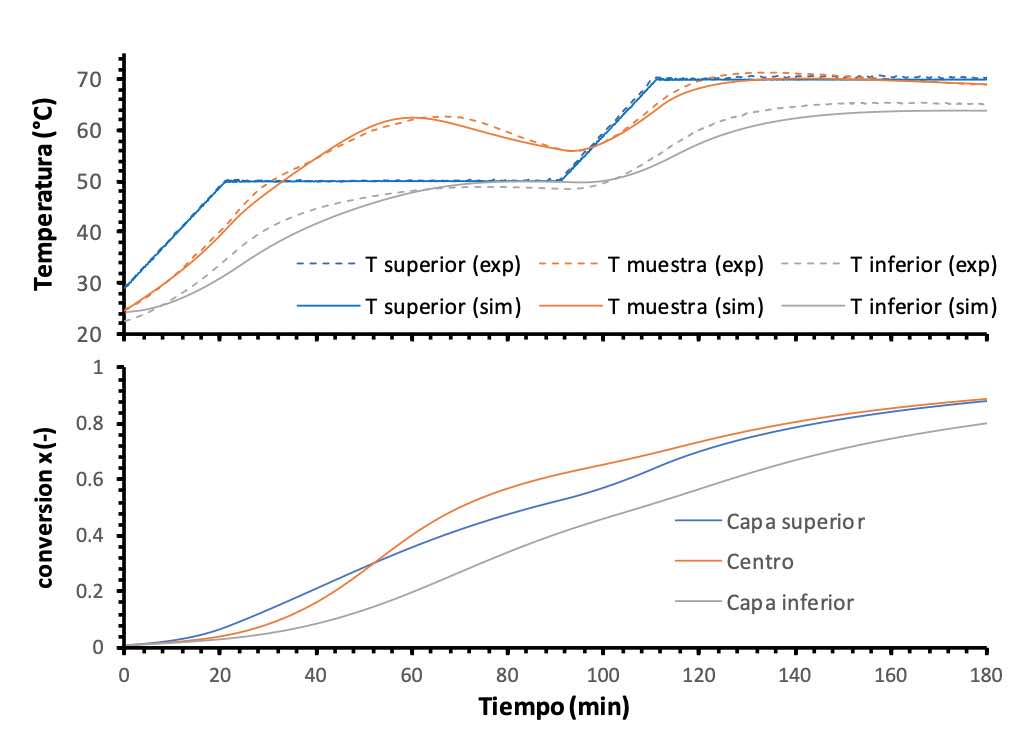
Con el fin de validar el modelo de simulación, se han analizado dos casos extremos. Por un lado, el molde de 6,6 mm con resina IN2 y el 31,9% en volumen de fibra, que presenta una menor acumulación y mejor disipación de calor (Fig. 5) y, por otro, el molde de 15,2 mm sin fibra, con una mayor inercia térmica y acumulación de calor (Fig. 6). Puesto que no se ha analizado experimentalmente, en la programación de la simulación se ha asumido que la temperatura del entorno corresponde con la temperatura inicial del sistema de la placa inferior del molde y se han utilizado los mismos tiempos de calentamiento y residencia a las temperaturas programadas. Se ha tenido en cuenta el tiempo de preparación e infusión de la muestra para establecer la conversión inicial de la resina al inicio de la simulación.
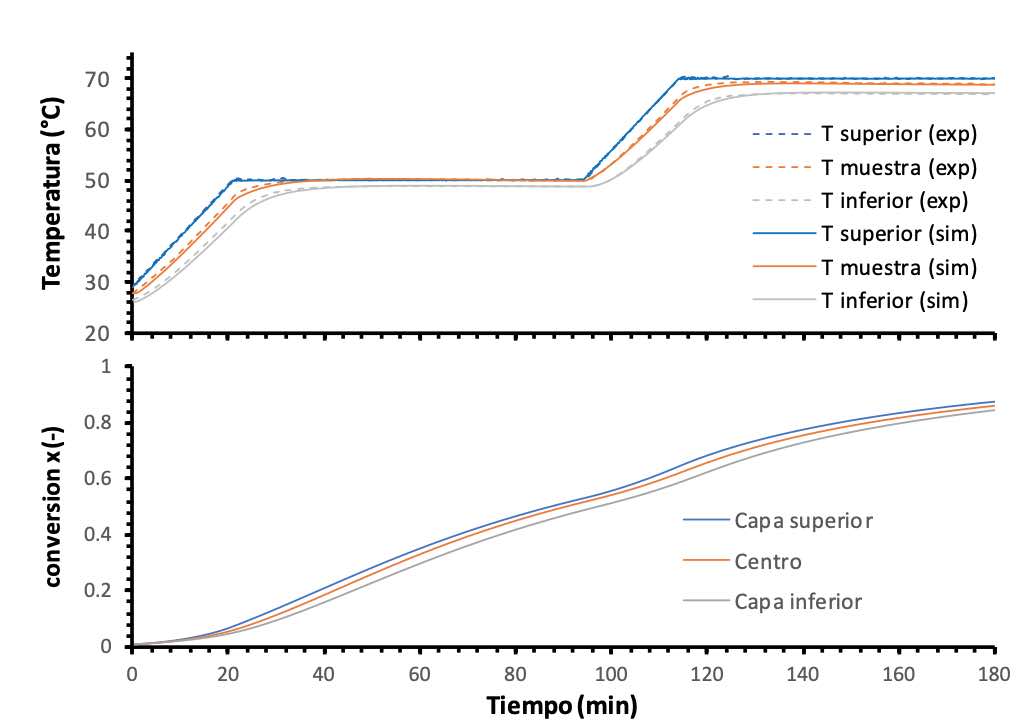
La figura 5 muestra como en el caso del molde de 6,6 mm de grosor los resultados de la simulación son muy cercanos a los resultados experimentales. En el gráfico superior se observa que tanto la inercia térmica como la baja acumulación de calor están correctamente representadas por el modelo. Hay que destacar que los gradientes térmicos son muy reducidos y controlados durante el proceso, lo que hace que la evolución de la conversión durante el proceso sea muy uniforme, como se ve en el gráfico inferior; la conversión es un poco mayor en la capa de material en contacto con la placa superior a lo largo del proceso de curado. En la figura 6
se pueden observar los resultados de la resina epoxi sin fibra con 15,2 mm de espesor. Se puede observar claramente como la simulación permite reproducir de manera bastante fiel la inercia térmica del molde, la acumulación de calor y el moderado disparo térmico que tiene lugar debido a la exotermicidad del curado y la baja capacidad de disipación térmica de la resina y el conjunto del molde. En este caso, cabe esperar un mayor gradiente de conversión a lo largo del proceso de curado y, de hecho, se observa que el grado de conversión es mayor en la zona central de la muestra debido al efecto del disparo térmico en la cinética del curado.
La similitud entre la simulación y los datos experimentales es en ambos casos es destacable. Las discrepancias experimentales son aparentemente mayores en el molde de 15,2 mm, pero el resultado sigue siendo aceptable. En los otros casos (6,6 mm sin fibra, 15,2 mm con fibra) los resultados fueron comparativamente similares. Hay que tener en cuenta, por un lado, la incertidumbre experimental asociada al montaje del molde, la preparación de la muestra y el posicionamiento y calibración de las sondas de temperatura, y el hecho de que no se monitorizara la temperatura del entorno, como posibles fuentes de error. Por otro lado, se han hecho simplificaciones importantes desde un punto de vista geométrico en el modelo de simulación. Hay una cierta imprecisión en algunos valores de propiedades termofísicas y también incertidumbre en las condiciones de contorno, que no fueron determinadas experimentalmente. El modelo empleado para determinar la conductividad térmica en presencia de fibra es mejorable, aunque su posible impacto negativo queda atenuado por la efectiva distribución del calor en las placas de aluminio superior e inferior. Por otro lado, hay que destacar que en todos los casos se verificó que, efectivamente, la temperatura durante el proceso de curado era claramente superior a la Tg(x) determinada mediante la expresión (2), lo que refuerza la validez general del modelo simplificado de propiedades termofísicas de la resina empleado en la simulación.
Hay que destacar que, en ningún caso, estos perfiles de conversión y temperatura están optimizados desde un punto de vista de control térmico o mecánico [1,5,18], debido a la limitación experimental del molde en la velocidad de calentamiento y enfriamiento. Además, la resina epoxi IN2 es una resina comercial de amplia utilización y, por tanto, con un comportamiento largamente conocido. Sin embargo, los experimentos realizados con la resina epoxi IN2 tenían como principal objetivo la verificación de la utilidad del molde para analizar el procesado de materiales compuestos y la validación del comportamiento térmico del molde determinado mediante el modelo de simulación, además de disponer de un valor base para la comparación posterior con la resina dual EBL70/S4, un sistema dual similar al descrito en la literatura especializada [3-26] con el que se pretende probar experimentalmente el concepto y la aplicación de la liberación controlada de calor (sequential heat release, SHR) en el procesado de materiales compuestos, hasta ahora descrito como una mera posibilidad desde un punto de vista teórico [3].

En la figura 7 se muestran diferentes imágenes de las probetas obtenidas con la resina IN2. En la figura 7a se muestra la probeta sin fibra justo después de desmoldar y aún dentro del anillo de teflón. Se puede apreciar con claridad que la resina es transparente y el sensor de temperatura colocado en el centro de la probeta. En la figura 7b se aprecia el momento de desmoldeo de una probeta de 15,2 mm con resina de refuerzo. Se puede apreciar que la distribución de la fibr.a es uniforme en el espesor. En la figura 7c se aprecia la misma probeta que la figura 7b, pero fuera del molde y en vista lateral, donde se aprecia que el sensor de temperatura está en la mitad del espesor.
Resina EBL70/S4
La formulación EBL70/S4 es un sistema dual basado en la reacción tiolepoxi con exceso de epoxi. Este tipo de sistema dual ha sido descrito anteriormente [4], y las reacciones tiolepoxi y homopolimerización aniónica de grupos epoxi han sido descritas con detalle recientemente [27,28]. El carácter secuencial de este sistema dual se fundamente en la gran diferencia desde el punto de vista cinético entre el primer y el segundo proceso, y la selectividad casi exclusiva del primer proceso en presencia de grupos tiol [27].
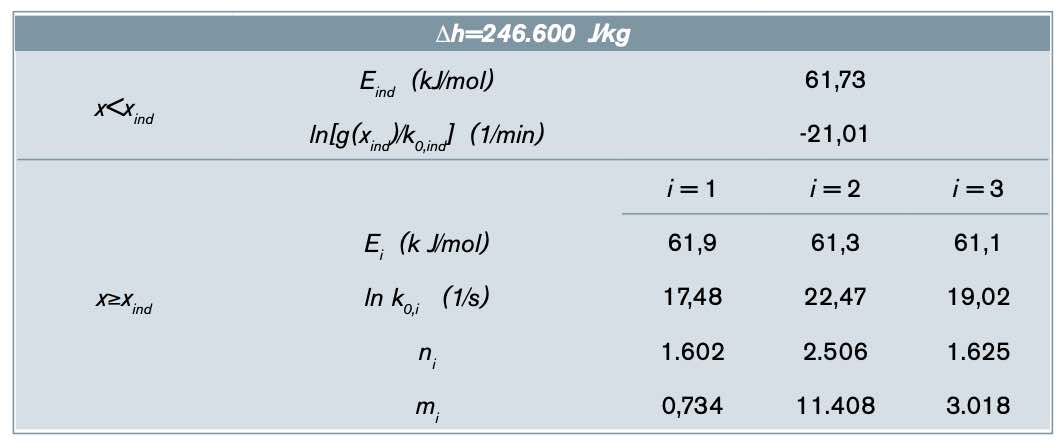
La tabla 4 resume los parámetros principales extraídos del análisis de la primera y segunda etapa del proceso de curado del sistema EBL70/ S4. Como se puede ver, el calor total de reacción es comparable al de la formulación IN2, pero se encuentra repartido en dos etapas de curado, de la misma manera que para otros sistemas tiol-epoxi similares [3,26,29]. Teniendo en cuenta que la relación tiol-epoxi de este sistema es de r = 0,45, el calor de la primera etapa de reacción concuerda con el valor de 125-130 kJ/eq determinado para la reacción tiol-epoxi [3,26,30], y el calor de la segunda etapa concuerda con un valor de 90-100 kJ/eq para la reacción la simulación con los parámetros de la tabla 5 a los datos cinéticos experimentales del primer proceso. También cabe destacar el comportamiento cinético del primer proceso, con un inicio muy lento, pero un comportamiento fuertemente autocatalítico que hace que el proceso sea completo en muy poco tiempo. A modo de comparación, este primer proceso tarda menos de 4 minutos en completarse a 80 ºC, mientras que el curado de la resina IN2 necesita más de 3 horas a la misma temperatura. Este comportamiento hace que exista el riesgo de un disparo térmico importante [3], lo que podría llegar a activar el segundo proceso de curado si las condiciones de procesado no son adecuadas, invalidando, en consecuencia, el control secuencial del proceso.
Se hicieron simulaciones preliminares del proceso de curado en el molde de 6,6 mm con el fin de establecer condiciones seguras de procesado para garantizar que no se produjera un excesivo disparo térmico durante la primera reacción de curado, y se estableció un programa de curado en dos etapas, a 40 y 80 ºC, con una velocidad de calentamiento de 1 ºC/min. Se realizó el experimento y se rehizo la simulación teniendo en cuenta el tiempo de preparación e infusión de la muestra. Los resultados se muestran en las figuras 9 y 10.
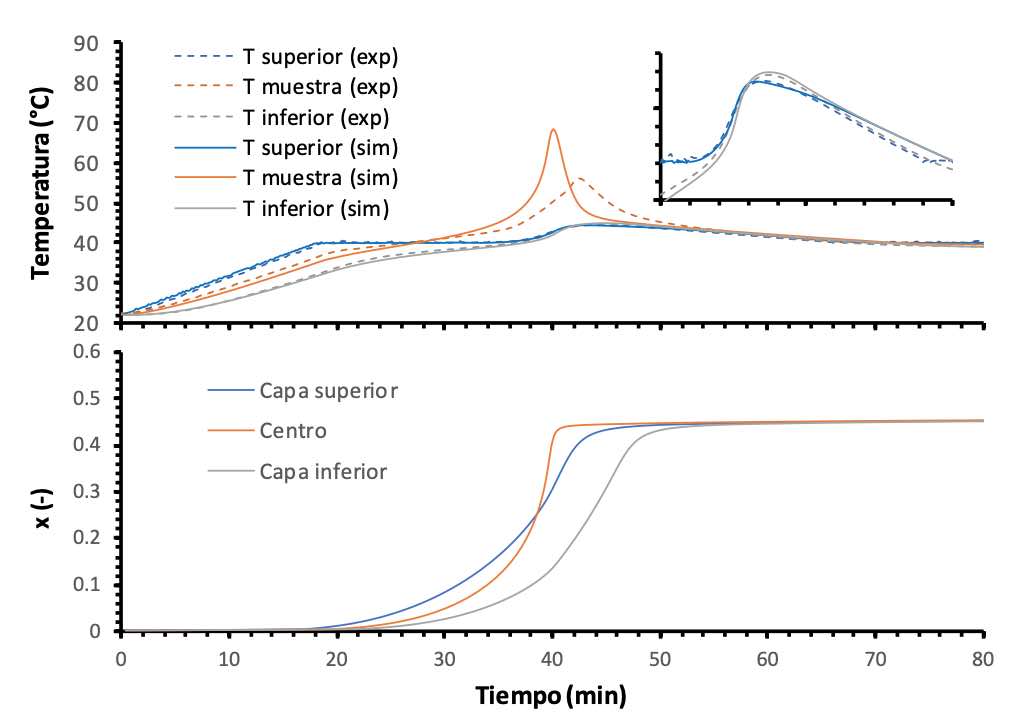
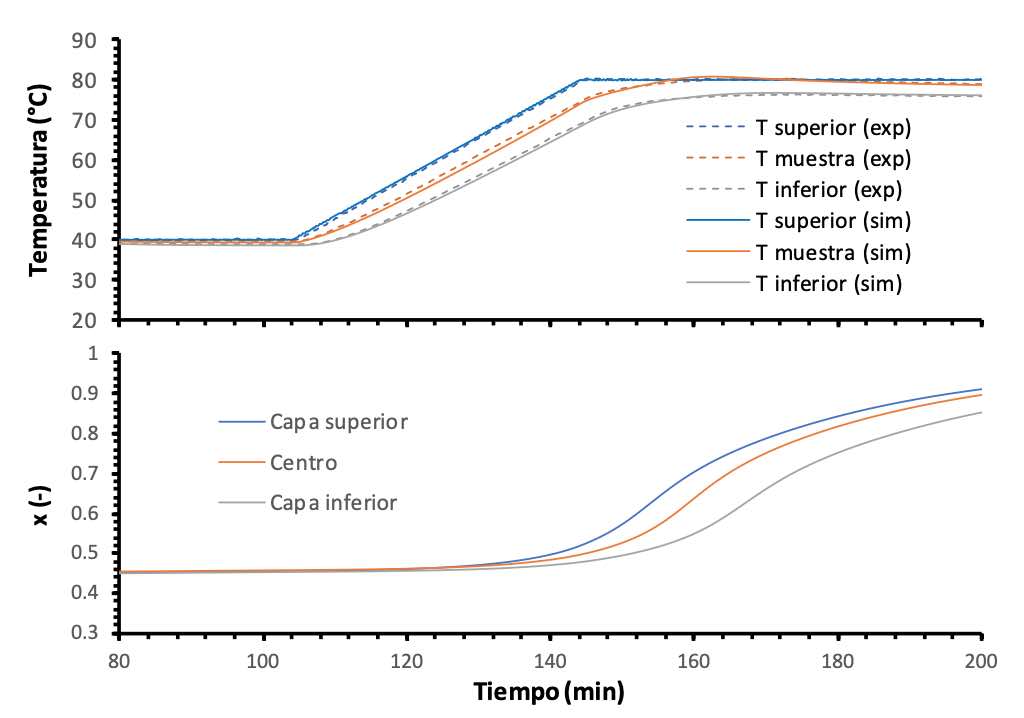
La figura 9 muestra la primera parte del proceso de curado a 40 ºC, en el que se puede ver como tiene lugar un brusco, pero controlado disparo térmico correspondiente al calor liberado por la primera reacción que tiene lugar en la formulación EBL70/S4, la reacción tiol-epoxi. Como se puede ver, hay una diferencia entre el disparo térmico registrado en el interior de la muestra y el determinado mediante la simulación. Sin embargo, se repitió el experimento, pero únicamente la primera parte, y se obtuvo un resultado muy similar a la simulación, por lo que el resultado mostrado en la figura pudo ser debido a algún error de medida o posicionamiento de la sonda empleada. Donde sí se aprecia una buena correspondencia entre la simulación y el experimento es en la lectura de las sondas de las placas superior e inferior (véase inserción en el gráfico superior), que experimentan un calentamiento de unos 5 ºC por encima de la temperatura de programa debido al calor liberado de manera tan brusca por la primera reacción. La coincidencia entre el perfil de temperatura simulado y el experimental confirma que la reacción tuvo lugar de la manera determinada por la simulación. El gráfico inferior muestra la evolución del grado de conversión en las capas en contacto con las placas superior e inferior, y en el centro de la muestra. La autoaceleración observada en la zona central es consecuencia del disparo térmico en el interior debido a la acumulación de calor. Gracias a que la temperatura alcanzada no es excesiva, el segundo proceso reactivo no llega a activarse y la conversión alcanzada es uniforme en todo el componente y no supera en ningún caso la conversión de 0,45 correspondiente al final de la primera reacción, con una alta estabilidad antes del inicio del segundo calentamiento. Este es un beneficio importante de la resina dual en comparación con la resina convencional, ya que el control cinético de los procesos reactivos atenúa el efecto de posibles disparos térmicos, permitiendo obtener propiedades intermedias controladas y uniformes y facilitando el posterior control de la reacción [18], aunque en este caso el dispositivo experimental presente limitaciones importantes en cuanto a velocidad de calentamiento. La Figura 10 muestra la continuación del proceso de curado, el segundo calentamiento y la residencia a 80 ºC. Se puede observar como se activa la segunda reacción, la homopolimerización del exceso de grupos epoxi sin reaccionar, llegándose a producir un pequeño disparo térmico después de la rampa de calentamiento debido al calor liberado pero de mucha menor intensidad debido a que el segundo proceso es mucho más lento en comparación [3-4]. Se observa también como la simulación predice correctamente el comportamiento experimental, de manera similar a todos los casos anteriores.
Estos resultados son de gran valor ya que prueban que es posible predecir de manera fiable el procesado por etapas de un sistema de curado dual secuencial, y por tanto controlar el grado de avance de la reacción y su comportamiento térmico bajo condiciones seguras establecidas a priori mediante simulación. Estos resultados complementan por tanto el trabajo teórico publicado anteriormente [3] y confirman la validez del concepto de liberación de calor secuencial (sequential heat release, SHR) con aplicación en el procesado de materiales compuestos. Además, se ha probado que el dispositivo experimental es suficientemente sensible para detectar sucesos exotérmicos tanto en el interior de la muestra como en las placas en contacto, lo que puede ser aprovechado para diseñar procesos de curado por etapas con un control más fiable, teniendo en cuenta que la incertidumbre experimental asociada a la preparación de la muestra puede producir variaciones en la respuesta que pueden ser monitorizadas en línea y pueden utilizarse para reajustar los parámetros de procesado a medida que tiene lugar.
Conclusiones
En este trabajo se ha presentado la validación experimental de un dispositivo instrumentado para la monitorización de procesos de curado por etapas. Se han analizado dos resinas termoestables, una resina epoxi-amina bicomponente convencional y un sistema de curado dual secuencial basado en química tiol-epoxi. Se ha estudiado el efecto del grosor de muestra y la presencia de refuerzo de fibra de vidrio. Los resultados experimentales han sido comparados con los obtenidos mediante simulación de un modelo simplificado del molde basado en coordenadas cilíndricas, empleando propiedades termofísicas constantes características de cada componente del molde e información termocinética detallada del proceso de curado.
Se ha podido comprobar que el presente dispositivo experimental es sensible a sucesos térmicos de distinta intensidad y duración, lo que permite obtener respuestas diferenciadas en función del grosor de la muestra, la exotermicidad y la cinética de la reacción, y la presencia de cargas que faciliten la disipación del calor generado. Para ello, se puede utilizar no solamente datos obtenidos en sondas de temperatura ubicadas en el interior de la muestra, sino también en las placas del molde, lo que permite una sencilla monitorización y control en línea del proceso de curado.
Se ha definido un modelo de simulación basado en una geometría simplificada del molde que ha permitido reproducir de manera fiable los procesos de curado bajo distintas condiciones. A pesar de algunas de las simplificaciones inherentes en el modelo utilizado y en las propiedades termofísicas de la resina y el material compuesto, el modelo de simulación permite el establecimiento, a priori, de condiciones seguras de procesado u optimizadas para obtener perfiles de curado controlados.
El análisis de la resina de curado dual secuencial ha permitido validar experimentalmente el concepto de liberación secuencial de calor (SHR) como posible metodología para la mejora del procesado de materiales compuestos. Se ha comprobado que es posible establecer condiciones seguras para la obtención de materiales intermedios estables y con propiedades uniformes, gracias al control cinético de la secuencia de curado. Se espera poder evaluar próximamente el efecto de distintos tipos de refuerzo, el grosor de la muestra y el efecto del calentamiento por las placas superior e inferior del molde en estos sistemas, con el fin de aproximarse a condiciones de procesado más realistas y analizar en un futuro las propiedades de materiales compuestos basados en sistemas de curado dual.
Agradecimientos
Los autores agradecen al Ministerio de Ciencia, Innovación y Universidades, al Fondo Europeo de Desarrollo Regional (Feder) (MAT2017-82849- C2-1-R y MAT2017-82849-C2-2-R) y a la Generalitat de Catalunya (2017- SGR-77 y el programa Serra Húnter) el apoyo económico.
Referencias
[1] Ruiz E., Trochu F., “Multi-criteria thermal optimization in liquid composite molding to reduce processing stresses and cycle time”, Composites Part A: Applied Science and Manufacturing 37, 913-24 (2006).
[2] Nair D.P., Cramer N.B., McBride M.K., Gaipa J.C., Shandas R., Bowman C.N., “Enhanced two-stage reactive polymer network forming systems”, Polymer 53, 2429-34 (2012).
[3] Romero M., Fernández-Francos X., Ramis X., “Sequential heat release: an innovative approach for the control of curing profiles during composite processing based on dualcuring systems”, Polymer International 68, 527–45 (2019).
[4] Fernández-Francos X., Konuray A.-O., Belmonte A., De la Flor S., Serra À., Ramis X., “Sequential curing of off-stoichiometric thiol-epoxy thermosets with custom-tailored structure”, Polymer Chemistry 7, 2280-90 (2016).
[5] Struzziero G., Skordos A.A., “Multi-objective optimisation of the cure of thick components”, Composites Part A: Applied Science and Manufacturing 93, 126-36 (2017).
[6] Ruiz E., Trochu F., “Numerical analysis of cure temperature and internal stresses in thin and thick RTM parts”, Composites Part A: Applied Science and Manufacturing 36, 806-26 (2005).
[7] Ramis X., Fernández-Francos X., De la Flor S., Ferrando F., Serra A., Click-based dual-curing thermosets and their applications. (2018).
[8] Studer J., Dransfeld C., Masania K., “An analytical model for B-stage joining and cocuring of carbon fibre epoxy composites”, Composites Part A: Applied Science and Manufacturing 87, 282-9 (2016).
[9] Fabregat-Sanjuan A., Fernández-Francos X., Ferrando F., Diseño e instrumentación de un molde para el análisis del curado dual en resinas epoxi. publicaciones@uis.edu.co, Bucaramanga, Colombia, (2019).
[10] Easy Composites, “https://www. easycomposites.co.uk”.: <https://www. easycomposites.co.uk/#!/resin-gel-siliconeadhesive/epoxy-resin/epoxy-infusion-resin. html>.
[11] Feroca, “https://www.feroca.com/es/”.: <https://www.feroca.com/es/fibras-de-vidrioy-tejidos-de-refuerzo/179-fibra-de-vidrio-matde-refuerzo-600-grm.html>.
[12] Recommended reference materials for the realization of physicochemical properties. Blackwell Scientific Publications, (1985).
[13] Hutchinson J.M., Román F., Cortés P., Calventus Y., “Epoxy composites filled with boron nitride and aluminum nitride for improved thermal conductivity”, 4-8 (2017).
[14] Venditti R.A., Gillham J.K., “Relationship between the glass transition temperature (Tg) and fractional conversion for thermosetting systems”, Journal of Applied Polymer Science 64, 3-14 (1997).
[15] Konuray O., Salla J.M., Morancho J.M., Fernández-Francos X., García-Alvarez M., Ramis X., “Time-temperature-transformation (TTT) diagram of dual-curable epoxy thermosets obtained via two sequential epoxyamine condensations”, Thermochimica Acta 678, 178305 (2019).
[16] Areny N., Konuray O., Fernández-Francos X., Salla J.M., Morancho J.M., Ramis X., “Timetemperature-transformation (TTT) diagram of a dual-curable off-stoichiometric epoxy-amine system with latent reactivity”, Thermochimica Acta 666, 124-34 (2018).
[17] Santín D., Konuray O., Fernández-Francos X., Ramis X., “Kinetics analysis and simulation of sequential epoxy dual-curing systems with independent thermal activation”, Thermochimica Acta 673, 158-68 (2019).
[18] Bailleul J.L., Sobotka V., Delaunay D., Jarny Y., “Inverse algorithm for optimal processing of composite materials”, Composites Part A: Applied Science and Manufacturing 34, 695- 708 (2003).
[19] Frulloni E., Salinas M.M., Torre L., Mariani A., Kenny J.M., “Numerical modeling and experimental study of the frontal polymerization of the diglycidyl ether of bisphenol A/ diethylenetriamine epoxy system”, Journal of Applied Polymer Science 96, 1756-66 (2005).
[20] Wu J.-W., Sung W.-F., Chu H.-S., “Thermal conductivity of polyurethane foams”, International Journal of Heat and Mass Transfer 42, 2211-7 (1999).
[21] Alvarez-Lainez M., Rodriguez-Perez M.A., Saja J.A., “Thermal Conductivity of Open-Cell Polyolefin Foams”, Journal of Polymer Science: Part B: Polymer Physics 46, 212-21 (2008).
[22] Santiago D., Fernández-Francos X., Ramis X., Salla J.M., Sangermano M., “Comparative curing kinetics and thermal-mechanical properties of DGEBA thermosets cured with a hyperbranched poly(ethyleneimine) and an aliphatic triamine”, Thermochimica Acta 526, 9-21 (2011).
[23] Konuray A.O., Areny N., Morancho J.M., Fernández-Francos X., Serra À., Ramis X., “Preparation and characterization of dualcurable off-stoichiometric amine-epoxy thermosets with latent reactivity”, Polymer 146, 42-52 (2018).
[24] Sorrentino L., Tersigni L., “A Method for Cure Process Design of Thick Composite Components Manufactured by Closed Die Technology”, Applied Composite Materials 19, 31-45 (2012).
[25] Nawab Y., Tardif X., Boyard N., Sobotka V., Casari P., Jacquemin F., “Determination and modelling of the cure shrinkage of epoxy vinylester resin and associated composites by considering thermal gradients”, Composites Science and Technology 73, 81–7 (2012).
[26] Konuray A., Fernández-Francos X., Ramis X., Serra À., De la Flor S., Belmonte A., “Sequential curing of off-stoichiometric thiol–epoxy thermosets with a custom-tailored structure”, Polymer Chemistry 7, 2280-90 (2016).
[27] Konuray A.O., Fernández-Francos X., Ramis X., “Analysis of the reaction mechanism of the thiol-epoxy addition initiated by nucleophilic tertiary amines”, Polymer Chemistry 8, 5934- 47 (2017).
[28] Fernández-Francos X., “Theoretical modeling of the effect of proton donors and regeneration reactions in the network build-up of epoxy thermosets using tertiary amines as initiators”, European Polymer Journal 55, 35-47 (2014).
[29] Belmonte A., Fernández-Francos X., Serra À., De la Flor S., “Phenomenological characterization of sequential dual-curing of off-stoichiometric thiol-epoxy systems: Towards applicability”, Materials & Design 113, 116-27 (2017).
[30] Guzmán D., Ramis X., Fernández-Francos X., Serra À., “New Catalysts For Diglycidyl Ether Of Bisphenol A Curing Based On Thiol-Epoxy Click Reaction”, European Polymer Journal 59, 377-86 (2014).
[31] Ooi S.K., Cook W.D., Simon G.P., Such C.H., “DSC studies of the curing mechanisms and kinetics of DGEBA using imidazole curing agents”, Polymer 41, 3639-49 (2000)

