Predimensionamiento de turbinas Kaplan y Pelton
Pre-dimensioning Kaplan and Pelton turbines
RESUMEN
Cuando un diseñador se enfrenta al problema de dimensionar
una turbina ya sabe, aproximadamente, en función
del salto y del caudal de equipamiento, el tipo de turbina
que necesita. Sin embargo, no conoce las dimensiones de
la misma. En este artículo se presenta cómo se calcula su
predimensionamiento.
Recibido: 19 de octubre de 2015
Aceptado: 25 de noviembre de 2015
Palabras clave
Turbinas hidroeléctricas, cálculos, caudal, energía eléctrica, centrales hidroelécticas.
ABSTRACT
When a designer faces the problem of sizing a turbine they
already know, approximately, the type of turbine they need
depending on the jump and the flow of equipment. However,
they do not know the dimensions. This article shows how to
calculate pre-dimensioning.
Received: October 19, 2015
Accepted: November 25, 2015
Keywords
Hydroelectric turbines, calculations, flow, electric power, power stations
El término turbina, como tal, fue utilizado por primera vez por un ingeniero militar francés, Claude Burdin, en un análisis teórico sobre las ruedas hidráulicas que ponía el acento en la velocidad de rotación. Un alumno suyo de la Escuela de Minería de Saint Étienne, Benoit Founeyron, en 1834 diseñó y construyó ruedas hidráulicas que alcanzaban, inicialmente, velocidades de rotación de 60 revoluciones por segundo y que proporcionaban hasta 50 caballos.
Posteriormente, fueron evolucionando y en Estados Unidos se empezaron a construir, poco después, turbinas mucho más sencillas. El americano Francis construyó en 1849 una turbina centrípeta de buen rendimiento. Sus buenas condiciones de funcionamiento hicieron que su utilización se generalizara para la obtención de fuerza motriz. Era una versión mejorada y con distribuidor de las citadas en el párrafo anterior. En 1880, el también americano Lester Pelton inventó su máquina hidráulica basada en una rueda de cucharas, que también fue muy utilizada debido a su buen rendimiento y su capacidad de regulación a cargas parciales.
En 1890 se utilizó por primera vez una turbina para la producción de energía eléctrica. A partir de entonces, se desarrollaron diversos tipos de turbinas de forma muy rápida y se mejoraron los diseños existentes.
Se tomó como fundamento la hélice, que inventó el sueco John Ericson en 1836 inicialmente para aplicarla en la propulsión de buques y una vez que se generalizó la utilización de las turbinas, para la generación de energía eléctrica. Se utilizaron las hélices de paso fijo en la construcción de turbinas para aprovechar saltos bajos, que presentaban muchas limitaciones. En 1915 el austriaco Victor Kaplan desarrolló, a partir de las turbinas hélice, una regulación de las palas del rodete que significó una revolución para la explotación de los saltos de poca altura.
Estos tres tipos fundamentales de turbinas, con ligeras modificaciones y modestos aumentos de rendimiento respecto a los originales de finales del s. XIX o primeros de s. XX, cubren, casi por completo, el abanico de saltos hidráulicos que se presentan en la naturaleza. Sin embargo, para los saltos de muy baja altura, era necesario otro tipo de máquina. Se probaron las turbinas Francis en cámara abierta, las mismas con doble tubo de aspiración, las turbinas hélice y las Kaplan.
Apliquemos lo comentado al cálculo de una turbina Kaplan. El primer problema que se encuentra el diseñador a la hora de dimensionar una turbina es que en función del salto y el caudal, ya sabe, más o menos, el tipo de turbina que necesita. Sin embargo no conoce las dimensiones de la misma.
El parámetro más común que se suele utilizar como base es el número específico de revoluciones Ns que se obtiene aplicando la fórmula (1).
Donde:
Ns = número específico de revoluciones (adimensional).
N = revoluciones de la turbina (rpm).
P = potencia de la turbina (P=g*Q*H*ν) (kw).
H = altura del salto (m).
Q = caudal (m3/s).
H= rendimiento (adimensional).
Como en dicha fórmula (1) hay dos incógnitas, Ns y N, para efectuar una aproximación, existen tablas en las que
se especifica el tipo de turbina más
adecuado, en función del Ns. Varían ligeramente
de un autor y/o fabricante a
otro, pero poco (tabla 1).
Sin embargo, en este caso, vamos
a basarnos en una aproximación al
número específico de revoluciones en
el que no intervenga la potencia de
la turbina, que es el expresado en las
ecuaciones (2) y (3).
Sustituyendo en la fórmula (1) tenemos
el Ns de la turbina. Sin embargo,
el valor de n que obtengamos estará
fuera de los escalones normalizados
que se indican en las tablas 2 y 3, de
forma que la turbina gire a una velocidad
tal que el generador pueda interconectarse
a la red eléctrica. Otra
posibilidad es utilizar un grupo multiplicador
de velocidad. Sin embargo,
es una posibilidad que se relega a los
casos en que el generador sea de tales
dimensiones y coste que se haga inviable
económicamente, puesto que
dicha multiplicadora, no deja de ser
otra pérdida de rendimiento adicional.
Solamente se considera cuando el coste
del grupo turbina-alternador supera
el coste del sistema turbina-multiplicadora-
alternador. El Ns definitivo no
será el inicialmente previsto, sino un
valor cercano que permita conjugar
todos los valores comentados.
Una vez fijados Ns y N, se calculan
los demás parámetros de la turbina de
la manera que se indica a continuación.
Para ello, se parte de la expresión
que relaciona el coeficiente de velocidad
periférica ku del rodete con el Ns (4).
El siguiente paso consiste en calcular
el diámetro exterior del rodete
DM, pues es la medida fundamental
que servirá para dimensionar el resto
de los elementos de la turbina que se
indexarán a dicho valor.
Dicho valor también se puede tantear
de forma aproximada aplicando (6).
A continuación se dan una serie de
relaciones entre diversos parámetros
de la turbina y el diámetro exterior
del rodete. Una vez determinado DM
se procede a calcular el resto de las dimensiones
de la turbina de la siguiente
forma:
En la figura 1 se pueden ver las dimensiones
calculadas en las fórmulas
precedentes.
Cálculo de una turbina Kaplan
Para ilustrar un poco mejor el tema, se
incluye a continuación un ejemplo resuelto.
Los valores elegidos se resaltan
en amarillo.
Sustituyendo en la fórmula siguiente:
< Hay que tener en cuenta que el dimensionado del tubo de aspiración en una turbina Kaplan es una labor delicada, pues se recupera una parte muy importante del salto en él. Se deberá de evitar, en lo posible, dimensionar las turbinas Kaplan con una velocidad de rotación N superior a lo que les corresponde. Ello obliga a disminuir la altura de aspiración o incluso a calar el plano del rodete por debajo del nivel del socaz, lo que encarece enormemente la obra civil, aunque disminuye ligeramente el tamaño y el precio de la turbina. No obstante, dicha turbina siempre funcionará forzada, dentro de unos parámetros de funcionamiento que no están dentro de su ámbito de actuación idóneo y tendrá una tendencia a la cavitación mucho mayor. El precio de la obra civil será mayor y no compensará la disminución de precio obtenida en la turbina.
Cálculo de una turbina Pelton
Apliquemos ahora lo comentado al
cálculo de una turbina Pelton. En este
caso, se aplica la misma fórmula (1) y
la tabla 1, al igual que en las turbinas
Kaplan. Sin embargo, al tratarse de
una turbina de acción, se utilizan uno
o varios chorros que inciden sobre la
rueda de cucharas y de los que se desconoce
su número y características.
El diámetro del chorro se tantea
mediante la ecuación (42).
Donde:
d= diámetro del chorro en m.
Por fin Ns se obtiene de forma aproximada de la expresión (43).
Y de la igualdad (44) se obtiene una
aproximación del diámetro exterior de
la rueda Pelton.
Sin embargo, no se ha determinado
todavía el número de chorros. Para
ello hay que calcular el número específico
de revoluciones en función del
número de chorros Nsj o velocidad específica
resultante (45).
El diámetro medio del rodete D3 es
igual al resultado de la ecuación (46);
este valor tiene importancia porque en
función de él se hallarán otros parámetros
de la turbina.
Con este valor se puede tantear de
nuevo el diámetro del chorro aplicando
(47), lo que servirá de comprobación de
seguridad del cálculo realizado en (42).
El diámetro del chorro variará en
función de la velocidad de giro de la
turbina y el número de chorros j se
puede tantear aplicando (48).
En la primera aproximación, en
función del diámetro del chorro, se
obtiene el diámetro de la rueda. En
algunos saltos, se obtienen, en este
primer ensayo, diámetros de la rueda
de cucharas imposibles, por demasiado
pequeños. Por ello, hay que tantear
aumentando el número de chorros; de
esa forma aumenta el diámetro de la
rueda. Hay que tener en cuenta que el
número máximo de chorros es de seis
y con rueda horizontal (de eje vertical).
Entre los valores de las tablas 2 y 3
tomaremos el más cercano al de n que
hemos tanteado en la fórmula (1) y sustituiremos
en la fórmula (43). De esta
forma se obtiene el número específico
de revoluciones y las revoluciones del
eje de la turbina.
Las revoluciones de la turbina coincidirán
exactamente con uno de los
escalones enunciados, ya que en estas
turbinas, por regla general, el generador
va acoplado directamente al eje.
También se puede utilizar la fórmula
(49) para tantear el número de
chorros j.
Con todos estos datos se puede dar
por completado el diseño preliminar de la turbina. Las dimensiones de la
carcasa serán:
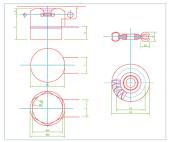
Las dimensiones calculadas en las
fórmulas anteriores, se pueden ver en
la figura 2.
Dado que la resolución puede ser
delicada, se incluye un ejemplo a continuación.
Se resaltan en amarillo los
campos elegidos en el cálculo
Salto H = 252,00 m
Revoluciones = 500 rpm
Potencia P = 1.779,9 Kw
Caudal Q = 0,80 m3/s
Rendimiento = 0,90
Chorros = 3
Velocidad de embalamiento Nr
una serie de valores discretos que van
fijados por el número de pares de polos
del generador y por la frecuencia de la
red. El número de revoluciones n se
mueve en una serie discreta de valores
marcados por la frecuencia de la red y
que son función de la misma, se pueden
ver en las tablas 2 y 3.
Las revoluciones de la turbina coincidirán
exactamente con uno de los
escalones enunciados si el generador
va acoplado directamente al eje, o no,
si el generador se conecta a la turbina
por medio de una multiplicadora.
En el caso de las turbinas Kaplan, es
más fácil hacer coincidir el valor de
n porque los escalones de velocidad
están muy cercanos unos de otros, al
contrario que al principio de la tabla,
que presenta espacios mucho mayores
entre valores contiguos.
Con estos valores se puede realizar
un diseño aproximado del edificio y de
sus condicionantes como el tubo de
aspiración, la altura, etc., pues no diferirán
mucho de los valores reales de ejecución, pues se están rehabilitando
saltos antiguos, donde todavía existen
turbinas de principios del siglo XX.
Como antiguamente muchas piezas se
realizaban de fundición, hay que analizar
por separado el rodete y el caracol,
en el caso de la turbina Kaplan, pues
en diversos casos, se utilizó una carcasa
tipo, que estaba sobredimensionada
para aprovechar un molde preexistente.
En estos casos, si no se analizan por
separado carcasa y rodete, el resultado
es incongruente. Las pérdidas de la
turbina serán inferiores a lo esperado
para una turbina de su tamaño y, por
lo tanto, su rendimiento será algo superior.
Normalmente, el rodete habrá
que sustituirlo, lo que permite la opción
de recalcularlo y de mejorarlo ligeramente.
Sin embargo, lo normal es
que distribuidor y la carcasa se puedan
aprovechar, especialmente esta última.
El inyector o inyectores se podrán
aprovechar muy probablemente.
Bibliografía
Cuesta Diego, l.; Vallarino Cánovas del Castillo, e.;
Aprovechamientos hidroeléctricos, Madrid, 2000.
Grupo Formación Empresas Eléctricas, Centrales
hidroeléctricas II. Turbinas hidráulicas, Madrid,
1994.
Gutiérrez del Villar, M.V., Valverde Barrero, P., González
García, F.J., López Aguado, C.J. y otros, Energías
renovables, CADE, Valladolid, 1999.
Jarabo Friedrich, F. y Elortegui Escartín, N., Energías
renovables, Madrid, 2000.
Layman’s guidebook on how to develop a small hydro
site, Comisión de las Comunidades Europeas,
1995.
Larreategui, A.; Peñalva, I.; Máquinas hidráulicas.
áBACOS”, Curso 2010-2011, E.T.S.I., U.P.V.,
Bilbao, 2010.
Manuales de energías renovables, Minicentrales
hidroeléctricas, I.D.A.E., Madrid, 1996.
Marchegiani, Ariel R.; Metodología de diseño preliminar
para pequeñas turbinas de reacción, VII Encuentro
latinoamericano en pequeños aprovechamientos
hidroenergéticos, Lima, 1997.
Mataix, C., Mecánica de fluidos y máquinas
hidráulicas, Madrid, 1970.
Moulan, PH. Tratado de Mecánica Industrial,
Barcelona, 1924.
Pequeñas centrales hidráulicas, CDTI, Madrid, 1982.
Renewable Energy Yearbook, IDAE, Madrid, 1994.
Selecting Hydraulic Reaction Turbines, Bureau
of Reclamation, A Water Resources Tecnical
Publication, Engineering Monograph, Denver,
1976.
Sintes Olives, F.F., Vidal Burdis, F. La industria eléctrica
en España, Barcelona, 1933.
Zapico Gutiérrez, P. Predimensionamiento de turbinas
Francis, Energética XXI, Madrid, 2014.
Zoppetti, G. Centrales hidroeléctricas, México D.F.,
1982.





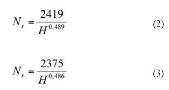
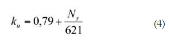
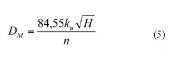









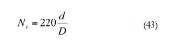

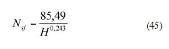

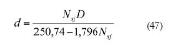






ME PARECE MUY TÉCNICA Y OPORTUNA ESTA INFORMACIÓN, GRACIAS