Optimización topológica aplicada al diseño de componentes plásticos inyectados reforzados con fibra corta

Juan Antonio Almazán Lázaro (1), Ángel López Liñán (1), José Ángel Moya Muriana (1), Carmelo Latorre Castilla (1)

Resumen
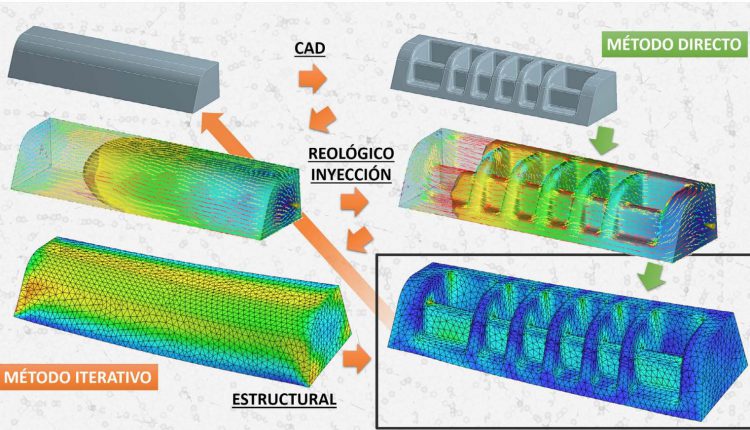
El desarrollo experimentado por los modelos discretos de cálculo basados en el método de los elementos finitos se ha visto acompañado de un auge en las soluciones de optimización topológica estructural. Maximizar la rigidez con la mínima masa es el principal hito que conseguir por parte de los diseñadores. Las restricciones propias del proceso de fabricación en componentes inyectados, como el rango admisible de espesores y el ángulo de desmoldeo, permiten obtener diseños cercanos al componente final cuando se utilizan materiales isótropos. Sin embargo, la no isotropía propia de un material reforzado con fibra corta implica la realización iterativa de fases de optimización, diseño, análisis reológico y validación mecánica, dado que la orientación de fibra es inicialmente desconocida y, a su vez, depende de la solución topológica adoptada. En este trabajo se muestra cómo la implementación de un algoritmo de diagnóstico de espesores permite predecir la orientación de fibra local y optimizar de acuerdo con propiedades mecánicas definidas direccionalmente. Al integrarse en el proceso de optimización, se reduce el número de iteraciones necesarias para alcanzar un modelo mecánicamente válido.

Palabras clave: Optimización, topológica, fibra, simulación, automoción, plástico, Método Elementos Finitos

Abstract
The development experienced by discrete calculation models based on the finite element method has been accompanied by a boom in structural topological optimization solutions. Maximizing stiffness with minimal mass is the main milestone for designers to achieve. The restrictions of the manufacturing process in injected components, such as the admissible range of thicknesses and the demoulding angle, allow to obtain designs close to the final component when using isotropic materials. However, the non-isotropy inherent to a short fiber reinforced material implies the iterative performance of optimization, design, rheological analysis and mechanical validation phases, since the fiber orientation is initially unknown and, in turn, depends on the adopted topological solution. This work shows how the implementation of a thickness diagnostic algorithm allows predicting local fiber orientation and optimizing according to directionally defined mechanical properties. By integrating into the optimization process, the number of iterations required to reach a mechanically valid model is reduced.

Keywords: Optimization, topology, fibre, simulation, automotive, polymer, Finite Element Method.

---

Recibido / received: 09/06/2021. Aceptado / accepted: 15/10/2021.
1 Dpto. de Ingeniería, Centro Tecnológico del Plástico, Fundación Andaltec I+D+i.
Autor para correspondencia: Juan Antonio Almazán Lázaro. ingenieria@andaltec.org

---

Introducción
Dado que los recursos disponibles en la naturaleza son limitados, es de vital importancia usarlos de la manera más eficiente posible. En este sentido, la optimización, que puede ser simplemente definida como el proceso de búsqueda de la mejor solución, representa una valiosa herramienta para conseguirlo, y constituye, por definición, una de las bases fundamentales de la ingeniería. La optimización estructural trata de generar el mejor planteamiento para una estructura que satisface al mismo tiempo varias condiciones impuestas, restricciones de fabricación o resistencia, y objetivos, como utilizar la mínima cantidad de material. Ello permite al sector industrial minimizar el uso de recursos y su impacto ambiental, y a las compañías, ser más competitivas tecnológicamente.

Las variantes de procesos optimización estructural pueden ser clasificadas en tres grandes categorías: paramétrica, de forma y topológica. La optimización paramétrica, el enfoque más simple y temprano, consiste en encontrar el diseño óptimo modificando variables de tamaño, como dimensiones de la sección transversal en barras y vigas, o el espesor en placas [1]. La optimización de forma se aplica principalmente a estructuras continuas, donde lo desconocido es la forma o el contorno de alguna parte del límite de un dominio estructural; modificando esos límites predeterminados se consigue el diseño óptimo [1,2]. Y por último, la optimización topológica, que puede ser clasificada en dos categorías en función del tipo de estructura [3]: a) optimización de estructuras discretas y b) optimización de estructuras continuas. La optimización topológica de estructuras discretas trata con estructuras reticulares como cerchas, emparrillados y panales; optimizando simultáneamente la topología (conectividad de los elementos), geometría (localización de las uniones) y tamaño (dimensiones de la sección transversal). Por otra parte, la optimización de estructuras continuas tiene como objetivo el encontrar el diseño óptimo mediante la selección de la mejor localización y geometrías de cavidades (huecos) en el dominio de diseño, mediante una variable similar a la densidad, que puede llevar cualquier valor, como la masa o la rigidez, a cero. Alternativamente, los elementos de una estructura, como los elementos finitos (FE) utilizados para representarla, se pueden eliminar o agregar al dominio.

En comparación con otros tipos de optimización estructural, la optimización topológica de estructuras continuas es, con diferencia, la más desafiante técnicamente. Sin necesidad de conocer la forma o el tamaño de la estructura, la optimización topológica permite crear diseños conceptuales inéditos y muy eficientes para estructuras continuas. Las técnicas de optimización topológica no solo se pueden aplicar a estructuras a gran escala [4,5], sino que también se pueden usar para diseñar materiales a niveles micro y nano [6-8]. La optimización topológica de estructuras continuas ha cobrado gran interés desde la presentación del método de homogeneización por parte de Bendsoe y Kikuchi [9], aunque su origen se remonta al mínimo peso de las estructuras de Michell [10]. En su formulación original, Michell se ocupó de la topología de barras de menor volumen con una sola condición de carga y una restricción de tensión. La mayoría de métodos numéricos disponibles actualmente para estructuras continuas están basados en análisis de elementos finitos (FEA) en el que el dominio de diseño se discretiza en una fina malla de elementos. En tal configuración, el procedimiento de optimización consiste en encontrar la topología de una estructura determinando para cada punto en el dominio de diseño si debe haber material (elemento sólido) o no (elemento vacío), esto es, a) la propiedad elástica del material, en función de su densidad, puede variar en todo el dominio de diseño, y b) el material puede eliminarse permanente del dominio de diseño.

Para la optimización topológica pueden encontrarse diversos métodos que pueden ser agrupados en dos categorías [11]: a) métodos de criterios de optimidad y b) métodos heurísticos o intuitivos. Los primeros son métodos indirectos de optimización que satisfacen un conjunto de criterios relacionados con el comportamiento de la estructura, mientras que los métodos heurísticos son derivados de la intuición, de la observación de procesos ingenieriles o de la observación de sistemas biológicos. Los métodos criterios de optimidad, a menudo, están basados en la condición de optimización Kuhn-Tucker [12], lo que les otorga gran rigurosidad. Estos son adecuados para problemas con un alto número de variables de diseño y algunas restricciones. Se pueden clasificar en: a) Homogenization [9,13,14], b) Solid Isotropic Material with Penalization (SIMP) [13,15,16], c) Level Set Method [17-19] y d) Growth Method for Truss Structures [11]. En cambio, los métodos heurísticos no siempre garantizan la optimización, pero pueden proporcionar soluciones eficientes viables. En estos, destacan los siguientes métodos: a) Fully Stressed Design [12], b) Computer-Aided Optimization (CAO) [20,21], c) Soft Kill Option [22], d) Evolutionary Structural Optimization (ESO) [23,24], e) Bidirectional ESO (BESO) [25] y f) Sequential Element Rejection and Admission (SERA) [11].

En las últimas décadas, el incremento de capacidad de computación y las rápidas mejoras en los algoritmos utilizados para la optimización han transformado el campo de la optimización estructural, pasando de un interés principalmente académico a la actualidad, en la que lleva a un creciente número de ingenieros y arquitectos a beneficiarse de las técnicas de optimización. Numerosos proyectos de investigación y desarrollo han permitido que los algoritmos de optimización estructural y los paquetes de software estén disponibles para usuarios finales de manera sencilla, precisa, eficiente y económica [1]. Así, muchos de estos códigos han llegado a ser implementados en la mayoría de programas comerciales de análisis estructural como ABAQUS [26], ANSYS [27], FEMtools [28] y Nastran [29]; software específicos como OPTISTRUCT [30], CATOPO [31], y herramientas como TOPOPT [32], CalculiX [33] y SALOME [34]. Todas ellas permiten resolver problemas de optimización de alta complejidad incorporando escenarios de carga múltiple y teniendo en cuenta diversos requerimientos de diseño multidisciplinar.

Aunque es muy amplia la casuística que permite resolver la optimización topológica, los diseños obtenidos deben ser fabricados mediante alguno de los procesos conocidos actualmente, los cuales imponen distintas restricciones que hay que tener en cuenta. El moldeo por inyección es una de las operaciones de procesamiento de polímeros más utilizadas en la industria del plástico actual, en la que más de un tercio de los materiales termoplásticos están moldeados por inyección y más de la mitad de todos los equipos de procesamiento de polímeros son para moldeo por inyección [35]. Representa más del 70% de la producción entre los componentes de los productos de consumo [36]. Permite la obtención de formas complejas con estrictos requerimientos dimensionales y tiempos de ciclo muy cortos [37].

Este trabajo, basado en la optimización de componentes de plástico, trata de mostrar una metodología que complementará a las actuales, con el objetivo de desarrollar tales herramientas cuando se aplican a materiales reforzados con fibra corta.

Optimización topológica aplicada a componentes plásticos inyectados

Generalidades
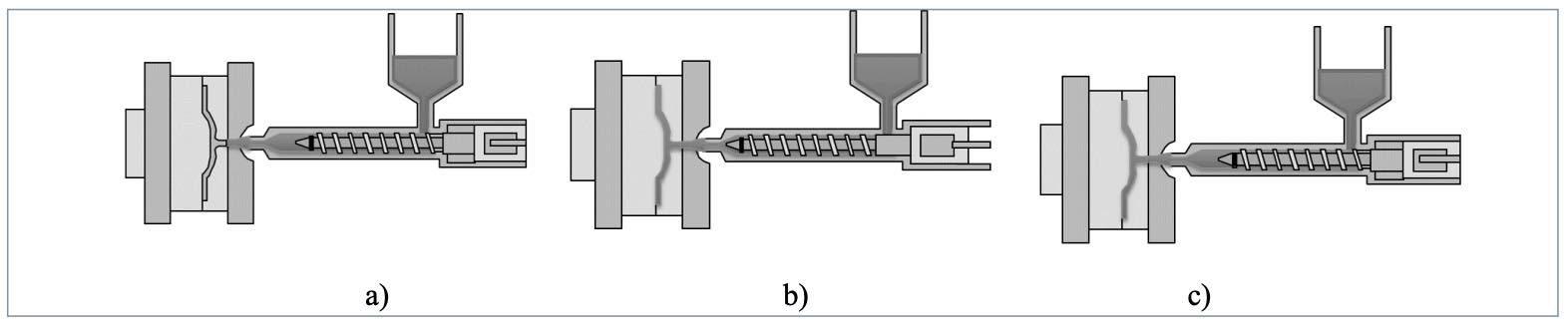
Dada la propia naturaleza del proceso de inyección, la optimización de componentes plásticos queda intrínsecamente ligada al proceso, en el que las propiedades de material final dependen, a su vez, de las condiciones del proceso. El proceso de inyección de plásticos puede ser definido como la sucesión de tres etapas [38,39]: a) calentamiento del material, b) inyección y c) solidificación del polímero fundido, según se resumen en la fgura 1. En primer lugar, la materia prima se calienta a una temperatura próxima a su temperatura de fusión. Posteriormente, el polímero fundido se inyecta en la cavidad a alta presión a través de un sistema de alimentación, para, finalmente, cuando el llenado de la cavidad está casi completado, mantener una presión de compactación durante la fase de efriamiento. En términos generales, el molde consiste en una cavidad o cavidades, conectadas entre sí y a canales de alimentación que dirigen hasta ellas el flujo de masa fundida desde la boquilla de la máquina inyectora.

Son numerosos los factores que contribuyen a las propiedades finales de las piezas inyectadas. Entre ellos, hay cuatro fundamentales: a) el diseño de la pieza, b) el diseño del molde, c) el material y d) los parámetros del proceso. El efecto individual y la interacción de estos factores pueden conducir a diferentes defectos en el componente final, como contracción no uniforme, alabeo, rechupes, líneas de soldadura, falta de llenado o atrapamientos de aire, entre otros. Concretamente, y como punto fundamental de este trabajo, el diseño de la pieza debe atender a los requerimientos dados por las reglas de diseño y limitaciones del proceso y garantizar así la calidad final del componente. Con objeto de facilitar la viabilidad tecnológica de fabricación junto con otros requerimientos económicos y de eficiencia, varios criterios o limitaciones deben aplicarse durante la fase de optimización del dominio de diseño del elemento a inyectar. El espesor de pared de la pieza supone una de las restricciones más importantes que hay que tener en cuenta, pues influye de manera destacada en las propiedades del componente, incluido el rendimiento mecánico, el aspecto estético, la capacidad de moldeo y el coste. El espesor óptimo es, a menudo, un equilibrio entre tendencias opuestas, como la resistencia frente a la reducción de peso y la durabilidad frente al coste.

Así, en secciones simples de pared plana, un aumento del 10% en el grosor de la pared puede suponer, aproximadamente, un aumento del 33% en la rigidez [41,42]. Sin embargo, el aumento del grosor de la pared también conlleva intrínsecamente un aumento del peso, del tiempo de ciclo e incremento por coste de material. Por el contrario, una reducción del espesor puede originar paredes excesivamente delgadas que pueden provocar altas velocidades y presiones de inyección e, incluso, la imposibilidad del llenado completo de la cavidad debido a la solidificación prematura del material fundido. El moldeado de pared delgada (menos de 1,5 mm) generalmente es más adecuado para reducir el tamaño y el peso que para ahorrar costes.

Los nervios proporcionan un medio para aumentar económicamente la rigidez y la resistencia sin aumentar el espesor general de la pared. El diseño adecuado de nervios involucra cuatro aspectos principales: espesor, altura, ubicación y cantidad. Los nervios gruesos, a menudo, causan rechupes y problemas de aspecto en la superficie que los contiene y nervios muy delgados pueden dificultar el llenado. Para evitar problemas de llenado, ventilación y expulsión del molde, las reglas estándar limitan la altura del nervio en función del grosor de su superficie base, además de mantenerse suficientemente separado para conseguir un enfriamiento adecuado del molde.

Otra condición a tener muy presente durante los ciclos de desarrollo de la optimización es el eje de desmoldeo y el ángulo asociado al mismo, pues al proporcionar dicha dirección estamos aleccionando a que la mayoría de paredes, nervios, torretas y refuerzos respeten dicha dirección de construcción. Cualquier otra dirección de trabajo en el molde, conocida como negativos, obligará a dotar de elementos auxiliares (correderas, patines, etc.) el utillaje e implicará un aumento en el coste del mismo.

Algoritmos e implementaciones
El problema de optimización topológica de medios continuos radica en encontrar la mejor distribución de material (función objetivo) dentro del dominio de diseño, de tal forma que el componente resultante maximice algún tipo de cumplimiento mecánico (respuesta) bajo ciertas restricciones. La optimización topológica puede consistir en minimizar una función objetivo (normalmente el volumen total de la estructura, masa o coste) sujeta a la respuesta sobre la estructura (tensiones, desplazamientos, cargas de pandeo, frecuencia natural, etc.). Adicionalmente, las restricciones pueden derivarse del proceso de fabricación.

Múltiples son los algoritmos actuales de optimización topológica que aceptan restricciones de proceso y, por tanto, su aplicación al diseño de piezas fabricadas por inyección. Entre ellos destacan: a) Solid Isotropic Material with Penalization (SIMP), b) Level Set y c) BESO (Bidirectional Evolutionary Structural Optimization).

El método SIMP [13,15,16] fue desarrollado como consecuencia directa del método de homogeneización. La idea es usar solo una variable de diseño por elemento finito. Esta variable de diseño es una densidad de elemento artificial (?e) con cualquier valor dentro del rango 0 < ?min ? ?e ? 1. Ello derivaen que el volumen de un elemento se multiplica por esta densidad artificial para producir su volumen real, por lo que el volumen del dominio del diseño viene dado por:

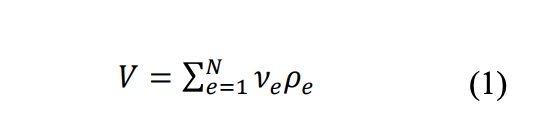siendo N el número total de elementos finitos usados para representar el dominio de diseño, v_e y p_e  el volumen y densidad artificial de cada elemento, respectivamente, y V el volumen resultante del dominio de diseño. En esta técnica, las propiedades del material en cada elemento se asumen constantes y una penalización (p) es aplicada sobre la densidad cuando se multiplica por el módulo elástico:

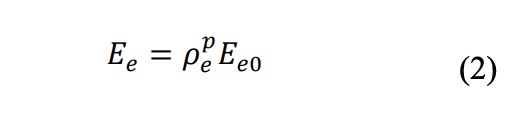(2) donde E_e0  es el módulo elástico original del material, E_e es el nuevo módulo elástico artificial de cada elemento y p es una potencia de penalización que convierte los valores intermedios de densidad en valores discretos (0-1), para así conseguir únicamente elementos sólidos o vacíos. Con el proceso de optimización ejecutándose de forma iterativa, inicialmente con p = 1, el valor óptimo es calculado; este es incrementado y la optimización se repite hasta que un diseño es generado:

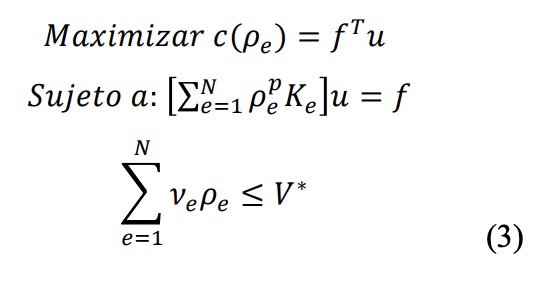donde f y u son los vectores de carga y desplazamiento; c cumplimiento medio; K matriz de rigidez; y V^* límite superior de volumen establecido.

El método Level Set es otra técnica que trata directamente con el límite estructural de las formas, y en ella, el límite de diseño se representa implícitamente como la isosuperficie (conjunto de nivel cero) de una función ?(x) definida en la malla de elementos finitos [19]. El dominio se especifica respecto al valor de la función de conjunto de niveles:

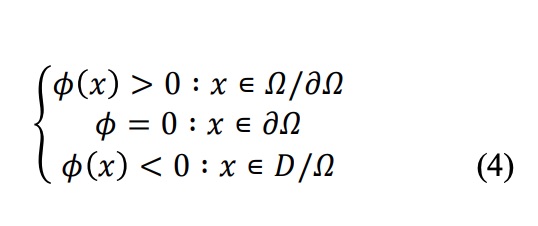donde D es el dominio de diseño; ? la región con material, ?? representa el límite y D/? la región sin material. El movimiento dinámico del límite se rige por la llamada ecuación de Hamilton-Jacobi:

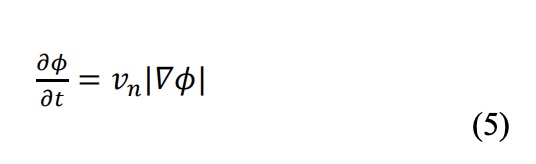donde v_n es la velocidad normal del límite estructural y |??| es la norma del gradiente de la función de ajuste de nivel. La idea básica de la ecuación del conjunto de niveles es mapear la evolución del límite en una evolución de la función del conjunto de niveles ?(x)

En cambio, en el método BESO [25], la estructura se optimiza eliminando y agregando elementos. Es decir, el elemento en sí, en lugar de sus parámetros físicos o materiales asociados, se trata como la variable de diseño. El problema de optimización con la restricción de volumen se establece como:

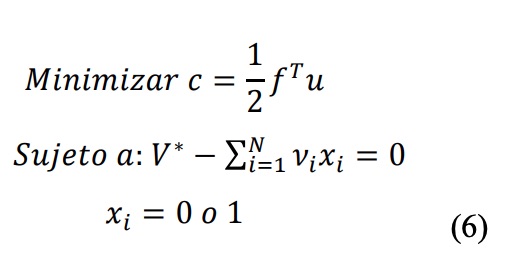declarando la variable de diseño binario [_i la ausencia (0) o presencia (1) de un elemento.

La mayoría de los trabajos de optimización estructural están relacionados con el diseño óptimo de estructuras con material isótropo. Extender los métodos de optimización a aplicaciones que involucran heterogeneidad de material (p. ej., por adición de refuerzo en forma de fibra) supone un avance en su desarrollo.

Efecto del refuerzo por fibra corta
A pesar del extendido uso de los polímeros en multitud de sectores debido a su bajo coste de producción y elevada cadencia, su baja rigidez y resistencia suponen un aspecto negativo que puede limitar en gran medida su utilización. Para eludir estas limitaciones se recurre a otros materiales o al incremento de dicha rigidez y resistencia mediante el uso de refuerzos, y así, en los componentes fabricados mediante procesos de inyección este refuerzo suele tomar la forma de partículas o fibras.

La causa de utilizar preferentemente un refuerzo en forma de fibra, y no de otra forma geométrica, obedece al hecho de que a causa del reducido diámetro de estas (del orden del tamaño de un cristal de la estructura cristalina del material utilizado) se consiguen dos efectos relevantes: reducir las posibilidades de que haya algún defecto a lo ancho de dicha fibra y que su estructura quede orientada con el eje de la misma. De esta forma, se consiguen resistencias muy superiores a las del propio material en bruto con el que se ha fabricado dicha fibra [43]. Tal es el caso de la fibra de vidrio (una de las más utilizadas) que en forma de fibra presenta una resistencia a la tracción de 3,5 GPa mientras que el vidrio en bruto difícilmente supera 1 GPa [44].

Como contrapartida, una característica intrínseca a que el refuerzo tenga forma de fibra es que su efecto de aporte mecánico se produce principalmente en la dirección de esta, mientras que su contribución a la rigidez y resistencia en dirección radial a la misma es insignificante, lo que da lugar en el compuesto a un comportamiento mecánico ortótropo muy marcado por dichas direcciones. A esto hay que añadir que durante el proceso de inyección la fibra queda orientada en función de múltiples parámetros intrínsecos al proceso, como el movimiento del fluido durante el llenado, su viscosidad, vorticidad, velocidad de deformación y forma de la propia fibra.

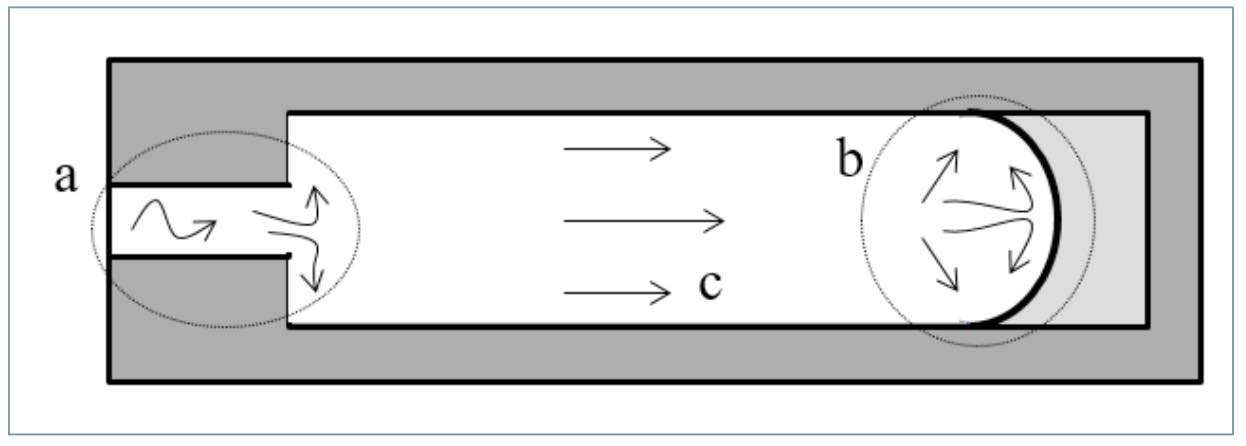
Así, durante la fase de llenado de un molde se distinguen tres tipos de flujo que determinan en gran medida la distribución final de la fibra según se muestra en la fi gura 2. Distintos tipos de flujo se desarrollan en las diferentes secciones: a) flujo tridimensional y turbulento cerca de la entrada, por lo que la fibra en esta zona no presenta una orientación definida; b) tipo fuente en el frente de flujo, y c) entre ambas zonas, flujo viscoso con un campo de velocidad uniforme y paralelo al flujo. En esta zona, el flujo de tipo viscoso contribuye a dar una orientación determinada a la fibra muy dependiente de la dirección del flujo e influenciado por el espesor de la pieza.

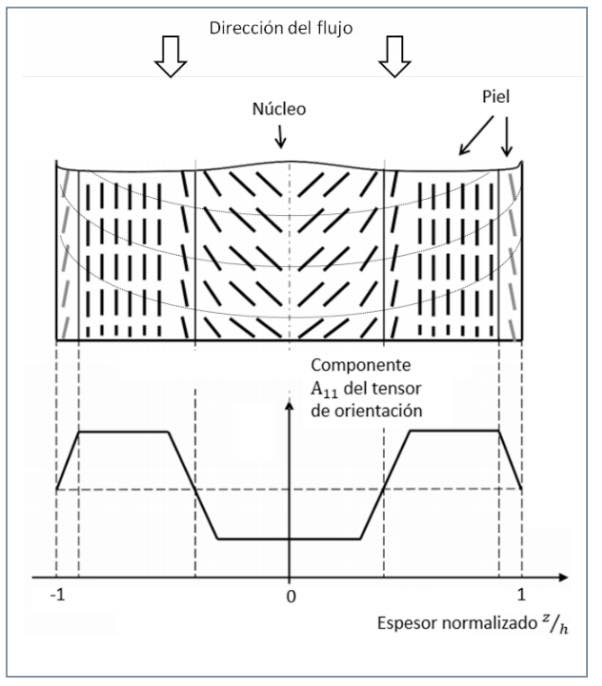
Además del tipo de flujo y su dirección durante el llenado, el proceso de solidificación al entrar en contacto el material fluido con las paredes relativamente frías del molde da lugar a una variación de la direccionalidad de la fibra dentro del propio espesor de la pieza. Así, por el contacto del fluido con las paredes del molde se forma una primera capa solidificada de material (conocida como piel) en la que, a su vez, se diferencian dos zonas: por un lado una delgada capa límite adyacente al molde, donde el flujo no se ha desarrollado y, por tanto, la fibra no muestra una orientación preferente y queda de forma aleatoria y, por otro, el resto de capa solidificada donde la fibra tiende a quedarse orientada paralela a la dirección del flujo.

Por otra parte, el resto de material fluido y en movimiento (zona conocida como núcleo) da lugar a una orientación perpendicular a la dirección del flujo. Así, la orientación de la fibra y, por tanto, las propiedades mecánicas locales, no son homogéneas a lo largo del espesor, lo que muestra diferencias más acentuadas a medida que aumenta el espesor [45]. Estas diferencias se vuelven menos acentuadas a medida que aumenta la cantidad de fibra [46]. Consecuentemente, a lo largo del espesor queda una distribución de fibra como la mostrada en la fgura 3 [47].

Por último, hay que añadir que durante el proceso de inyección, parte de las fibras se rompen, por lo que se reduce su longitud. Si su longitud no es la suficiente como para permitir a la fibra ejercer todo su papel de refuerzo, situación conocida como fibra corta, se estarán también limitando sus propiedades mecánicas potenciales [44].

En este contexto se plantea un escenario en el que prácticamente en cada punto de la pieza se tiene una orientación diferente de fibra y, por tanto, también un comportamiento no isótropo específico diferente.

Sin embargo, todos estos factores pueden ser tenidos en cuenta para determinar con precisión la orientación de la fibra en cada punto de una pieza haciendo uso de software específico para el estudio de inyección de plásticos, como Autodesk Moldflow [48], que reproduce el proceso de inyección mediante técnicas de análisis numérico. A pesar de la elevada precisión que este tipo de estudios permiten en la determinación de la orientación de la fibra en cada uno de los puntos de la pieza, requiere, por un lado, la posterior aplicación de un modelo micromecánico para calcular las propiedades mecánicas a partir de esas orientaciones de fibra, y, por otro, una geometría bien definida sobre la que realizar el estudio de llenado, por lo que durante el proceso de optimización estructural propiamente dicho no son aplicables ni permiten realizar una optimización estructural teniendo en cuenta la orientación final que tendrá la fibra [49].

Así, si se pretende realizar una optimización estructural en la que ya se tenga en cuenta la orientación que tendrá la fibra, se encuentran limitaciones en cuanto a software disponible. A pesar de ello, si los espesores de las piezas inyectadas son lo suficientemente pequeños (geometrías laminares), las direcciones principales del esfuerzo quedarán orientadas en el plano de la misma y, en consecuencia, de forma aproximada, se tendrá un excelente comportamiento mecánico en el plano de la pieza y más reducido en la dirección perpendicular a dicho plano. De esta manera se puede simplificar el cálculo de las propiedades del compuesto y sirve como punto de partida [44]. Gracias a esta distribución de la fibra de manera, aproximadamente, laminar, se pueden determinar las propiedades mecánicas del compuesto partir de sus constituyentes haciendo uso y adaptación del modelo micromecánico de compuestos laminares, ampliamente desarrollado para el sector aeronáutico. Este modelo permite calcular con gran precisión la rigidez de un material compuesto a partir de sus constituyentes. Para ello, se parte de la suposición de que el compuesto forma una lámina unidireccional de reducido espesor con fibras infinitamente largas y alineadas todas en la dirección de la lámina. Posteriormente, es adaptado a fibras de una longitud finita y una orientación no unidireccional.

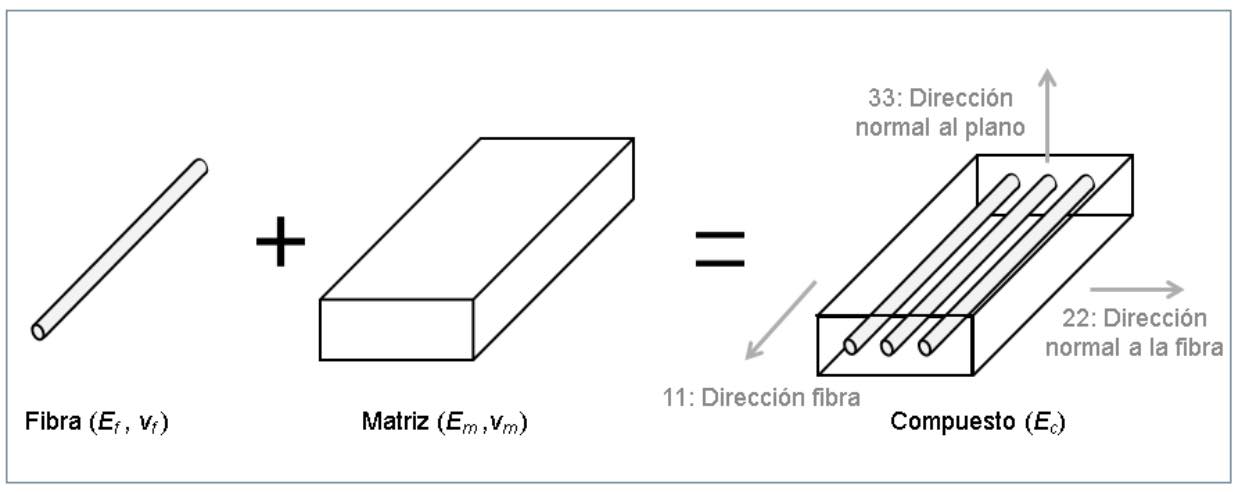
Según el modelo micromecánico descrito en la figura 4, partiendo de las hipótesis de repetitividad en la orientación de la fibra, homogeneidad, isotropía y linealidad tanto en matriz como en la fibra, unión perfecta entre ambas y una proporción de fibras lo más alta posible, tras aplicar las ecuaciones de equilibrio y compatibilidad a un volumen mínimo representativo de fibra y matriz, se tiene la siguiente rigidez del compuesto (subíndice c) en la dirección de la fibra en función de las rigideces (E) y proporción volumétrica (v) de la fibra (f) y de la matriz (m) se puede escribir regla de las mezclas [43]:

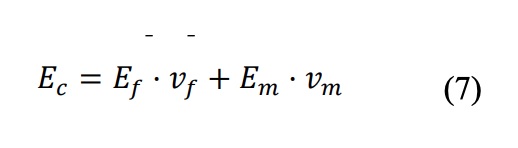De la misma manera, se puede aplicar a la dirección transversal [43]:

Para el cálculo de la rigidez en la dirección de la fibra se han desarrollado numerosas modificaciones semiempíricas de dicha regla. Destaca la modificación realizada por Krenchel [50], que introduce el parámetro K para tener en cuenta la orientación no unidireccional de las fibras, basándose en el ángulo que forman estas con la orientación preferente de la lámina y su sección equivalente en dicha orientación.

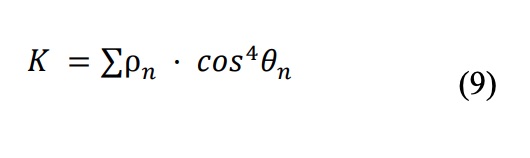donde    representa la proporción

de fibras con orientación ?n sobre el total, y ??! el ángulo que forman estas con la dirección preferente o mayoritaria. Así, se adopta la regla de las mezclas como:

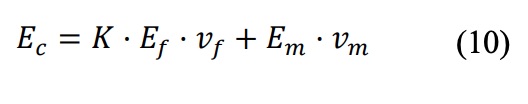donde el valor K es el parámetro de eficiencia de la fibra, que estará dado en función de la orientación preferente de la fibra y de la dirección del esfuerzo, según la tabla 1.

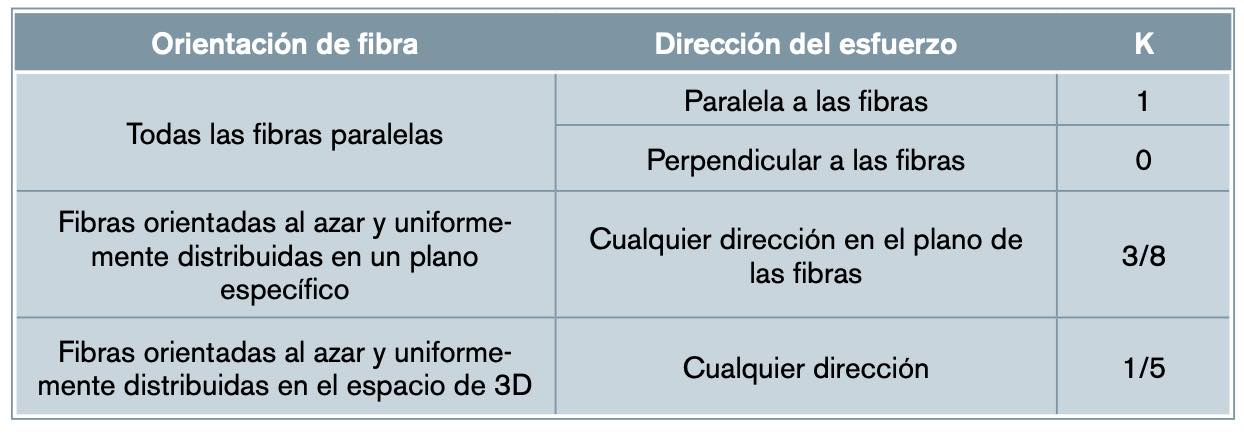
Para el caso de piezas inyectadas de las que desconocemos su orientación de fibra, podríamos partir del supuesto de distribución completamente aleatoria en todas las direcciones, con esto el factor de Krenchel toma el valor de 1/5. Sin embargo, si la geometría es de tipo laminar y tiene un espesor reducido, prácticamente todo el refuerzo queda orientado en el plano de la misma y nada fuera de dicho plano. Así, hacer la aproximación de una distribución nula fuera del plano y aleatoria dentro de él, el factor de Krenchel toma el valor de K=3/8, lo cual supone incrementar las propiedades de rigidez en un factor 1.875 si la fibra se alinea en un plano, en relación con la completamente aleatoria tridimensional. Así, resultaría un compuesto de comportamiento ortótropo con propiedades iguales e influenciadas por el refuerzo en cualquier dirección del plano de la pieza y diferentes, y muy inferiores, en la dirección perpendicular al mismo.

Por otro lado, para este mismo caso, otros autores han realizado diferentes aproximaciones empíricas de la rigidez del compuesto en dicho plano [51]: Aproximación de Cox:

Aproximación de Loewenstein:

Aproximación de Tsai-Pagano

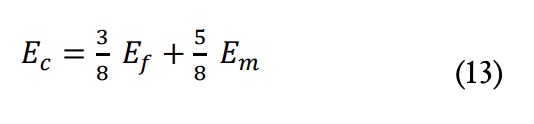Sin embargo, ninguna de estas tres aproximaciones empíricas tiene en cuenta la proporción de fibra y de matriz, dado que suponen que la proporción de fibra es la máxima para dicho compuesto y la matriz es utilizada únicamente para rellenar el hueco entre fibras. Sin embargo, en piezas poliméricas inyectadas, no es posible inyectar proporciones de fibra muy elevadas (raramente superan el 50% del volumen), pues, por un lado, las presiones de inyección serían muy elevadas y, por otro, dejaríamos de estar inyectando un fluido propiamente dicho. Como consecuencia, en este estudio se asumirá el modelo de Krenchel, de aplicación en aquellos casos con bajas proporciones de fibra y que, además, tiene en cuenta la proporción de fibra en el material.

Métodos de implementación del modelo

Generalidades
En este contexto, y como objetivo fundamental de este estudio, se propone una implementación complementaria a la metodología actual anteriormente expuesta con la que pueda reducirse tanto el costo computacional como el número de ciclos requeridos para alcanzar la geometría óptima. Dado que gran parte de los recursos se deben al proceso iterativo de optimización-modelado-validación, especialmente cuando se trata con materiales reforzados con fibra corta, se afronta el problema desde el punto de definición de las propiedades mecánicas.

Según el procedimiento actual, se asigna al material unas propiedades isótropas, dado que la direccionalidad local de la fibra no es conocida. Así, una vez que se conoce la orientación de la misma, es necesario recalcular el modelo utilizando las propiedades ortotrópicas. De manera implícita al proceso de inyección, se produce una orientación predominante de la fibra, de manera que esta queda contenida en planos paralelos a la superficie media del sólido. En estas condiciones, las propiedades en tales planos serán superiores a las transversales.

En la fgura 5 se describe la metodología propuesta mediante un diagrama de flujo. Tras definir y discretizar el espacio de diseño específico para el componente, se aplican sobre el modelo las condiciones de contorno y se definen las variables a maximizar/ minimizar, así como las restricciones impuestas por parte de las especificaciones del proceso y/o producto. En cuanto al material, se aplicarán en el primer ciclo propiedades de rigidez isótropas inicialmente estimadas mediante el modelo de Krenchel anteriormente expuesto.

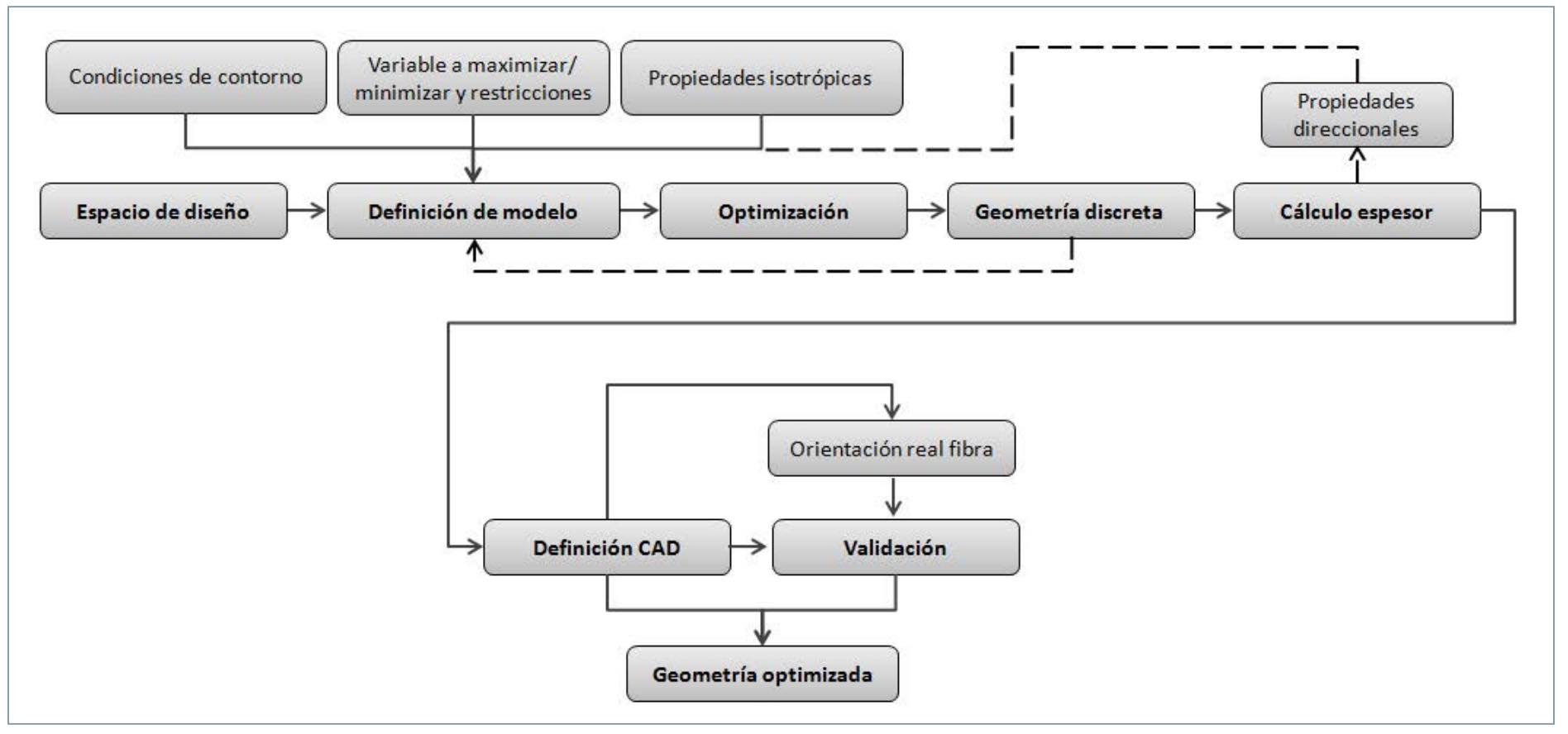
Tras llevar a cabo un proceso de optimización preliminar mediante la aplicación de alguno de los métodos descritos, aplicando el MEF (Método de los Elementos Finitos), y fijado el valor de densidad artificial de elementos, ?e , se obtiene la geometría discreta que cumple con el objetivo y las restricciones impuestas al modelo. A continuación, se realiza sobre esta un cálculo aproximado de espesores mediante el algoritmo propuesto en el punto 4.2, lo cual permite conocer los planos de orientación de fibra locales, así como el espesor local. Conocidos los planos de orientación, se asignan propiedades direccionales locales a cada uno de los elementos del dominio discreto optimizado. Según el modelo de Krenchel y los valores de la tabla 1, conocer los planos de orientación implica la aplicación de un factor K=3/8, en lugar del inicialmente aplicado para fibras espacialmente no orientadas, donde K = 1/5. Adicionalmente, se tendrá en cuenta que, para un determinado espesor, la fibra en capas más externas está mejor alineada con el flujo que aquellas localizadas en el núcleo, según la fgura 3. Esto se tendrá en cuenta en el momento de asignar las propiedades locales. Como consecuencia, las propiedades mecánicas direccionales mejoran en un factor de 1.875, y se puede afirmar que el espacio de diseño obtenido para fibras aleatorias tridimensionales incluirá el resultado que se obtiene cuando se aplican propiedades orientadas en el plano. Por ello, la geometría optimizada obtenida en el primer ciclo puede ser utilizada como espacio de diseño para ciclos posteriores, siempre que estos tengan en cuenta la direccionalidad de los planos.

En la segunda etapa del proceso se define el espacio de diseño como el resultado obtenido del ciclo de optimización anterior, y no se requieren tareas de modelado CAD (Computer Aided Design). Asimismo, se definen las propiedades direccionales en función de las direcciones analizadas según el punto 4.2, mejorando en todos los casos respecto a las propiedades isótropas reducidas definidas en el primer ciclo. Las funciones objetivo, así como las restricciones, se mantendrán según el ciclo anterior. Tras el segundo análisis de optimización, el modelo habrá reducido aún más la masa total y los espesores locales, aunque la orientación de los planos locales no se habrá Figura 5. Diagrama de flujo de la metodología propuesta para optimizar componentes plásticos reforzados con fibra corta. visto afectada. En este punto, teniendo un modelo discreto que atiende a todas las restricciones, cargas y propiedades impuestas, puede procederse con las pautas de elaboración de una geometría continua detallada, de acuerdo con los requerimientos dimensionales, funcionales y estéticos especificados. Finalmente, puede recurrirse a un cálculo final de validación en el que se tendrá en cuenta el análisis de orientación de fibra real (mediante el análisis reológico específico del componente) y la geometría CAD anterior.

Cálculo de espesor, orientación de fibra y propiedades mecánicas locales
Dado que, según se mostró, las propiedades mecánicas son marcadamente dependientes del espesor, se deriva la necesidad de evaluar el espesor local en cada punto de la geometría optimizada, de manera que puedan asignarse las propiedades mecánicas correspondientes a cada elemento en función de su posición a lo largo del espesor.

Justificada la necesidad de calcular el espesor local y asignadas, en consecuencia, las propiedades mecánicas, se ha implementado un algoritmo que permite calcular tales valores, dada una geometría discretizada en forma de elementos. Hay multitud de métodos para la determinación de espesores tanto en geometrías 2D como 3D, como el de la máxima esfera circunscrita, utilizado en distinto software de cálculo [48] o el de lanzamiento de rayos propuesto por Rolland-Nevière et al [52]. En este trabajo, se propone como punto de partida el uso del método híbrido, de lanzamiento de rayos, una dirección coincidente con la normal del elemento, si bien se recurrirá a alguno de los métodos anteriores, de mayor estabilidad y versatilidad cuando se trate de geometrías de gran complejidad.

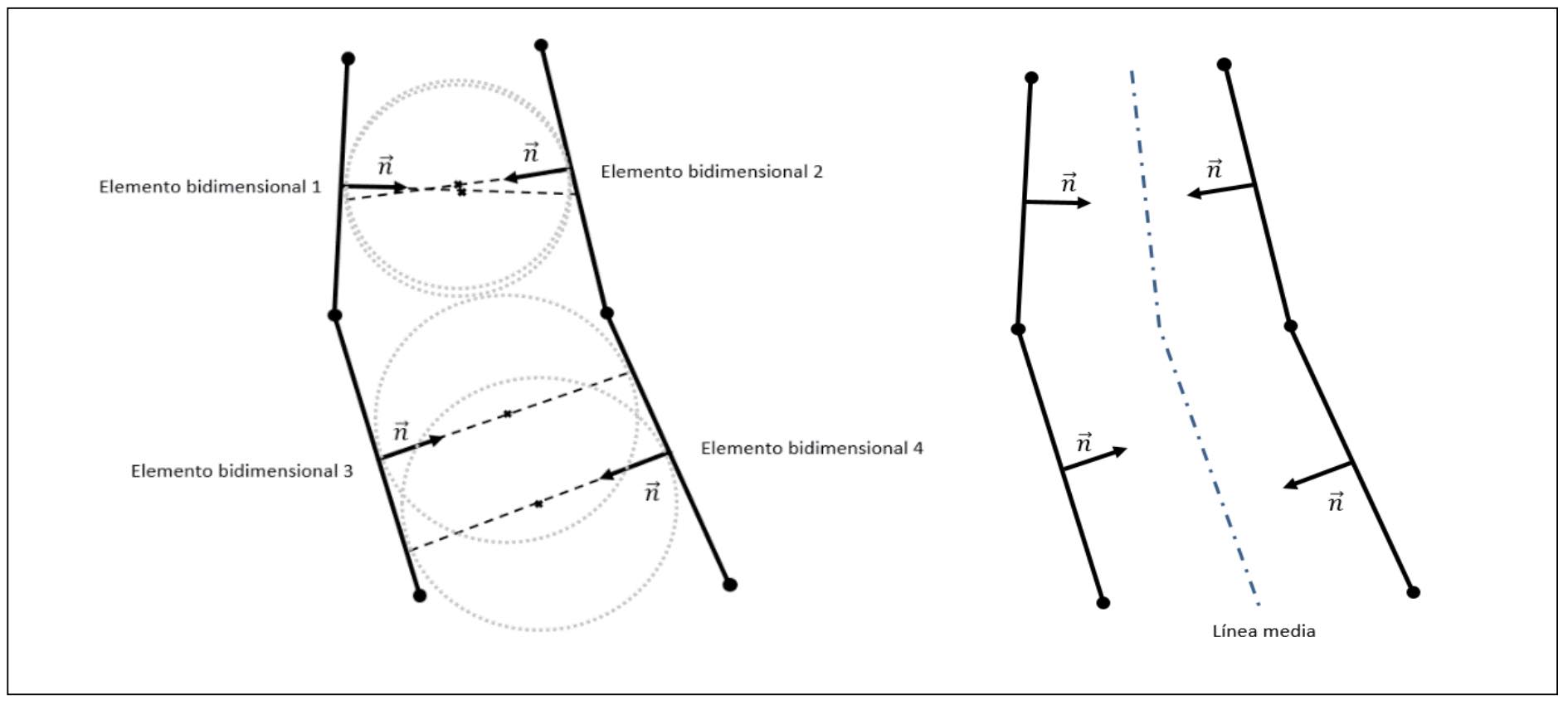
Así, dada una geometría discretizada, el procedimiento de cálculo de espesores simplificado se basa en utilizar la dirección normal de los elementos 2D de la piel externa para encontrar su intersección con el plano definido por elemento al que corte. La distancia entre el origen del vector normal y el plano definirá el espesor local en las inmediaciones del elemento. Llevado a un caso de geometría bidimensional, una vez trazada la normal a un elemento 1D que pase por su centro y encontrado el punto de corte con la línea definida por un elemento enfrentado, se definirá el espesor local como la distancia entre ambos puntos, como se muestra en la fgura 6. La línea trazada entre dos elementos definirá la línea media, que en el caso tridimensional será el plano medio.

El cálculo de las propiedades mecánicas elásticas puede realizarse mediante cualquiera de los modelos anteriormente descritos. Por simplicidad, en este caso se ha utilizado el modelo de Krenchel, asumiendo los valores tabulados en la tabla 1. Para el nivel de resistencia, pueden asumirse, de manera general y desde el punto de vista conservador, los especificados por los ensayos a tracción cuando la dirección de la fibra coincide con la del esfuerzo, y las propiedades de la matriz cuando ambos son perpendiculares. La relación entre ambos dependerá de las propiedades de la matriz, de la fibra y de la fracción de fibra contenida.

Implementación
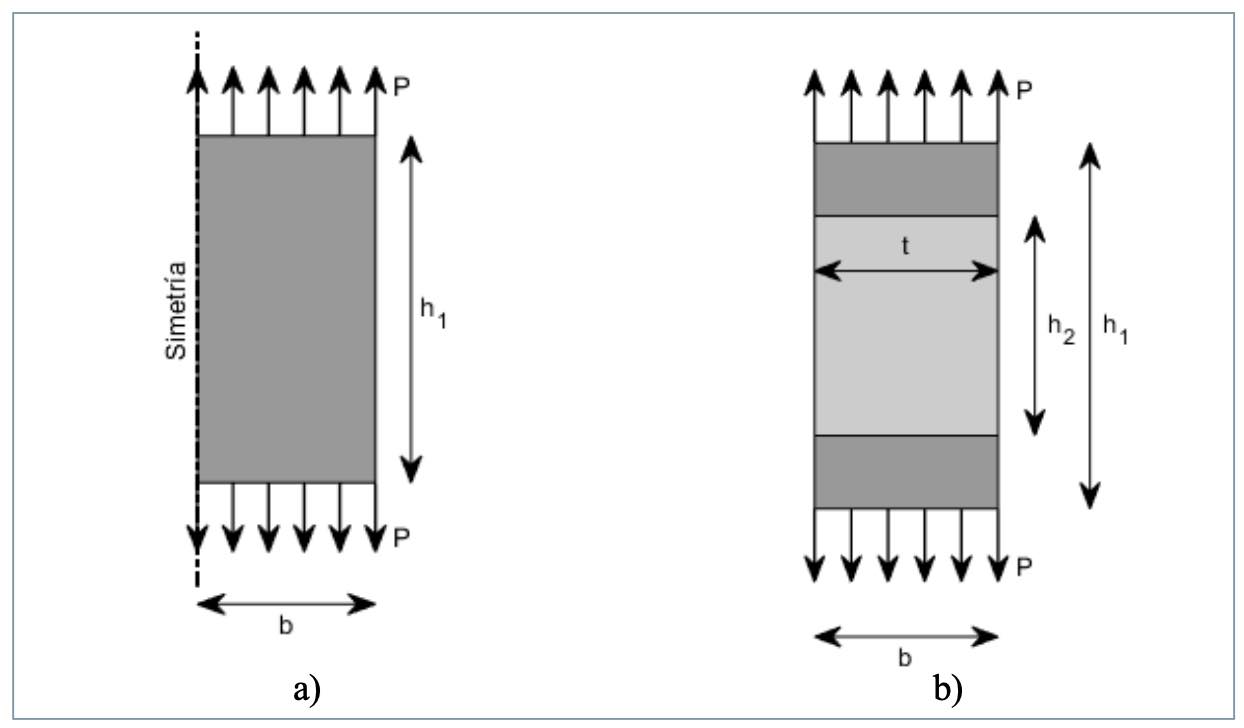
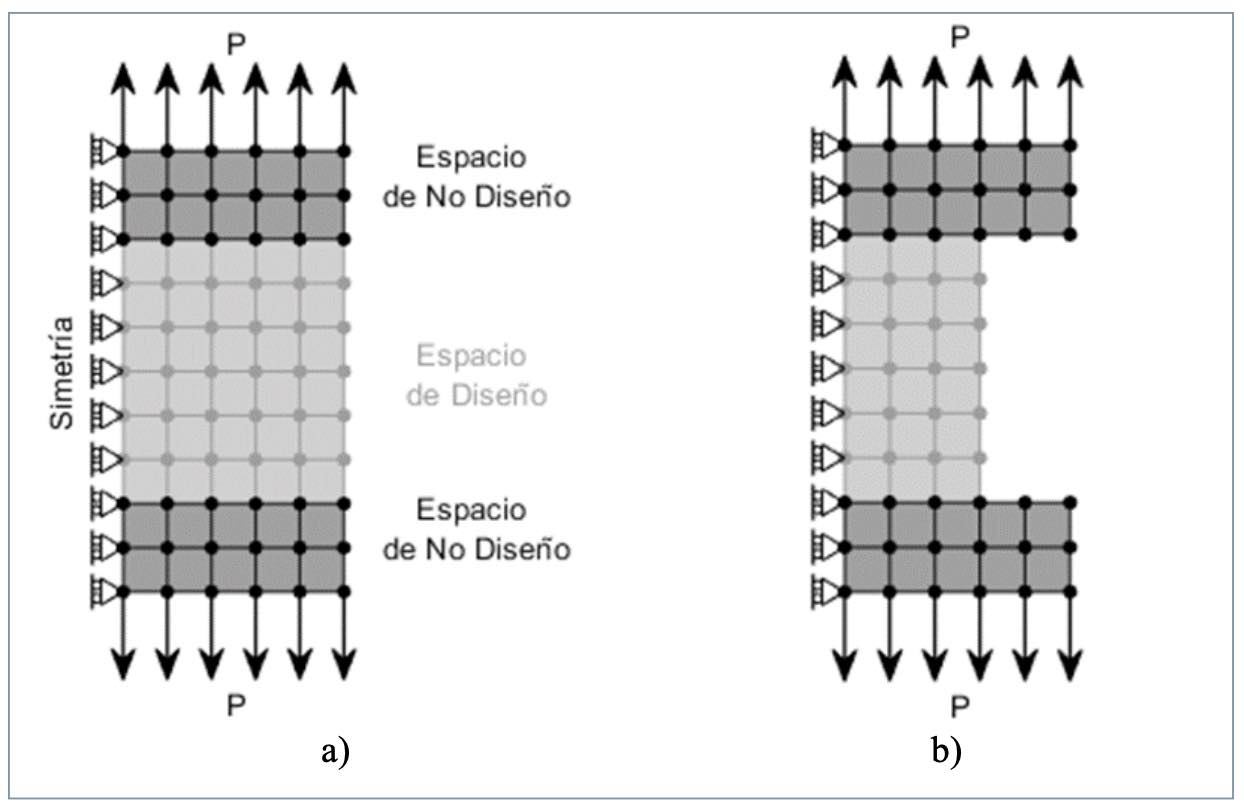
Para llevar a cabo la implementación se ha utilizado un modelo bidimensional sometido, de manera simplificada, a un estado de tracción pura generado por una carga P sobre una probeta simétrica de longitud h y ancho 2b, quedando con una geometría como la mostrada en la fgura 7a. Se asume un espacio de diseño en la zona central, sobre la que se optimizará su espesor, de ancho inicialmente t = b, y dos espacios de no diseño dedicados a la ubicación de las mordazas, según se muestra en la fgura 7b. Dado que se trata de un ejemplo ilustrativo del método, se obvia el efecto de concentración de tensiones, dado que, además, por el reducido número de elementos se asume que cada elemento contribuye con valores de carga admisibles superiores al efecto de la concentración. En la aplicación extensivas, como la mostrada en el punto 5, puede incluirse Rigid Body Element Type 3 (RB3), que distribuya y homogeneice la tensión en los puntos de aplicación de carga y de contorno. Igualmente, una malla de un tamaño suficientemente pequeño permitirá mantener las celdas necesarias para capturar los fenómenos de concentración. Con el mismo objetivo, los códigos de optimización suelen integrar modelos con este fin [30].

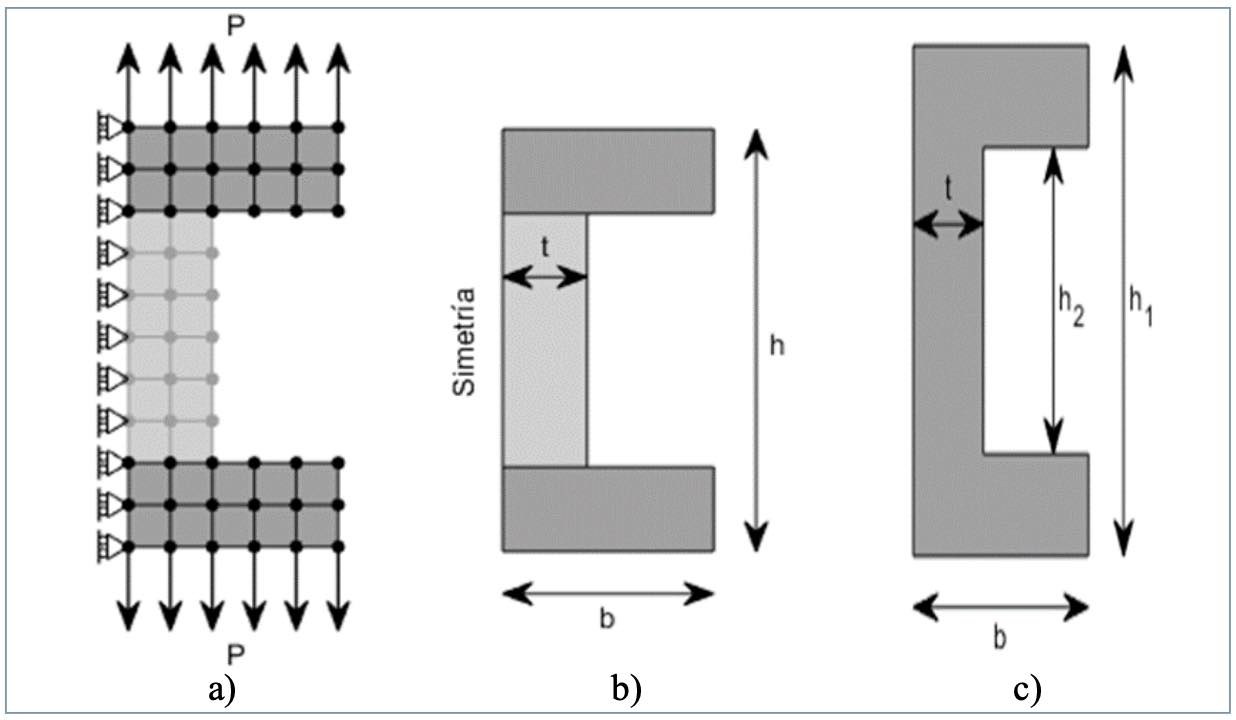
Tras la definición del espacio de diseño y espacio de no diseño (Fig. 8a), se realiza el primer ciclo de optimización, con unas propiedades mecánicas isótropas correspondientes a la fibra aleatoriamente orientada. Se imponen en el modelo, además, las condiciones de contorno propias de la simetría. El resultado es el mostrado en la figura 8b, en la que la sección y la masa del espacio de diseño se han reducido al 60% del inicial.

Una vez redefinido el espacio de diseño obtenido del paso anterior, y aplicadas las propiedades mecánicas locales actualizadas en función del espesor calculado (con K = 3/8), se obtiene la geometría discreta mostrada en la figura 9a, y reconstruida de forma continua en la figura 9b y la figura 9c. El espesor obtenido es, finalmente, t, que supone solo el 40% del inicial.

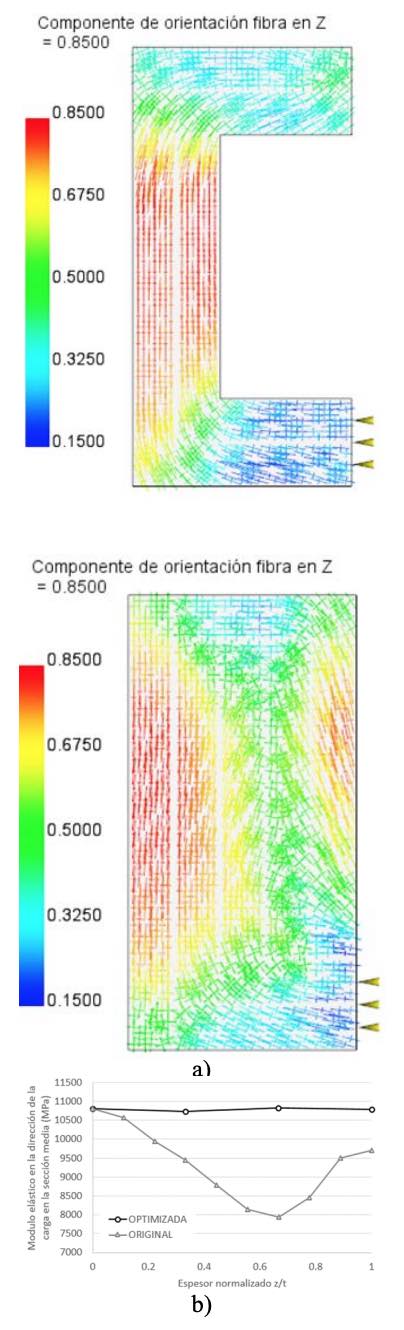
Una vez obtenida la geometría optimizada, la simulación reológica reporta los resultados mostrados en la figura 10a, en la que se corroboran los resultados anticipados con relación a la orientación de fibra cuando los espesores se reducen hasta los valores usualmente utilizados en inyección de materiales poliméricos. Además, en la figura 10b se describe el valor de módulo elástico en la dirección vertical (Z) en función del espesor normalizado z/t. Puede observarse cómo, si no se tienen en cuenta las propiedades una vez optimizada la pieza, se comete un error destacable al imponer las propiedades mecánicas el modelo a optimizar.

Resultados y discusión: aplicación al diseño y validación

Aplicación a modelo de PA6GF30
La validación de la implementación propuesta se apoya en la comparativa de resultados con la metodología actual. Se han tenido en cuenta tanto las características mecánicas finales del conjunto como el tiempo de procesamiento requerido hasta llegar a la solución. Se utiliza OPTISTRUCT como algoritmo de cálculo en ambos casos, que implementa el método SIMP.

Para la aplicación se ha utilizado un caso de diseño específico de un componente de automoción, concretamente un accesorio de arrastre de motocicletas sometido, principalmente, a cargas de tracción y flexión. Como material de diseño se ha utilizado poliamida 66 reforzada con el 35% de fibra PA6-GF35 B3WG7 con las propiedades mecánicas obtenidas de Mortazavian et al. [53] en el estado de condición de humedad. Según el análisis experimental de Mortazavian et al [53], las propiedades a resistencia de la PA6-GF35 se ven incrementadas desde 90 MPa cuando la fibra es transversal al esfuerzo hasta los 150 MPa cuando la fibra está totalmente alineada con la dirección del esfuerzo.

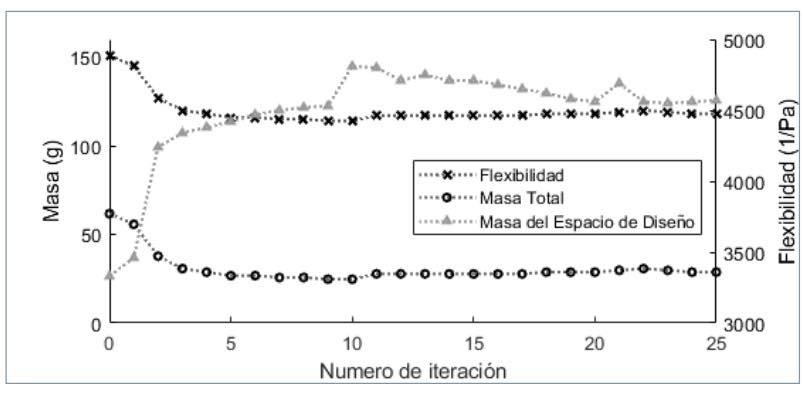
Como punto de partida, se define un espacio de diseño según el indicado en la ifgura 11a, siendo el espacio de no diseño el impuesto por las condiciones de contorno y fijación, así como localización de insertos y tornillería, según se muestra en la figura 11b y en la figura 11c. En las condiciones de contorno como fijaciones, tornillería y puntos de aplicación de carga se añaden elementos de tipo RB3 (Rigid Body Element Type 3) con objeto de distribuir y homogenizar la carga, reduciendo así el efecto de concentración de tensión en tales zonas. El escenario de análisis se basa en una carga puntual de 1.500 N en una dirección que forma 25 grados sobre la horizontal. Como función objetivo se establece minimizar la masa del espacio de diseño mientras que se maximiza la flexibilidad en el extremo. La evolución de ambas variables durante la optimización se muestra en la figura 12, en la que también se ha añadido la masa total de conjunto. A medida que avanza el número de iteraciones, tanto la masa total como la del espacio de diseño decrecen rápidamente, mientras que la flexibilidad muestra un fuerte aumento al comienzo para disminuir ligeramente en el punto de convergencia. Como restricciones, se impone que la tensión máxima no supere la del límite elástico del material, además de limitaciones en los espesores máximos, según el proceso de inyección, fijados entre 2 y 6 mm. Como propiedades mecánicas del primer modelo de optimización se consideran las correspondientes a aplicar K=1/5 en el modelo de Krenchel. Una vez que se obtiene el primer modelo optimizado, en forma de geometría discretizada, se utiliza como entrada en el segundo ciclo de optimización. En este segundo ciclo, las propiedades mecánicas aplicadas corresponden a un factor de Krenchel K=3/8, además de tener en cuenta variaciones locales a lo largo del espesor. Así, en las capas alejadas de la piel, el factor K aplicado es más reducido, dado que la orientación en tales zonas es menos favorable.

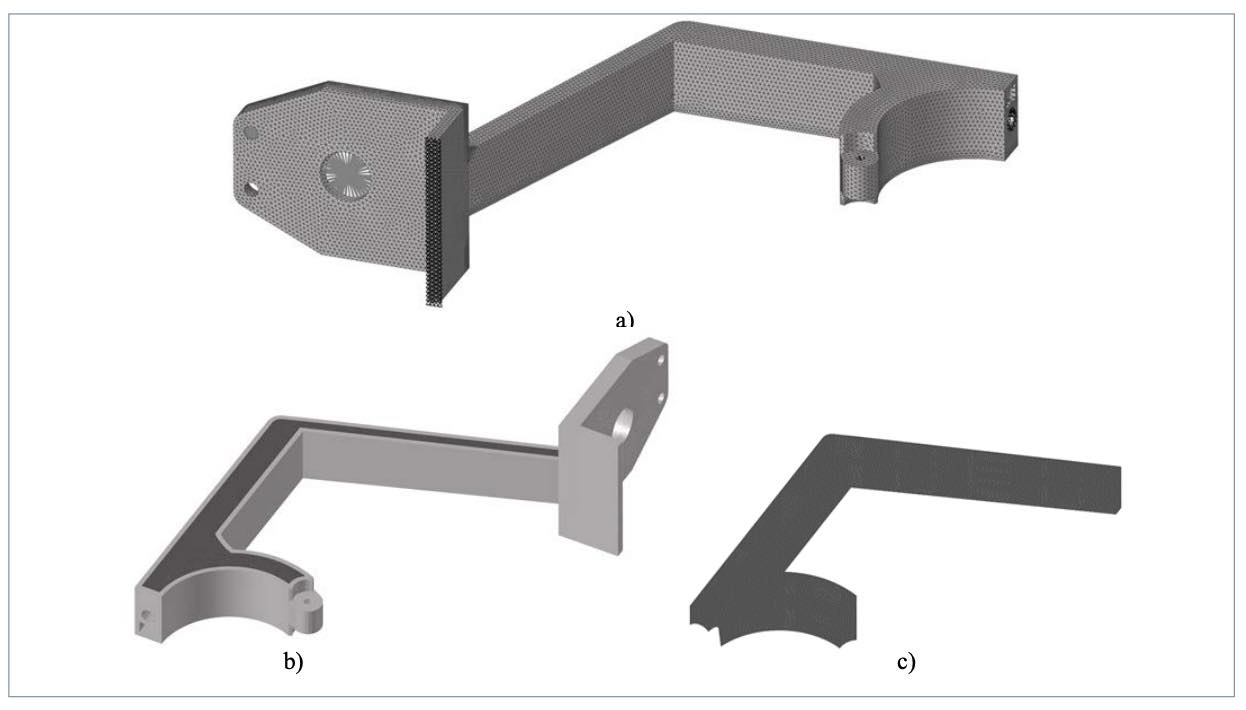
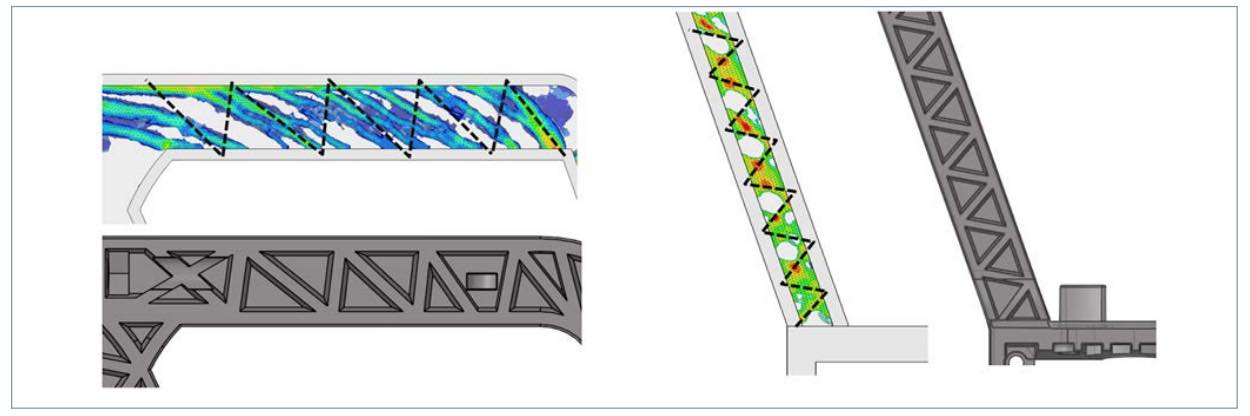
Tras el segundo de optimización, y apoyándose en los patrones de distribución de elementos, se reconstruye la geometría continua según la figura 13. La línea discontinua superpuesta al modelo muestra el patrón seguido para aplicar el nervado.

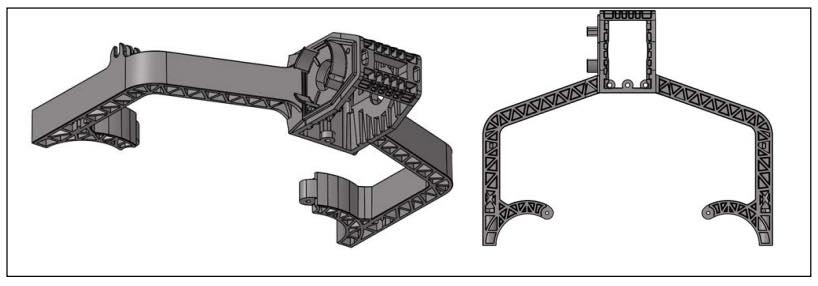
El resultado final de la geometría reconstruida es el mostrado en la figura 14, en la se observa el patrón nervado a lo largo del dominio del componente allí donde se ha definido el espacio de diseño.

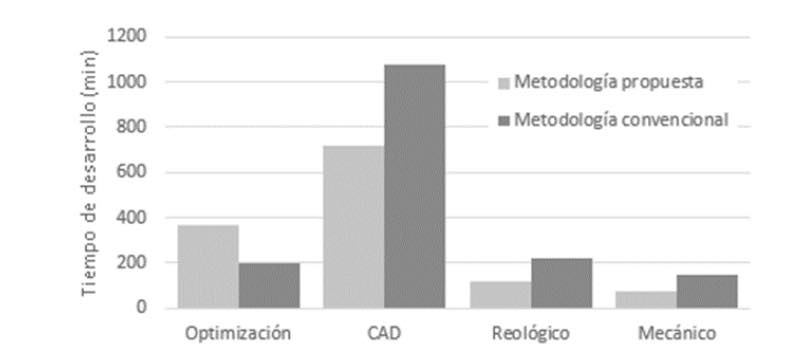
En la figura 15 se muestra un resumen del número del tiempo empleado por cada una de las metodologías, incluyendo el tiempo empleado en la preparación de los modelos. El tiempo computacional se ha tenido en cuenta como tiempo total de procesamiento. En la metodología propuesta, se han requerido dos ciclos de optimización consecutivos, de manera que el diseño, el análisis reológico y la mecánica solo han requerido un ciclo de validación. Por el contrario, la metodología convencional implica solamente un ciclo de optimización, pero requiere dos ciclos tanto en diseño CAD, análisis reológico y análisis mecánico, repetidos en este mismo orden. En total, se ha encontrado una reducción de 1.680 minutos aplicando la metodología convencional a 1.283 minutos mediante la metodología propuesta, lo que supone una reducción del 23,6% en el tiempo total empleado.

 

Conclusiones
Mediante la implementación desarrollada en este trabajo, el cálculo de espesores y análisis de la orientación local aproximada del refuerzo, integrado en el proceso de cálculo, se permite utilizar un modelo no isótropo que reduce el número de ciclos necesarios para alcanzar un modelo mecánicamente válido, además de ofrecer soluciones topológicas más idóneas para el comportamiento ortótropo del material. Es posible aplicar la metodología desarrollada en aquellos componentes fabricados mediante moldeo por inyección y reforzados por fibra corta, dado que los espesores usuales se sitúan en rangos en los que la fibra queda contenida y alineada en planos que pueden ser calculados durante el proceso de optimización.

El hecho de garantizar que la fibra queda contenida y se orienta en un plano permite, en el modelo de Krenchel, el uso de propiedades mecánicas con un factor K = 3/8 en lugar de K = 3/5 correspondiente a fibra aleatoriamente orientada en el espacio. De esta manera, tras varios ciclos consecutivos de optimización se alcanza un modelo discreto válido para las condiciones impuestas, dado que ha tenido en cuenta la propia orientación de la fibra.

Tras realizar el proceso de optimización de una misma geometría y comparar los resultados obtenidos mediante la implementación propuesta y mediante la metodología tradicional, se ha encontrado una reducción total de tiempo del 23,6%, obteniendo geometrías finales muy similares. La aplicación de esta metodología a componentes más complejos podría aportar una mejora notable a los métodos de optimización actualizados actualmente utilizados en el diseño y la manufactura de componentes plásticos reforzados con fibra corta. Su desarrollo e integración en software específico de diseño resultará de interés para el sector.

---

Referencias

[1] Huang, X. and Y. M. Xie. Evolutionary Topology Optimization of Continuum Structures. Methods and applications. UK: John Wiley & Sons, 2010.

[2] Hassani, B. and E. Hinton. Homogenization and Structural Topology Optimization. Theory, Practice and Software. Springer, Berlin, 1999.

[3] Rozvany, G. I. N. and T. Lewinski. Topology Optimization in Structural and Continuum Mechanics. London: Springer, 2014.

[4] Cui, C., H. Ohmori, and M. Sasaki. Computational morphogenesis of 3D structures by extended ESO method. J. Inter. Assoc, vol. 44, pp. 51-61, 2003.

[5] Ohmori, H., H. Futai, T. Iijima, and A. Muto. Application of computational morphogenesis to structural design, in Proceedings of Frontiers of Computational Sciences Symposium, 2005.

[6] Sigmund, O. Tayloring materials with prescribed elastic properties. Mech. Mater., vol. 20, pp. 351-368, 2005.

[7] Torquato, S., S. Hyun, and A. Donev. Multifunctional composites: optimizing microstructures for simultaneous transport of heat and electricity. Phys. Rev. Lett., vol. 89, 2002.

[8] Zhou, S. and Q. Li. Design of graded two-phase microstructures for tailored elasticity gradients. J. Mater. Sci., vol. 43, pp. 5157-5167, 2008.

[9] Bendsøe, M. P. and N. Kikuch .Generating optimal topologies in structural design using a homogenization method. Comput. Methods Appl. Mech. Eng., vol. 71, pp. 197-224, 1998.

[10] Michell, A. G. M. The Limits of Economy of Material in Frame Structures. Philos. Mag., vol. 6-8, pp. 589-597, 1904.

[11] Querin, O. M., M. Victoria, C. Alonso, R. Ansola, and P. Martí. Topology Design Methods for Structural Optimization. London: Elsevier, 2017.

[12] Haftka, R. T. and Z. Gürdal, Elements of Structural Optimization. Kluwer, Dordrecht, 1992.

[13] Bendsøe, M. P. Optimal shape design as a material distribution problem. Struct. Optim., vol. 1, pp. 193-202, 1989.

[14] Bendsøe, M. P. Optimization of Structural Topology, Shape, and Material. Berlin: Springer, 1995.

[15] Bendsøe, M. P. and O. Sigmund. Topology optimisation, Theory, Methods and Applications. Berlin: Springer, 2003.

[16] Rozvany, G. I. N. and M. Zhou. Applications of the COC algorithm in layout optimization, in Engineering Optimization in Design Processes, Berlin: Springer, 1990.

[17] Allaire, G., F. Jouve, and A. M. Toader. Structural optimization using sensitivity analysis and a levelset method. J. Comput. Phys., vol. 194, pp. 363- 393, 2004.

[18] Amstutz, S. and H. Andrä. A new algorithm for topology optimization using a level-set method. J. Comput. Phys., vol. 216, pp. 573-588, 2006.

[19] Wang, M. Y., X. Wang, and D. Uo. A level set method for structural topology optimization. Comput. Methods Appl. Mech. Eng., vol. 192, pp. 227-246, 2003.

[20] Mattheck, C. Engineering components grow like trees. Mater. Sci. Eng. Technol., vol. 21, pp. 143- 168, 1990.

[21] Mattheck, C., M. Scherrer, K. Bethge, and I. Tesari. Shape optimization: an analytical approach. WIT Trans. Built Environ., vol. 80, pp. 137-146, 2005.

[22] Canonaco, M., V. Loher, U., Esslinger, and B. Weisse. Structural optimization methods. WIT Trans. Built Environ., vol. 28, pp. 381-392, 1997.

[23] Xie, Y. M. and G. P. Steven. A simple evolutionary procedure for structural optimization. Comput. Struct., vol. 49, pp. 885-896, 1993.

[24] Xie, Y. M. and G. P. Steven. Evolutionary Structural Optimization. Berlin: Springer, 1997.

[25] Querin, O. M., G. P. Steven, and Y. M. Xie. Evolutionary structural optimization (ESO) using a bidirectional algorithm. Evol. Struct. Optim. using a bidirectional algorithm, vol. 15, pp. 1031-1048, 1998.

[26] SIMULIA. Abaqus Topology Optimization Module. https://www.3ds.com. https:// www.3ds.com/fileadmin/PRODUCTSSERVICES/SIMULIA/RESOURCES/ SIMULIA-Abaqus-Topology-OptimizationModule.pdf (accessed Apr. 15, 2020).

[27] ANSYS. ANSYS Mechanical Topology Optimization. ANSYS Mechanical. .

[28] FEMtools. FEMtools Optimization. Dynamic Design Solutions. https://www.femtools.com/ products/ftopt.htm (accessed Mar. 30, 2020).

[29] Nastran, M. MSC Nastran Topology Optimization product module. MSC Nastran. http://www.mscsoftware.com/assets/3154_ NA2004NOVZTOPZLTDAT.pdf (accessed May 05, 2020).

[30] Altair. Topology Optimization in OptiStruct. HyperWorks OptiStruct. https:// altairuniversity.com/learning-library/ topology-optimization-tutorial-bracket/.

[31] Services, C. E. CATOPO topology optimization toolkit. CATOPO. https://www.catopo.com/ (accessed May 01, 2020).

[32] Compute, D. M. E. and D. Topology Optimization codes. TOPOPT. http://www.topopt.mek.dtu. dk/.

[33] CalculiX. Topology Optimization scripts. CalculiX. http://www.dhondt.de/ccx_2.15.pdf.

[34] CASCADE, O. Topology Optimization codes. SALOME. https://www.salome-platform.org/.

[35] Osswald, T. A. and J. P. Hernández-Ortiz, Polymer Processing: Modeling and Simulation. Munich, 2006.

[36] Tang, S. H., Y. J. Tan, S. M. Sapuan, S. Sulaiman, N. Ismail, and R. Samin. The use of Taguchi method in the design of plastic injection mould for reducing warpage. J. Mater. Process. Technol., vol. 182, pp. 418-426, 2007.

[37] Bozdana, A. T. and Ö. Eyercíoglu. Development of an expert system for the determination of injection moulding parameters of thermoplastic materials: EX-PIMM. J. Mater. Process. Technol., vol. 128, pp. 113-122, 2002.

[38] Khoshooee, N. and P. D. Coates. Application of the Taguchi method for consistent polymer melt production in injection moulding. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf., pp. 611-620, 1998.

[39] Tsoi, H.-P. and F. Gao. Control of injection velocity using a fuzzy logic rule-based controller for thermoplastics injection molding. Polym. Eng. Sci., vol. 39, 1999.

[40] Fadiplast. Inyección y soplado de plásticos. Fadiplast. https://fadiplast.com/ (accessed May 07, 2020).

[41] Reynoso, S. L. Los polímeros plásticos: los conceptos básicos que debes conocer durante y al salir de la Universidad. México: Publicado indepentemente, 2018.

[42] Corporation, B. Bayer Engineering Polymers – Part and Mold Design: Thermoplastics. A Design Guide. 2000.

[43] Jones, R. M. Mechanics Of Composite Materials, 2nd ed. Taylor & Francis, 2015.

[44] Gibson, R. F. Principles of Composite Material Mechanics. CRC Press, 2016.

[45] Papathanasiou, T. D. Flow-induced alignment in injection molding of fiber-reinforced polymer composites, in Woodhead Publishing Series in Composites Science and Engineering, T. D. Papathanasiou and D. C. B. T.-F.-I. A. in C. M. Guell, Eds. Woodhead Publishing, 1997, pp. 112-165.

[46] Vincent, M., T. Giroud, A. Clarke, and C. Eberhardt. Description and modeling of fiber orientation in injection molding of fiber reinforced thermoplastics. Polymer (Guildf)., vol. 46, no. 17, pp. 6719-6725, 2005, doi: https:// doi.org/10.1016/j.polymer.2005.05.026.

[47] Launay, A., M. H. Maitournam, Y. Marco, and I. Raoult. Multiaxial fatigue models for short glass fiber reinforced polyamide – Part I: Nonlinear anisotropic constitutive behavior for cyclic response. Int. J. Fatigue, vol. 47, pp. 382-389, 2013, doi: https://doi.org/10.1016/j. ijfatigue.2012.03.012.

[48] Autodesk. Autodesk Moldflow. Autodesk Moldflow. https://www.autodesk.com/products/ moldflow/overview (accessed May 01, 2020).

[49] Autodesk. Theoretical basis for fiber orientation prediction. Autodesk Moldflow. https://help.autodesk.com/view/MFIA/2019/ ENU/?guid=GUID-50FF496F-0E3E-43CEB30B-4B12CC24F7DE.

[50] Krenchel, H. Fibre reinforcement: theoretical and practical investigations of the elasticity and strength of fibre-reinforced materials. Copenhagen: Akademisk Forlag, 1964.

[51] Blumentritt, B. F., B. T. Cooper, and S. L. Vu. Mechanical properties of discontinuous fiber reinforced thermoplastics. II. Random?in?plane fiber orientation. Polym. Eng. Sci., vol. 15, no. 6, pp. 428-436, 1975, doi: https://doi. org/10.1002/pen.760150606.

[52] Rolland-Nevière, X., D. Gwenaël, and A. Pierre. Robust diameter-based thickness estimation of 3D objects. Graph. Models, vol. 75, no. 6, pp. 279-296, 2013.

[53] Mortazavian, S. and A. Fatemi. Effects of fiber orientation and anisotropy on tensile strength and elastic modulus of short fiber reinforced polymer composites. Compos. Part B Eng., vol. 72, pp. 116-129, 2015