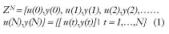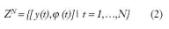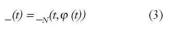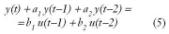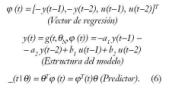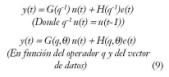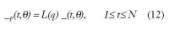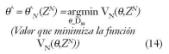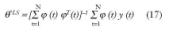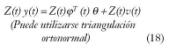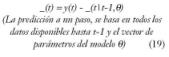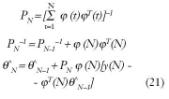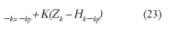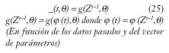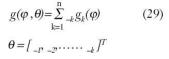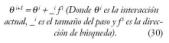Introducción a la identificación de sistemas
Estado del arte de esta técnica para la obtención de modelos matemáticos de sistemas dinámicos a partir de mediciones realizadas en el proceso
El cambio en el proceso productivo, debido fundamentalmente a la evolución de las tecnologías de información y la automatización de los procesos industriales, ha permitido que dichos complejos se adapten al mercado, mejorando sus índices de competitividad, elevando su eficiencia y permitiendo el desarrollo de controladores, que eliminen costos y desperdicios en el proceso de fabricación.
Esto únicamente se puede conseguir con un conocimiento exhaustivo del comportamiento dinámico del proceso, lo que nos permitirá comprender el comportamiento del sistema, incluyendo sus partes críticas.
El modelo del sistema debe entenderse, no sólo en el contexto industrial, se extiende por el resto de sectores y campos del conocimiento como: bioingeniería, economía, termodinámica, organización, construcción…, y su uso va desde el control y la supervisión, hasta la optimización y la predicción, pasando por el diagnóstico y la innovación en sistemas. La mejora continua, y las innovaciones en procesos, hacen necesario el desarrollo de herramientas que ayuden al operador humano en las tareas de supervisión, tareas destinadas a la detección y diagnosis de fallos, comparando el proceso con un modelo de simulación; éstos son los métodos llamados de diagnóstico [Gertler, 98]. Uno de los mayores expertos en este conocimiento, L. Ljung nos dice: “En la actualidad, cada vez más, el trabajo de un ingeniero consiste en la realización de modelos matemáticos”.
Para el diseño de controladores, sean de tipo convencional o avanzado, es necesario disponer de un modelo matemático preciso del proceso a controlar, que nos ayude al diseño de los algoritmos de control. Se incluye una clasificación de los controladores en la tabla 1.
Por consiguiente, tanto para el desarrollo de controladores como para el de métodos de diagnosis y detección de fallos, se hace necesario un profundo conocimiento del sistema o proceso a gobernar, que nos permita conocer el comportamiento del mismo. Esto se conseguirá mediante la utilización de metodologías y protocolos, llamados de identificación de sistemas.
Identificación de sistemas
¿Qué es la identificación?
Podemos definir la identificación de sistemas, como los estudios de técnicas que persiguen la obtención de modelos matemáticos de sistemas dinámicos a partir de mediciones realizadas en el proceso: entradas o variables de control, salidas o variables controladas y perturbaciones (figura 1).
El enfoque de la identificación se puede realizar en función de la estructura del modelo, y del comportamiento físico o no del mismo. Podemos distinguir:
Black-box: los parámetros del modelo no tienen una interpretación física. Un modelo basado en leyes fundamentales es muy complicado o se desconoce.
Gray-box: algunas partes del sistema son modeladas basándose en principios fundamentales, y otras como una caja negra. Algunos de los parámetros del modelo pueden tener una interpretación física; a este tipo de modelos también se les conoce como “Tailor-made”, estimando sólo los parámetros no conocidos.
White-box: la estructura del modelo se obtiene a partir de leyes fundamentales. Los parámetros tienen una interpretación física.
Tipos de modelos
Existen varias formas de catalogar los modelos matemáticos [Ljung, 99]: deterministas o estocásticos, dinámicos o estáticos, de parámetros distribuidos o concentrados, lineales o no lineales, y de tiempo continuo o tiempo discreto; i.e.:
1. Modelos mentales. Sin formalismo matemático.
2. Modelos no paramétricos. Se caracterizan mediante gráficos, diagramas o representaciones que describen las propiedades dinámicas mediante un número no finito de parámetros, i.e., respuesta al impulso, al escalón, o en frecuencia.
3. Modelos paramétricos o matemáticos. Describen las relaciones entre las variables del sistema mediante expresiones matemáticas; i.e., ecuaciones diferenciales en sistemas continuos y ecuaciones de diferencias en sistemas discretos.
En función del tipo de sistema y de la representación matemática utilizada, los sistemas pueden clasificarse en:
– Determinísticos o estocásticos: se dice que un modelo es determinístico, cuando expresa la relación entre entradas y salidas mediante una ecuación exacta; se estudia la relación entre la entrada y la salida con una parte no conocida. Por contra, un modelo es estocástico si posee un cierto grado de incertidumbre. Quedan definidos mediante conceptos probabilísticos o estadísticos.
– Dinámicos o estáticos: un sistema es estático cuando la salida depende únicamente de la entrada en ese instante de tiempo. La función que relaciona las entradas con las salidas, es independiente del tiempo. En un sistema dinámico las salidas varían con el tiempo, el valor actual de la salida en función del tiempo transcurrido desde la aplicación de la entrada. Tienen como objetivo conocer el comportamiento dinámico de un proceso.
– Continuos o discretos: los sistemas continuos trabajan con señales continuas, se formalizan mediante ecuaciones diferenciales. Los sistemas discretos trabajan con señales muestreadas, se describen por medio de ecuaciones en diferencias.
– De parámetros concentrados: no se considera la variación en función del espacio.
– Lineales o no lineales: un sistema lineal se define por una función matemática lineal; i.e., y’(t) + a y(t) = u(t);
siendo y’(t) + a y2(t) + b y3(t) = u(t) no lineal.
Estructura
Para realizar la modelización, es necesario partir de una observación de datos, compuesta de una salida en un instante de tiempo y(t), obtenida a partir de una excitación en el mismo tiempo, u(t).
Por consiguiente, el grupo de observación estará formado por una colección finita de muestras:
Los métodos de identificación tienen, como fin, encontrar un modelo matemático que nos relacione las colecciones de muestras de salidas con las de entrada. Podemos definir el grupo de entrenamiento de forma más general:
Deberemos de estimar y(N+1) a partir de ?(N+1), donde ?(t) es el vector de datos.
Por consiguiente, a partir de aquí lo que buscamos es una función de estimación _N(t,? (t)), que nos permita determinar la salida estimada _(t), tal que:
Donde g será parametrizable, con número finito de parámetros; el vector de parámetros se llamará ?, y la familia de funciones que describen el modelo es la denominada estructura del modelo gN (t,?,?(t)). Entonces la función óptima consistirá en la obtención de un vector de datos ?adecuado, que se realizará en función de los ?^N (estimados).
Para ilustrar lo anterior, si se dispone de un modelo en ecuación de diferencias, tal y como:
Su correspondencia respecto de lo anterior, será:
Métodos de identificación
No paramétricos
La denominada estructura del modelo gN (t,?,?(t)), reduce los modelos parametrizados a una familia de funciones candidatas, pero puede asumirse que una correcta representación del sistema, no puede parametrizarse con un número finito de parámetros; esto se representa por:
Las técnicas de identificación no paramétricas en el caso de sistemas lineales o linealizables, entre otras son:
– Análisis de la respuesta transitoria: consiste en obtener la respuesta del sistema a un impulso o a un escalón.
– Análisis de correlación: pertenece al dominio temporal, se obtiene la función de correlación entre las variables de entrada y salida.
– Análisis en frecuencia: son utilizadas directamente para estimar la respuesta frecuencial del sistema. Se determina mediante el análisis de Fourier o el análisis espectral, dependiendo la forma de las señales de entrada.
Paramétricos
Dado ZN , datos obtenidos por muestreo, en un sistema lineal y estacionario (SLE), entendiendo por:
– Estacionario. Igual respuesta ante una entrada, independientemente del instante de aplicación.
– Lineal. Si la respuesta a una combinación de entradas, es idéntica a la combinación lineal de las respuestas de las entradas.
El modelo de un SLE en tiempo discreto (TD), queda descrito por la respuesta al impulso y calculado como la convolución entre la entrada y la respuesta al impulso del sistema (figura 2).
Por consiguiente, los métodos de estimación paramétrica están muy relacionados con el modelo utilizado y la forma de representar la estructura de un modelo lineal discreto, del tipo anterior. Según [Ljung, 99] es:
Los modelos polinomiales generalizados, polinomizados en q-1 y parametrizados en ?, se expresan de forma general de la siguiente manera y se representan en la figura 3:
Las técnicas de identificación paramétricas se pueden realizar en el dominio temporal, estimación de modelos discretos (Z) o frecuencial, estimación de modelos continuos o discretos (S y Z). Ambas se refieren a la minimización del error:
– Error entre respuesta en frecuencia del sistema y del modelo.
– Error de predicción y error de salida entre el sistema y el modelo.
Principio de identificación
Después de lo comentado anteriormente, el criterio de identificación consiste en evaluar quién de la familia de modelos candidatos se adapta y describe mejor la observación de los datos. Por consiguiente, la esencia del modelo, será su característica de predicción; i.e.: dado un cierto modelo M(?), su error de predicción es:
Según [Ljung, 99], un buen modelo será el que tenga una buena predicción, eso es, aquel que produzca pequeños errores, cuando se le apliquen los datos observados.
El principio será, sobre un Zt computar el error de predicción _(t,?), usando (11), para un t =N, seleccionando un ?^N (estimado), por lo que el error de predicción, _(t,?^N), t =1,2,3…N, llegue a ser lo más pequeño posible.
Si la secuencia (11) se ve como un vector en RN, el tamaño del vector puede ser medido como una norma en RN, cuadrática o no cuadrática, la cual permitirá gran cantidad de elecciones; restringiendo su libertad a la extensión de su secuencia, encontraremos una secuencia filtrada a través de un filtro estable lineal, L(q) (mejor comprendido en el caso de interpretaciones dentro del dominio de la frecuencia).
Usando la norma:
Definiremos la ?^ (estimada) por minimización de (13) como:
Eligiendo como norma cuadrática l(_) =(1/2) _2 la expresión (13) queda:
Derivando la función (16) e igualando a cero, 0 = dd ?VN(?,ZN) , se obtiene:
Ajuste de parámetros
Además del método de mínimos cuadrados y las soluciones al mismo, utilizando la ecuación normal ?^ =(fTf)–1fTY, o la triangulación ortonormal, existe otra serie de métodos para el ajuste de parámetros, detallados a continuación.
– Método de mínimos cuadrados generalizado (GLS), [Åström, 71] y [Zhu, 93]; elimina el inconveniente del método de mínimos cuadrados en lo relativo a la no convergencia de su algoritmo, si la perturbación no es blanca.
– Método de la variable instrumento (IV), consistente en multiplicar la función y(t), por un vector llamado instrumento independiente del ruido, pero muy dependiente del vector de regresión ?(t), quedando:
– Método IV óptimo de Ljung, también denominado óptimo de cuatro etapas, genera el instrumento Z(t) y el filtro, estimando al mismo tiempo tanto la parte determinista, como la estocástica, en cuatro fases.
– Método de la máxima probabilidad (ML); su fundamento es construir una función de probabilidad, para relacionar datos con parámetros desconocidos. La función de probabilidad es una función de densidad de probabilidad y la estimación se resuelve maximizando dicha función (max L(?)=L(?^)).
– Método de predicción de error; consiste en predecir el valor de salida y(t), en función de las entradas y salidas al sistema en los estados anteriores, éste será la diferencia entre la salida estimada y la real.
Formalizando a partir de (9) y asumiendo que tenemos G(0,?) =0, como mínimo un retardo puro entre la entrada y la salida, la forma de expresar el predictor será:
Método recursivo para la estimación de parámetros, los ?^(t) estimados, se calculan a partir de los?^(t-1), utilizando los nuevos u(t),y(t); permitiendo una fácil adaptación a los sistemas variantes en el tiempo, siendo utilizados en control adaptativo y diagnosis.
Partiendo de (17), donde N indica el número de datos, se puede actualizar la estima tras la llegada de un nuevo dato; éste es el llamado método de identificación mediante mínimos cuadrados recursivos (RLS), definimos:
Dando lugar a ?^N = ?^N–1 + K(N)_(N) (Min. Cuadrados recursivos RLS).
Interpretando _(N) como el error de predicción a la salida en N, basándose en la estima del instante anterior y K(N), es la ganancia de la modificación de la estima anterior.
El Filtro Kalman es un algoritmo recursivo, que realiza estimaciones tanto de estados presentes, pasados y futuros, mediante la solución de la estima de mínimos cuadrados.
Utilizando mediciones ruidosas Zk =Hk yk +vk (siendo wk ,vk procesos aleatorios independientes blancos con probabilidad gaussiana).
Fruto de computar la estima a posteriori _k, como una combinación lineal de la estima a priori _kp, de forma factorizada entre la medida real y la predicción de esa medida, se formula de la siguiente manera:
Donde (Zk – Hk _kp), es el residuo o la llamada innovación de la medida, y K es el factor de peso, que minimiza la covarianza del error a posteriori.
Existen otros métodos recursivos como son el método de la variable instrumento recursivo (RIV) y el método de la máxima probabilidad recursiva (RML), derivados de sus correspondientes métodos no recursivos, [Isermann, 91] realizó una comparativa de las propiedades de éstos con el RLS, siendo las principales conclusiones expuestas en la tabla 2.
Sistemas no lineales o no invariantes en el tiempo
El comportamiento y características de los sistemas, en la mayoría de los casos, son no lineales, aunque dentro de una banda de operación los podemos considerar lineales. Por consiguiente, cuando se varía este punto de operación, las características predictivas se ven deterioradas, lo que hace que en la identificación de este tipo de sistema, se recurra a técnicas y modelos no lineales.
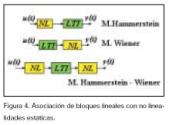
Los sistemas no lineales se pueden representar a través de bloques, modelos orientados a bloques, que representan la conexión de SLE con no linealidades estáticas (saturaciones u otro tipo de no linealidades de elementos del sistema), los modelos más estudiados han sido el modelo Hammerstein y el Wiener, representados en la figura 4.
Los modelos lineales con regresor no lineal quedan definidos:
Donde ?i funciones no lineales de datos pasados, se pueden elegir mediante expansión de tipo caja negra. Los modelos no lineales de este tipo quedan defi-nidos por predictores, con la siguiente forma:
La dificultad reside en elegir el vector de regresión que depende de la aplicación; se eligen típicamente a partir de los modelos lineales y por analogía con éstos, hablamos de estructuras de modelos NARX, NARMAX, NOE, aunque en el caso de modelos de caja negra los más utilizados son NFIR y NARX que sólo dependen de valores medidos y no estimados; i.e.:
De igual forma, existe complicación en cuanto a la elección de la función no lineal g(?,?), para resolver esto, se utiliza expansión en funciones base:
gk(.)(funciones bases). Las funciones bases se eligen a través de series de Volterra o funciones de base madre, clasificadas en bases locales (las variaciones significativas se dan en el entorno) y bases globales (varían de forma significativa en el eje real).
Identificación no lineal a partir de redes neuronales
Las redes neuronales artificiales (ANN) consisten en el procesado sencillo realizado en paralelo por células elementales, llamadas neuronas; éstas están unidas entre sí, formando las capas de la red. La función de la red se debe al tipo de función patrón utilizada, y a las entradas y su factor de peso (figura 5).
Existen tres formas de aprendizaje, de entrenamiento, como son: el supervisado, el de refuerzo y el no supervisado. En síntesis, este aprendizaje consiste en obtener los parámetros que mejor realicen la asociación entre los datos de entrenamiento (entradas y salidas).
Dado el grupo de entrenamiento (1), el objetivo es determinar una estimación de parámetros, desde el grupo hasta los pesos (parámetros): ZN _ ?^; provocando predicciones cercanas a las salidas reales y(t) ˜ _(t).
Para el desarrollo anterior, se sigue como premisa la aproximación a la predicción de error, basada en la introducción de la medida de proximidad en términos del criterio de error de mínimos cuadrados (14) a (17).
Por consiguiente, el esquema de minimización interactiva consistirá en hacer:
Los criterios de entrenamiento se basan en esto; en cómo realizar la forma de búsqueda y cómo seleccionar la dirección y el paso.
La red de Perceptrón Multicapa (o MLP) tiene la capacidad de modelar las relaciones funcionales simples, tan bien como las complejas, y ha sido probada a lo largo de un gran número de aplicaciones prácticas [Demuth & Beale, 1998].
Está formada por dos capas, una oculta y otra de salida, y funciones de activación, lineales o tangentes hiperbólicas (f,F). Los factores (vector ?, o de forma alternativa matrices w y W) son los parámetros ajustables de la red, y están escogidos de un grupo de entrenamiento, que es el grupo de entradas y de salidas u(t) e y(t) a identificar (figura 6).
Proceso de identificación
El proceso de identificación consta de una serie de pautas y decisiones (figura 7), con el objeto de que el modelo final sea representativo del modelo identificado; éstas son:
– Diseño de experimentos: para la obtención de datos de entrada-salida, deberán realizarse experimentos informativos, los datos de un grupo M* de modelos pueden ser discriminados entre dos modelos del grupo; para ello, debe excitarse el sistema con señales lo suficientemente ricas, insistentemente excitadas; u(t) es persistentemente excitada de orden n, si f u(w) (espectro de u(t)), es diferente de cero en al menos n puntos del intervalo -p<?=p.
La elección de las señales se hará teniendo en cuenta:
1. Las propiedades asintóticas de la estima (bias y variance) sólo dependen del espectro de entrada y no de la forma de onda de la señal. Error = bias + variance.
– Bias (desvío): errores sistemáticos causados por características de la señal de entrada, elección de la estructura de modelo (complejidad de la representación) y modo de operación (lazo cerrado o lazo abierto).
– Variance (varianza): errores aleatorios introducidos por la presencia de ruido en los datos, que impiden que el modelo reproduzca exactamente la salida. Está afectado por los siguientes factores: número de parámetros del modelo, duración del experimento de identificación, relación señal-ruido.
2. La entrada debe de estar limitada en amplitud.
3. El orden de la señal, persistentemente excitada, tiene que ser mayor o igual al número de parámetros que van a ser estimados.
4. Las señales periódicas tienen ciertas ventajas.
Tipos de entradas: ruido blanco gaussiano, tiene un valor medio igual a cero y varianza _2; ruido blanco gaussiano filtrado; señal binaria aleatoria, de nivel deseado; señal binaria pseudo aleatoria (PRBS), señal periódica determinista con las propiedades del ruido blanco; señal multisenos, formada por una suma de senoides, persistentemente excitada de orden 2n.
Será necesario tener en cuenta: período de muestreo, número de muestras a tomar, número de registros en PRBS, tiempos de conmutación, amplitud y duración de la señal, bandas de frecuencia…
Observación de datos: será el paso previo antes de realizar la estimación de los parámetros, ya que los datos capturados poseen deficiencias que deberán ser tratadas para una correcta utilización de los modelos citados anteriormente; este tratamiento consistirá: eliminación de pérdida de datos (missing), datos erróneos (outliers), variaciones de tendencia (detrending), estacionalidad (seasonal), impulsos (drifts), señales de offsets, perturbaciones de alta frecuencia, tratamiento de niveles de continua…
Selección de la estructura del modelo: es la fase donde se hace necesario el definir el modelo a emplear: black-box, gray-box, white-box, modelo lineal o no lineal, recursivo o no recursivo, modelos en tiempo continuo o discreto, operación on-line (estimación en tiempo real) u operación off-line (a posteriori), modelos paramétricos, redes neuronales o fuzzy.
Selección del modelo y estimación de parámetros: consistirá en elegir un modelo dentro del grupo que mejor se adapte a los datos, básicamente consistirá en minimizar la función de error de predicción del modelo, y determinar la estimación de los parámetros que minimice el criterio anterior. Técnicas de estimación de parámetros se han citado anteriormente.
Validación del modelo: es la fase donde se comprueba la calidad del modelo, y cómo es capaz de reproducir nuevos grupos de datos; en este sentido, será necesario pro-bar con diferentes órdenes y estructuras en base a unos criterios: a la aplicación del modelo (simulación, predicción, diseño); a la comprobación física de los parámetros, si existe un conocimiento a priori; a la caracterización del comportamiento entrada-salida, comprobando las dinámicas del sistema; a la fiabilidad de los parámetros estimados, conociendo sus índices de desviación estándar; a la comparación de resultados entre el modelo real y el modelo propuesto, y al análisis residual para determinar que el modelo no dependa de los datos ZN, ni de las entradas utilizadas, mediante el análisis de la correlación residual RN_(_) y la covarianza cruzada entre los residuos y las entradas pasadas RN_u(_) (figuras 7 y 8).
Conclusiones
La identificación de sistemas, es una técnica que tiene por objeto, la obtención de modelos matemáticos de sistemas dinámicos, a partir de mediciones realizadas en el proceso; para ello, existe una metodología que consta de una serie de eta-pas, pautas y decisiones, teniendo como fin, que el modelo resultante sea representativo del modelo identificado.
Este procedimiento de identificación, va desde el diseño del experimento, la adquisición y tratamiento de los datos, la elección de la estructura del modelo y la selección de los parámetros, hasta concluir con la fase de validación del modelo. Es necesario apuntar que, para conseguir una coherencia de estimación, todos los pasos citados deben tratarse con el mismo orden y rigor; y descuidos en consideraciones sobre ellos, provocarán inexactitudes y comportamientos erróneos del modelo final.
Bibliografía
Ljung, L. System Identification. Theory for the user. Prentice Hall. 1999.
Söderström, T. y Stoica, P. System Identification. Prentice Hall. 1989.
Ljung, L. System Identification Toolbox: For use with Matlab. The Math Works V 6.0 Noviembre 2003.
Nørgaard, M. Redes neuronales nasadas en el sistema de identificación Toolbox. Informe Técnico 00-E891, Departamento de Automatización Universidad Técnica de Dinamarca, 2000.
Gómez, J.C. Notas de clase. Dpto. de electrónica, FCEIA de la Universidad Nacional de Rosario.
Escobet, T. y Morcego, B. Curso semipresencial de identificación de sistemas de la universidad politécnica de Cataluña.