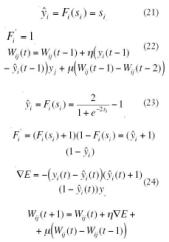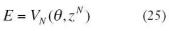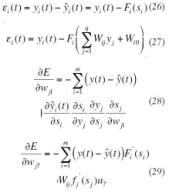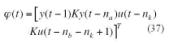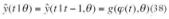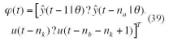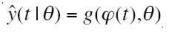Identificación de sistemas no lineales mediante redes neuronales artificiales

Características de las técnicas de identificación neurológica y su aplicación a un modelo construido a partir de un sistema no lineal
Introducción
¿Qué es la identificación?
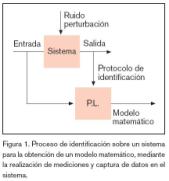
Se puede definir la identificación de sistemas como los estudios de técnicas que persiguen la obtención de modelos matemáticos de sistemas dinámicos a partir de mediciones realizadas en el proceso: entradas o variables de control, salidas o variables controladas y perturbaciones. En la figura 1 se muestra un croquis con estas ideas de forma gráfica.
El enfoque de la identificación se puede realizar en función de la estructura del modelo y de si tienen o no interpretación física sus parámetros. Podemos distinguir las siguientes estructuras: White-box, Gray-box y Black-box20 .
Estructura
Para realizar la modelización, es necesario partir de una observación de datos, compuesta de una salida en un instante de tiempo y(t), obtenida a partir de una excitación en el mismo tiempo u(t).
Por consiguiente, el grupo de observación estará formado por una colección finita de muestras: 
Los métodos de identificación15 tienen como fin encontrar un modelo matemático que nos relacione las colecciones de muestras de salidas con las de entrada. Podemos definir el grupo de entrenamiento de forma más general. 
Se deberá estimar y (t + 1) a partir de d (t + 1), donde d (t) es el vector de datos o vector de regresión. Por consiguiente, a partir de aquí lo que buscamos es una función de estimación g(t, d(t)), que nos permita determinar la salida estimada y(t), predictor tal que:
Donde g será parametrizable, con número finito de parámetros; el vector de parámetros se llamará ? y la familia de funciones que describen el modelo es la denominada estructura del modelo. Entonces la función óptima consistirá en la obtención de un vector de parámetros ? adecuado, que se realizará en función de los ?x(parámetros estimados). 
Sistemas no lineales
El modelo no lineal de ecuaciones diferenciales conocido como modelo Narmax13 es una representación natural del muestreo de sistemas no lineales continuos; proporciona una representación válida para una amplia clase de sistemas lineales y tiene ventajas sobre las series de funciones, tales como las series de Volterra2 .
Desde un punto de vista práctico, existe la necesidad de aproximar el comportamiento de las entradas y salidas a modelos simples y de acuerdo con el teorema de Stone-Weirerstars, los modelos de salida afín y polinómicos son adecuados. Estos modelos son los siguientes:
Modelo general no lineal: Las representaciones de las entradas y salidas que expanden la salida presente en función de sus términos pasados proporcionan modelos que satisfacen una gran clase de sistemas no lineales. El modelo general es el mostrado en la ecuación (5), donde es una función no lineal. Al modelo anterior se le conoce como Armax1, por su semejanza con el modelo lineal representado en la ecuación (6). 
Un sistema invariante en el tiempo y discreto no lineal se puede representar por el modelo (5) en una región próxima al punto de equilibrio, conforme a dos condiciones suficientes [13]: Que la función de respuesta del sistema es finitamente realizable y con la premisa que un modelo linealizado existe, si el sistema trabaja cerca del punto de equilibrio elegido.
Varios modelos no lineales conocidos se pueden identificar con el modelo Narmax, considerándose casos especiales del modelo; a saber, el modelo bilineal, el modelo de salida afín y modelo racional. El modelo bilineal indica que, de forma general, la función causal continua se puede aproximar bien por sistemas bilineales dentro de cualquier intervalo limitado de tiempo [7]. Algunos ejemplos pueden ser las columnas de destilación[5] y los procesos de control termal o nuclear [17]. El modelo general bilineal viene definido por la ecuación (7). 
Los modelos de salida afín y racional surgen a la hora de cumplir las condiciones de la función de respuesta del sistema en lo relativo a la función polinómica y a su límite21. Así, se tendrá que las ecuaciones generales para estos modelos son, bien la ecuación de diferencias racional (8), donde r es el orden del sistema y a(·) y b(·) son los polinomios de grado finito, bien la ecuación de diferencias afín (9), donde los ai(·), con i=0,1,…, r+1, son polinomios de grado finito. 
Identificación no lineal a partir de redes neuronales
Introducción
Las redes neuronales artificiales (ANN) son herramientas de procesado de información, cuyo funcionamiento está basado en operaciones sencillas, realizadas en paralelo por células elementales, llamadas neuronas.
Las ANN son sistemas formados por neuronas, unidas entre sí, formando redes. La neurona, nodo, célula o unidad, será el elemento base del proceso, encontrándose conectada a n entradas, cada una con su factor de peso w; siendo la función de activación de la neurona, la salida y. En la figura 2 se muestra un ejemplo de neurona con las funciones de activación más comunes en identificación de sistemas.
Arquitectura
La arquitectura de una ANN va a depender de: Si las entradas a la neurona son externas o internas, proceden de otras neuronas, U={u0, u1, ······,u N}; de cómo el factor de peso wij se calcula en el proceso de aprendizaje; de la función de activación fi, la cual puede asumir cualquier forma, siendo las de mayor interés, las capaces de discriminar entre rangos de valores; las más usuales son: lineal, simétrica, saturada triangular, logarítmica, tangente hiperbólica, (figura 2); de cómo las neuronas se distribuyen por capas, siendo una capa un conjunto de neuronas semejantes con el mismo comportamiento.
Funcionamiento
Si se parte de una sucesión de datos de entrada u(t) será posible obtener su salida correspondiente y(t) a partir de la función 
(figura 2); si el vector de factores de peso w se encuentra fijo, entonces la red se encuentra en la fase de reconocimiento; por el contrario, si se le permite modificar sus factores de peso, se encuentra en la fase de aprendizaje. En la figura 3 se presenta un ejemplo de una red recursiva de primer orden que se encuentra en la fase de reconocimiento.
Por oro lado, la fase de aprendizaje va a ser el proceso a partir del cual la ANN obtiene los parámetros que mejor se adaptan a la asociación de entradas y salidas. Se puede realizar una clasificación básica de este aprendizaje basándonos en la forma en que se modela el entorno; así se tendrá el aprendizaje:
No supervisado. No disponemos de información de la respuesta prevista, tam-poco se conoce el error cometido.
Por refuerzo. Se dispone de información del error cometido, aunque ésta sea imprecisa.
Supervisado. Se dispone de un grupo de entrenamiento completo, o sea, datos de entrada y datos de salida (1); la salida de la red es la respuesta esperada para esa entrada.
ANN, en los procesos de identificación
Tres preguntas importantes, relativas a las características de la arquitectura más apropiada, surgen cuando se usan ANN en procesos de identificación, las cuales son: número de capas, número de neuronas por capa y funciones de activación.
Muchos autores han investigado al respecto, Kolmogorov, Hecht-Nielsen, Kurkova, Hornik, Cybenko, concluyendo que las ANN de dos capas, con funciones de tipo tangente hiperbólica o sigmoidal en la capa oculta, van a ser predictores universales12 ,3 .
La red de perceptrón multicapa (MLP) tiene la capacidad de modelar las relaciones funcionales simples, también como las complejas. Ha sido probada, a lo largo de un gran número de aplicaciones prácticas, por Demuth & Beale4 .
Está formada por dos capas, una oculta y otra de salida (tres si se considera la capa de entrada, capa transparente), con funciones de activación, lineales o tangentes hiperbólicas (f,F). Los factores (vector ? o de forma alternativa matrices w y W ) son los parámetros ajustables de la red y están escogidos de un grupo de entrenamiento, que es el grupo de entradas y de salidas u(t) e y(t) a identificar. En la figura 4 se muestra una red MLP con una capa de salida y otra capa oculta.
En cambio, no hay trabajos tan concluyentes en lo relativo al número de neuronas por capa, teniendo en cuenta que este número es adecuado para evitar sobreajustes en los datos y evitar que la estructura del modelo elegida contenga demasiados factores de peso. Por consiguiente, se deberán tratar estos posibles excesos a través de una estrategia de reducción OBS (neurocirujano óptimo)9,10.
Otro aspecto importante será conocer cuál de los algoritmos permite un aprendizaje más rápido, para determinar el conjunto óptimo de factores de peso en la ANN. Cada algoritmo se caracteriza por cómo se busca y se selecciona la dirección y el paso; algunos de los algoritmos más usados en la identificación son: método de Lenvenberg-Marquardt[6], método recursivo de predicción de error de Gauss-Newton15 , versión por tandas del algoritmo de retropropagación11 y la versión recursiva de retropropagación11 .
Método de aprendizaje
A partir de la figura 2, se definen todas las variables asociadas a la red; donde:
ui(t)=(u1(t), u2(t), u3(t), K, un(t))
es el vector de entradas del patrón de entrenamiento;
yi(t)=(y1(t), y2(t), y3(t), K, yn(t))
es el vector de salida esperado;
f1(·) ,f2(·), K,fj(·)
son las funciones de activación de las neuronas en la capa oculta;
F1(·) ,F2(·),K , Fi(·)
son las funciones de activación de la capa de salida;
w01, w02, K,wjl
son los pesos de las entradas a la capa oculta, y
w01, w02, K,wij
son los pesos de la capa oculta a la capa de salida.
Las polarizaciones o bias son neuronas unidas al resto con valor 1 y proporcionan niveles de activación independientes de los datos de entrenamiento; sus pesos se modifican de la misma forma que el resto, wj 0y Wj0.
1. Propagación hacia la capa de salida
El vector de entradas u(t) se propaga hacia la capa oculta que cuenta con j neuronas, la excitación de una neurona oculta (sj) quedará definida en la ecuación (10); la salida de la neurona oculta quedará como función del vector de entradas asociado a la función de activación (11). 
Trasladando lo anterior a la excitación de la neurona de salida, ésta queda definida por las ecuaciones (12) y (13). 
Por consiguiente, la formula general de la red MLP puede formarse por la combinación de las ecuaciones anteriores de (10) a (13); como: 
2. Modificación del valor de los pesos de la capa oculta a la capa de salida
La estrategia utilizada es la aplicación del criterio cuadrático medio, mediante la minimización del mismo, por lo que la función de pérdidas o de error dependerá de este criterio, ecuación (14). Entonces el error entre la salida estimada y la salida ideal será ()- yt, que aplicado en cada neurona de la capa de salida dará lugar al error en la neurona, ecuación (15). 
La función de error se minimiza a partir de la elección de la dirección de búsqueda, opuesta a la dirección del gradiente del error E, respecto a los pesos Wij ; por consiguiente, el vector de pesos se modifica en función de una tasa de aprendizaje ? , de la que depende en gran medida la velocidad y tiempo de entrenamiento; a este método se le conoce como de descenso del gradiente, siendo la dirección del gradiente la indicada en la ecuación (16). Se define 
como la sensibilidad de la neurona de salida i ante el vector de entrada y, dado que es posible la utilización de la regla de la cadena, debido a que las funciones de activación son diferenciales, la sensibilidad puede reescribirse en la ecuación (17). 
mediante la ecuación (18), entonces ?E(16) se puede reescribir en la ecuación (19). 
Si el vector de pesos se modifica proporcionalmente en dirección contraria al gradiente y se tiene en cuenta el momento µ, con el fin de reducir el tiempo de aprendizaje y la aparición de mínimos locales, haciendo que la variación de valor de los pesos se realice en la misma dirección, excepto ante cambios de sentido global. La regla de actualización podrá formularse conforme a la ecuación (20), donde. 
Aplicado al cálculo de los pesos de la capa oculta a la capa de salida, en función de la activación de la neurona, se tendrá: funciones de activación lineal, ecuaciones (21) a (22), funciones de tangente hiperbólica, ecuaciones (23) a (24).
3.Modificación del valor de los pesos de la capa de entrada a la capa oculta
La función de pérdidas o de error en m este caso se corresponde con el cálculo a partir de la salida estimada en la capa oculta, la diferencia estriba en que en este caso no se conoce la salida (salida real), pero sí la estimada.
Sustituyendo la sensibilidad de la neurona de la salida i (19), en la ecuación (29); la dirección del gradiente del error respecto a los pesos se reescribe, ecuación(30); siendo la sensibilidad de la neurona j la expresada en la ecuación (31).
Ésta es la esencia del método de entrenamiento de retropropagación, el cual se basa en distribuir los errores que aparecen en las neuronas de salida hacia las neuronas ocultas con las que existe conexión. Por consiguiente, los pesos de las capas de entrada a las capas ocultas se modifican conforme a la siguiente expresión: 
Aplicado al cálculo de los pesos de la capa de entrada a la capa oculta, para unafunción de activación tangente hiperbólica en esta capa, los pesos se modificarán de acuerdo con la ecuación (34). 
Procesos de identificación
Si se parte de una observación objetivo del proceso de identificación consistirá en determinar los factores de peso a ajustar (especificados por w, W o ?), partiendo de la observación ZN.
Entonces el aprendizaje supervisado deberá encontrar el vector de parámetros ?, mediante la aproximación al error de predicción; basándose en la medida de la proximidad, en términos del criterio de error de media de cuadrados, ecuación (14), donde el vector de pesos ? será minimizado VN(,ZN) , ecuación (35). El esquema de minimización iterativa se define en la ecuación (36), donde f(t) es la dirección de búsqueda y µ(t)es el tamaño del paso. 
Selección y estructuras del modelo
Después de realizar la observación ZN, debe elegirse el grupo de regresores y la estructura de red; para la selección de los regresores, como natural extensión de la identificación lineal, nos apoyamos en los modelos lineales [18]. Las estructuras de los modelos se definirán por tres parámetros. p(t): vector de regresión, ? vector de parámetros o pesos y g(·) función de la neurona.
NNARX:
Vector de regresión:
Vector de regresión:
Variante 1
Vector de regresión: 
Donde e(t) es el error de predicción, 
Predictor: 
Variante 2
Vector de regresión:
Predictor: 
NNFIR
Vector de regresión: (42) 
Ensayo. Columna de destilación para la separación de la mezcla de metanol y agua
El proceso de destilación presenta un comportamiento no lineal entre la concentración y el flujo de vuelta, que se produce en la parte superior de la columna; para más detalles ver [8]. Por consiguiente, la ecuación de diferencias de segundo orden, que representa la estructura del modelo, será tomada como si fuera de caja negra y a partir de aquí, excitada con una señal distribuida de forma uniforme con cinco muestras constantes. 
Al sistema se le somete a diferentes tipos de ruidos, con el objeto de ver cómo el entrenamiento de la ANN y el posterior reentrenamiento, una vez que se ha obtenido la estructura óptima de red (OBS), va a ser capaz de predecir la salida.
La estructura de la red vendrá definida: por el número de neuronas en capa oculta (se han utilizado de 10 a 12 neuronas); por el número de parámetros (factores de peso), se han utilizado parámetros arbitrarios de inicio y rearrancado varias veces con el fin de evitar mínimos locales; por la función que debe desarrollar la neurona, tangente hiperbólica en la capa oculta y lineal en la capa de salida; por el orden del modelo y por los algoritmos de búsqueda y dirección, en este caso se ha utilizado el método de Lenverberg-Marquardt, estándar de minimización que utiliza el criterio de error de media cuadrada; en el primer entrenamiento se añade un término de regularización.
La arquitectura óptima se obtiene en base a la regularización, ya que el entrenamiento obedece a criterios que toman mínimos locales y es común que se pueda acabar en un mínimo local no zada sobre los datos de validación no es entrenamiento, pero sin regularización, válido. Por consiguiente, la regularización suaviza los criterios y elimina, en gran medida, los mínimos locales; es decir, se deben eliminar los pesos superfluos y buscar el mínimo error sobre los datos de validación (para la validación de la red).
La estrategia que se ha utilizado después de observar que la validación cruzada no es satisfactoria ha sido utilizar la estrategia OBS, que consiste en encontrar los errores de prueba, estimación más fiable de la generalización del error y seleccionar la ANN con error, sobre la colección de validación, más pequeño.
Por último, una vez que la ANN cuenta con la arquitectura óptima, se ha vuelto a realizar un nuevo ejercicio de entrenamiento, pero sin regularización, recalibrando los parámetros o pesos que definen la ANN. El ensayo se ha realizado usando Matlab con Sys tem Identification Toolbox16 y Neural Network based System Identification Toolbox19. Los resultados gráficos de estos ensayos se muestran en las figuras 5, 6, 7, 8, 9 y 10 y algunos datos significativos se reflejan en la tabla 1.
Resumen
En este artículo se discute la representación de sistemas no lineales en tiempo discreto y el procedimiento de identificación de éstos a partir de estructuras Narmax (Nonlinear Autoregresive Moving Average with eXogenous inputs) mediante la utilización de redes neuronales artificiales ANN. Se van a presentar las características de las ANN, arquitectura, funcionamiento, método de aprendizaje, en los procesos de identificación de sistemas. También se va a construir un modelo basándonos en un sistema no lineal, representado a partir de ecuaciones de diferencias de segundo orden, que representa el comportamiento de una columna de destilación de metanol. Para la identificación del sistema se usará un método no paramétrico, a partir de ANN entrenadas con el método de Levemverg-Marquardt y optimizadas de acuerdo con la estrategia de reducción por neurocirugía OBS.
Conclusiones y trabajos futuros
Se ha mostrado cómo el modelo Narmax es una representación general de los sistemas finitos realizables, donde se incluyen el sistema lineal, el bilineal, el de salida afín y el racional. Se han expuesto las características más importantes de las ANN, cuando participan en procedimientos de identificación. Se ha demostrado cómo se realiza la actualización de los pesos en el proceso de aprendizaje de la ANN. Se ha ilustrado un modelo de la columna de destilación del metanol, que se ha desarrollado usando técnicas de identificación neurológica óptima; red neurológica que se ha entrenado y a la que se le ha aplicado OBS para predecir el comportamiento de la concentración, en función del flujo de vuelta; de igual forma se ha observado la capacidad de predicción del modelo, dependiendo del ruido existente en el sistema.
Nuestro trabajo futuro se desarrollará en la búsqueda de una metodología que conste de una serie de reglas, etapas, pautas y decisiones, capaces de hacer que el modelo final sea representativo del modelo identificado. Este procedimiento de identificación, que irá desde el diseño del experimento, la adquisición y tratamiento de los datos, la elección de la estructura del modelo y la selección de los parámetros, hasta la fase de validación del modelo, deberá tener como aptitudes, la capacidad de poderse ejecutar de forma automática.
Referencias
- S. A. Billings e I. J. Leontaritis, “Parameter estimation techniques for nonlinear systems”, Proc. 6th IFAC Symposium on Identification and System Parameter Estimation, Washintong, USA, 1982. pp. 505-510.
- S. Chen y S. A. Billings, “Representations of nonlinear systems: The Narmax model”, Taylor & Francis Ltd. Int. J. Control, Vol. 49, N.º 3, 1989. pp. 1013-1032.
- G. Cybenko, “Aproximation by superpositions of sigmoidal function”, Math. Control, Sygnals and System, vol. 2, n.º 4, 1989
- H. Demuth & M. Beale “Neural Network Toolbox: For use with Matlab”. The MathWorks Inc., Natick, MA, 2005.
- M. España e I. D. Landau, Automatica, Vol. 14, 345, 1978.
- R. Fletcher “Practical Methods of Optimization”, Wiley, 1987.
- M. Fliess, y D. Normand-Cyrot, “On the approximation of nonlinear systems by some simple state-space models”, Proc. 6th IFAC Symposium on Identification and System Parameter Estimation, Washintong, USA, 1982. pp. 511-514.
- R. Haber and L. Keviczky. “Nonlinear System Identification-Input-output Modelling pproach”, Vol 2, Kluwer Academic Publishers 1999.
- L. K. Hansen & M. W. Pedersen “Controlled Growth of Cascade Correlation Nets”, Proc. ICANN 94, Sorrento, Italia, Eds. M. Marinaro & P. G. Morasso, pp. 797-800, 1994.
- B. Hassibi, D. G. Stork “Second Order Derivatives for Network Pruning: Optimal Brain Surgeon”, NIPS 5, Eds. S. J. Hanson et al., 164, San Mateo, Morgan Kaufmann, 1993.
- J. Hertz, A. Krogh & R. G. Palmer “Introduction to the Theory of Neural Computation”, Addison-Wesley, 1991.
- Hornik, K., Stinchcombe, M. and White H. “ Multilayer Feedforward Networks are Universal Aproximators”, Neural Networks, vol. 2 n.º 5, 1989.
- I. J. Leontaritis, y S. A. Billings, Int. J. Control, Vol. 41, 303, 1985.
- J. Larsen & L. K. Hansen “Generalization Performance of Regularized Neural Network Models”, Proc. of the IEEE Workshop on Neural networks for Signal Proc. IV, Piscataway, New Jersey, pp. 42-51, 1994.
- L. Ljung. “System Identification. Theory for the user”. Prentice Hall. 1999.
- L. Ljung. “System Identification Toolbox: For use with Matlab”. The MathWorks 2005.
- R. R. Mohler, “Bilinear Control Processes”, Academic Press, 1973.
- M. Nørgaard, O. Ravn, N. K. Poulsen, L. K. Hansen “Neural networks for Modelling and Control of Dynamic Systems”, Springer-Verlag, Londres, UK, 2000.
- M. Nørgaard. “Neural network Based System Identification Toolbox” Report Technical Tecnico 00E-891, Department de Automation Technical University de Dinamarca, 2000.
- J. Sedano, J. R. Villar “Aproximación a la teoría de la indentificación de sistemas, “system identification“, estado del arte “ , Técnica Industrial 1/05, pp. 30-36, 2005
- E. D. Sontag, “Polynomial response maps”, Lecture Notes in Control and Information Sciences 13, Springer-Verlag, 1979.