Estimación de prestaciones en una motocicleta de competición
Performance estimation of a racing motorcycle
A. Noriega González 1, I. Fernández de Bustos 2
Resumen
La competición Motostudent implica el diseño, construcción y puesta a punto de una motocicleta de competición que debe pasar una serie de pruebas dinámicas durante la fase final de dicha competición. Entre esas pruebas se incluyen una prueba de aceleración, una prueba de frenada, la obtención de la velocidad máxima en el circuito y la mejor vuelta realizada al mismo. Dado que las pruebas comentadas son puntuables, resulta de gran interés disponer de una herramienta de simulación que permita estimar el rendimiento alcanzable por un diseño de motocicleta o una puesta a punto de la misma en función de ciertos parámetros ajustables como puede ser la curva de par del motor, el desarrollo de la transmisión, la posición del centro de masas, etc. Esta herramienta debe ser paramétrica, robusta y muy eficiente para poder automatizar más adelante el proceso de obtención de los parámetros óptimos para el diseño o la puesta a punto. En este artículo se muestra cómo se ha realizado el modelado de la dinámica longitudinal de una motocicleta de competición de la categoría Motostudent Petrol, despreciando los efectos de cabeceo e inclinación lateral. El modelo de piloto gestiona el cambio de marchas, el control de tracción y anticaballito, así como la elección del punto de frenada óptimo. Basándose en este modelado, se realiza una simulación dinámica que permite calcular, de manera detallada, el movimiento de la moto a lo largo de una recta y estimar las prestaciones anteriormente comentadas asociadas al diseño o puesta a punto que se desee estudiar. La herramienta desarrollada se ha validado comparando las prestaciones calculadas con las obtenidas por motocicletas participantes en ediciones pasadas de la competición Motostudent Petrol.
Palabras clave: Simulación, prestaciones, motocicleta, competición.
Abstract
The Motostudent competition involves the design, construction and tuning of a racing motorcycle that must pass a number of dynamic tests during the final phase of the competition. These tests include an acceleration test, a braking test, obtaining the maximum speed on the circuit and the best lap of the circuit. Since the tests mentioned above are scoring tests, it is of great interest to have a simulation tool that allows estimating the achievable performance of a motorcycle design or tuning depending on certain adjustable parameters such as engine torque curve, transmission ratio, center of masses position, etc. This tool must be parametric, robust and highly efficient in order to automate later the process of obtaining the optimal parameters for the design or tuning. This paper shows how the longitudinal dynamics of a Motostudent Petrol racing motorcycle has been modeled neglecting the effects of pitch and lateral tilt. The rider model manages the gear shifting, traction control and antiwheelie, as well as the choice of the optimal braking point. Based on this modeling, a dynamic simulation is performed to calculate, in detail, the movement of the motorcycle along a straight line and to estimate the abovementioned performance associated with the design or tuning to be studied. The developed tool has been validated by comparing the calculated performance with those obtained by motorcycles participating in past editions of the Motostudent Petrol competition.
Keywords: Simulation, performance, motorcycle, racing.
Recibido/received: 01/06/2023 Aceptado/accepted: 10/10/2023
1 Departamento de Construcción e Ingeniería de Fabricación, Universidad de Oviedo.
2 Departamento de Ingeniería Mecánica, Universidad del País Vasco.
Autor para correspondencia: Álvaro Noriega González; e-mail: noriegaalvaro@uniovi.es
1. Introducción
La competición Motostudent es un desafío bienal entre universidades de todo el mundo en el que un equipo de estudiantes universitarios debe diseñar una motocicleta de competición de pequeño tamaño bajo unos condicionantes técnicos comunes, así como realizar y defender ese diseño y el plan de negocio asociado ante un tribunal de especialistas del sector. Además, cada equipo universitario debe construir la motocicleta diseñada, la cual debe pasar una serie de pruebas estáticas y dinámicas para comprobar el cumplimiento de la reglamentación y la seguridad del vehículo. Finalmente, si el prototipo construido se considera apto, pasa a disputar una carrera, incluida en el calendario de la Federación Internacional de Motociclismo (FIM), y que se disputa en el circuito de velocidad de Motorland Aragón, en España (Gadola, 2019).
En la competición Motostudent hay dos categorías. En la categoría Petrol, todas las motos llevan un motor de combustión interna de cuatro tiempos y 250 cc y en la categoría Electric, un motor eléctrico. En ambos casos, la organización proporciona los motores a utilizar y estos se encuentran precintados para evitar que se puedan manipular. Aparte del motor, la organización también proporciona los neumáticos y las pinzas y mandos de los frenos. Y a partir de ahí, los equipos tienen mucha flexibilidad para diseñar su motocicleta, respetando una normativa básica centrada principalmente en la seguridad. Esta flexibilidad permite innovar, pero también genera muchas dudas al inicio del proceso de diseño, sobre todo entre los participantes, que son estudiantes con muy poco bagaje práctico en el diseño de vehículos.
Los autores de este artículo llevan participando en esta competición desde sus inicios, tutorizando equipos en sus respectivas universidades y han observado que, durante la toma de decisiones sobre la geometría básica de la motocicleta, la cual va a determinar sus prestaciones, los estudiantes desearían estimar las prestaciones que serían alcanzables por diferentes diseños para poder decidir cuál sería el diseño óptimo. Esto puede hacerse, en un inicio, tomando como referencia los diseños de motocicletas de competición similares a la que se desea construir (se trataría de un diseño por analogía), pero esto no permite la comprensión completa de las razones que están detrás de dicho diseño. Por esta razón, les resultaría de gran utilidad una herramienta que, utilizando unos pocos parámetros de diseño, pueda estimar, de manera aproximada, las prestaciones de la motocicleta en las pruebas dinámicas que son puntuables para la competición. Es cierto que hay modelados más complejos, que incorporan muchos datos y detalles, como el de Lesina (2022), los cuales permiten obtener resultados más precisos, pero dichos modelos no son adecuados para una etapa inicial de un nuevo diseño, precisamente por el nivel de detalle que exigen en el modelo a simular en un momento en el que dicho diseño está relativamente indefinido.
Otra observación basada en la experiencia es que, una vez construido el prototipo, se dispone de escaso tiempo para pruebas en pista previas a la competición. Además, en muchos casos, la localización alejada de circuitos adecuados para realizar estas pruebas, la disponibilidad de pilotos para realizarlas, los medios disponibles (como adquisición de datos y transporte) y el coste económico asociado (desplazamiento y alojamiento) hace que estas pruebas previas sean escasas o directamente inexistentes. Sin ellas, resulta muy complicado ajustar de manera óptima ciertos parámetros, como el desarrollo para la transmisión por cadena o la curva de par del motor, que deben dejarse, entonces, para la competición final, en la que únicamente se dispone de dos sesiones de entrenamientos libres para ajustar los parámetros indicados junto con otros como el reglaje de las suspensiones. Si se dispusiera de una herramienta que permitiera simular de manera sencilla, pero con cierta fiabilidad, el comportamiento de la motocicleta en las distintas pruebas a realizar en el circuito o en partes de ellas, se facilitaría la decisión del diseño o compra de componentes como los elementos de la transmisión y el ajuste de la curva de par del motor sin necesidad de realizar pruebas intensivas en circuito, o al menos, reduciéndolas significativamente.
Las pruebas dinámicas que son puntuables en la competición Motostudent son las siguientes:
•Test de frenado.
•Yincana.
•Test de aceleración.
•Posición en la parrilla de salida.
•Mejor vuelta rápida.
•Velocidad máxima en pista.
•Posición final en la carrera.
Varias de estas pruebas (el test de frenado, el test de aceleración y la velocidad máxima en pista, la cual siempre se alcanza en la recta de atrás del circuito de Motorland Aragón) se desarrollan con la motocicleta circulando en línea recta y en una superficie sin peralte lateral, por lo que puede tener pendiente longitudinal positiva o negativa. En esta situación, el modelo de piloto se simplifica en gran medida, dado que solo debe controlar la aceleración y el frenado longitudinal, asegurando que los neumáticos trabajen al límite de su adherencia y que la motocicleta no sufra el despegue de sus ruedas respecto del suelo. También debe manejar el embrague y el cambio de marchas, en el caso de que la motocicleta disponga de ellos (obligatorio en la categoría Petrol y opcional en la categoría Electric).
Estas pruebas, que se realizan en línea recta, y otras similares a distinta velocidad, pueden simularse de manera sencilla en un ordenador y también realizarse en entornos controlados con el prototipo real una vez construido, comparando los resultados de ambas para valorar la precisión del modelo y la simulación realizados e identificar los parámetros sobre los que hay más incertidumbre. Esto permite ir ajustando de manera iterativa el modelo de simulación con los datos reales obtenidos y validar esta herramienta para ser usada en futuros diseños.
Para dar respuesta a esta necesidad, en este artículo se describirá cómo se puede realizar un modelado y una simulación simplificados, pero funcionales para una motocicleta de la categoría Petrol realizando pruebas, o partes de pruebas, que se desarrollen en línea recta y la validación de los resultados obtenidos de la simulación comparándolos con los resultados medidos en el desarrollo de esas pruebas en la realidad.
2. Datos conocidos de la motocicleta
Para desarrollar un modelo simplificado de la dinámica longitudinal de la moto en un tramo recto y sin peralte lateral, se puede considerar lo siguiente:
El movimiento de la motocicleta se considera contenido en un plano vertical, con sus neumáticos apoyando en su parte central.
•No se considerará el cabeceo, ni el efecto de las suspensiones, ni la flexibilidad de los neumáticos ni el movimiento del piloto encima de la moto, por lo que puede considerarse que el movimiento de la motocicleta tiene un solo grado de libertad (en la dirección de avance de la motocicleta).
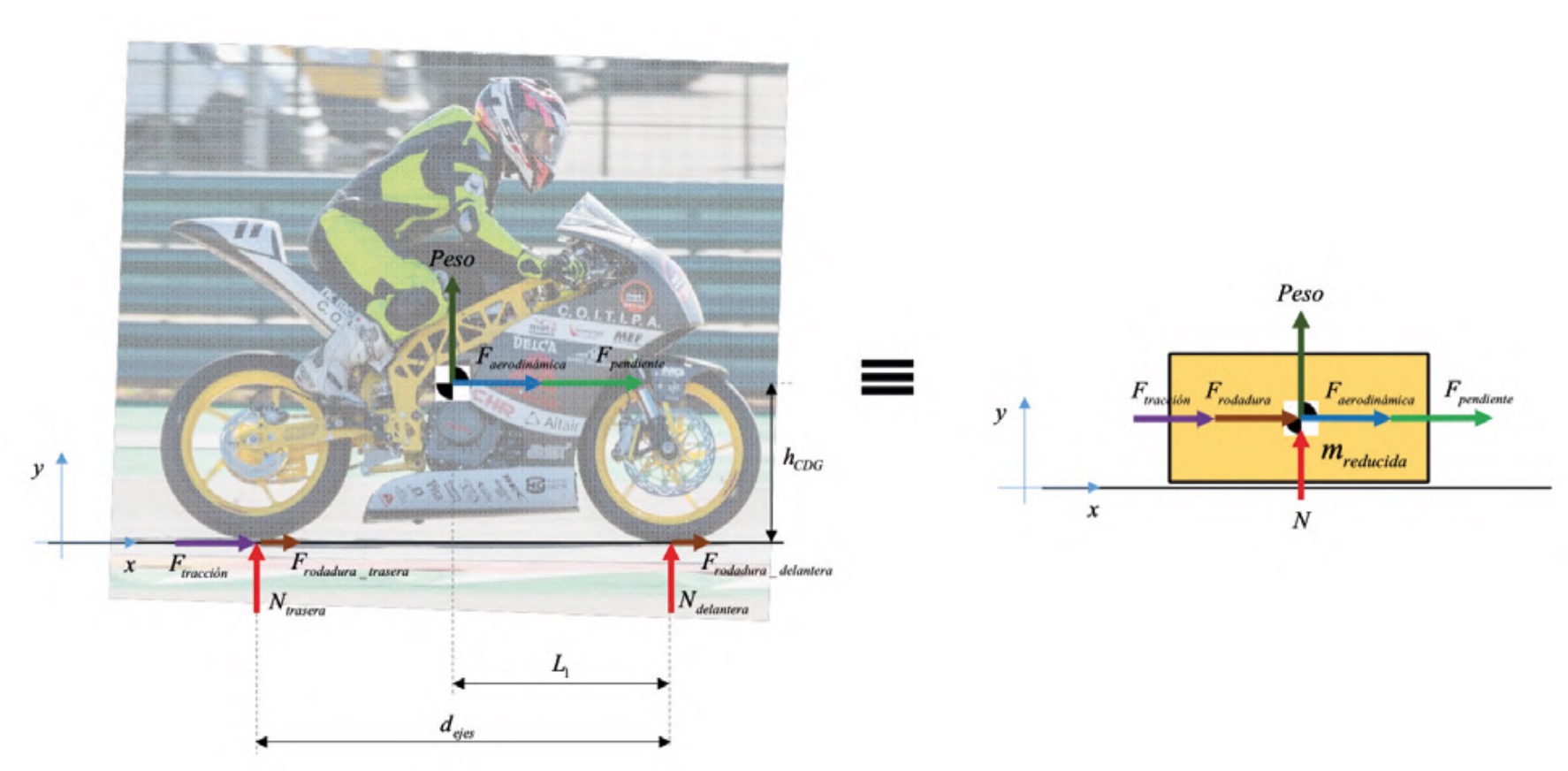
•Se obtendrá un modelo de la dinámica reducido a un grado de libertad, similar al propuesto en Hauser (2006), como se indica en la figura 1.
•Las direcciones y los sentidos de las fuerzas aplicadas sobre la motocicleta (v. fig. 1) son los habituales en simulación multicuerpo, coincidiendo el sentido positivo de velocidades, aceleraciones y fuerzas, para ser coherente con la segunda ley de Newton. Tanto los componentes de las fuerzas como los de las aceleraciones se esquematizan siempre en el sentido positivo de los ejes del sistema de referencia, dado que algunos de ellos pueden cambiar de sentido durante la simulación. Si se conoce el sentido de alguna de las fuerzas actuantes, se introducirá el signo en la ecuación correspondiente, como se puede ver en las expresiones (4). Este tipo de esquematización permite una formulación más sencilla y directa de las ecuaciones de la dinámica.
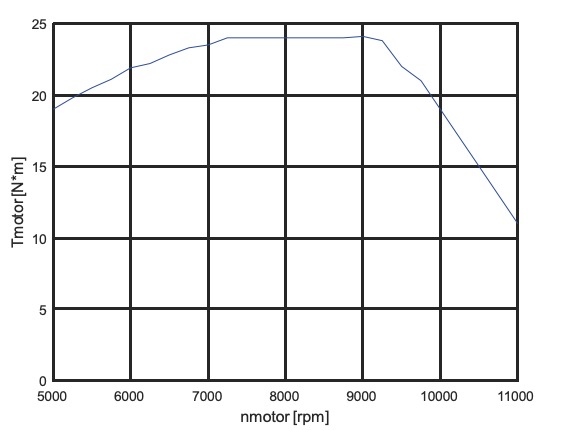
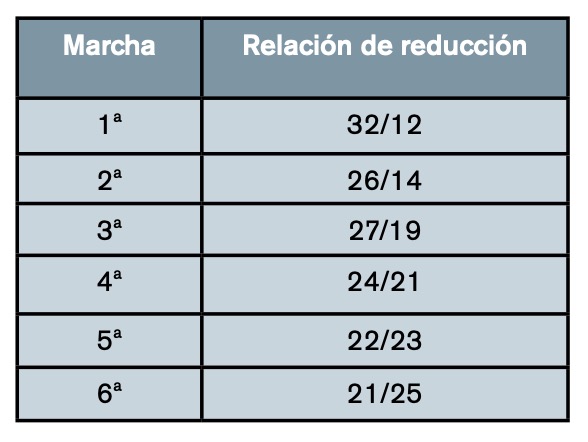
Teniendo en cuenta lo anterior, se necesitarán los siguientes datos de la motocicleta: Motor de combustión interna y caja de cambios asociada: se conocerá el momento de inercia del conjunto reducido a su cigüeñal, la curva de par motor al cigüeñal (de donde se obtendrá su par máximo Tmáx y su velocidad de rotación mínima nmín y máxima nmáx operativas). En el caso de las ediciones V y VI de la competición Motostudent, se utilizó un motor de origen KTM con la curva de par que se puede ver en la figura 2. La caja de cambios tiene una relación de reducción primariaIprimario de 80/30 y seis marchas con las relaciones de reducción indicadas en la tabla 1. Tiene un rendimiento mecánico ?cc de 0,95. La caja de cambios incorpora un quickshifter que realiza el cambio de marcha en 0,12 s. Transmisión secundaria: por cadena, de la que se conocerá la relación de reducción icadena (37/14, modificable) y su rendimiento mecánico ?cadena de 0,95. Resistencias al avance: se considera conocida la resistencia a la rodadura de los neumáticos frodadura (0,02, igual para el delantero y el trasero y relaciona la carga vertical que recibe el neumático con la fuerza tangencial que se opone al avance del mismo mientras rueda), el coeficiente de penetración Cx de 0,45, la superficie frontal S de 0,4 m2 y la densidad de aire ?aire de 1,29 kg/m3 .
Dimensiones: se considerará conocida la distancia entre ejes dejes de 1.300 mm, la distancia entre el CDG y el primer eje l1 de 650 mm y la altura del CDG hCDG de 645 mm (v. fig. 2). La posición del CDG tiene en cuenta la masa conjunta de motocicleta y piloto. Pesos: se considerará conocida la masa de la motocicleta en estado de marcha mmoto de 110 kg y la masa del piloto completamente equipado mpiloto de 85 kg. Ruedas y neumáticos: se considerará conocido el momento de inercia de ambas ruedas respecto a sus ejes, el radio efectivo del neumático trasero rtras de 0,30065 m y un coeficiente de adherencia longitudinal ? de 1,3 el cual se considera constante e igual para los neumáticos delantero y trasero. Los datos mostrados pertenecen al prototipo desarrollado por el equipo Bizkaia ESI Bilbao.
3. Modelado de la dinámica en una recta
Para modelar el comportamiento de una motocicleta de competición en velocidad, hay que considerar que el fin último de la misma es recorrer la recta en el menor tiempo posible (Cossalter, 1998). A partir de esto, no habrá tramos de velocidad constante (salvo cuando el motor llegue a su límite máximo de velocidad de rotación). Entonces, la recta puede dividirse en dos sectores consecutivos y claramente diferenciados: la zona de aceleración y la zona de frenada. El modelo dinámico en esos dos sectores es diferente (la tracción está solo en la rueda trasera, pero el frenado se realiza con las dos ruedas) y también el modelo de piloto, que actúa de manera diferente, en un caso acelerando y subiendo marchas y, en el otro caso, frenando y bajando marchas.
El problema de simulación tendrá, además, unas condiciones de contorno diferentes a las clásicas en simulación (un problema de valores iniciales) ya que se conocerá la velocidad vini y la marcha nccini en la que inicia la recta, la longitud l y la pendiente ? de la recta y también se conocerán la velocidad vfin y la marcha nccfin al final de la recta. El punto de frenado xfrenado está situado dentro de la recta y marca el cambio de la dinámica y el modelo de piloto que se aplica. Ese punto de frenado está situado de tal manera que la velocidad y la marcha engranada al final de la recta sean las establecidas en las condiciones de contorno de la simulación. Este punto de frenado habrá que obtenerlo resolviendo un problema de optimización.
La simulación de la dinámica tanto en la zona de aceleración como en la de frenada se realizará utilizando un integrador numérico sencillo modificado para incluir un criterio de parada que asegure que se recorre toda la recta, es decir, asegurando la robustez de la metodología.
A continuación, se pasa a describir el detalle de las situaciones y formas de actuar comentadas:
3.1. Zona de aceleración
En la zona de aceleración, el modelo dinámico a considerar es el indicado en la figura 1 y sobre el mismo se plantea la ecuación diferencial del movimiento de Eksergian (1930) mostrada en (1).
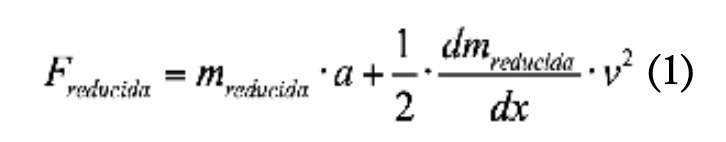 La masa reducida se calcula igualando energías cinéticas del sistema original (motocicleta con piloto) y el sistema reducido, que es una masa puntual equivalente situada en la posición del CDG del sistema original. Desarrollando esa igualdad y teniendo en cuenta la inercia de las masas rotantes en la motocicleta, se puede llegar a la expresión (2).
La masa reducida se calcula igualando energías cinéticas del sistema original (motocicleta con piloto) y el sistema reducido, que es una masa puntual equivalente situada en la posición del CDG del sistema original. Desarrollando esa igualdad y teniendo en cuenta la inercia de las masas rotantes en la motocicleta, se puede llegar a la expresión (2).
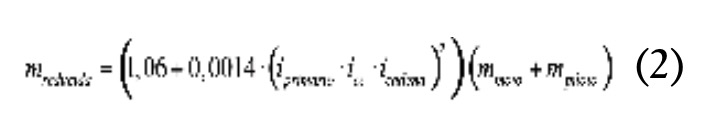 Para calcular la fuerza reducida, se tendrán en cuenta todas las resistencias al avance y la fuerza de tracción generada en la rueda trasera, llegando a la expresión (3). Donde:
Para calcular la fuerza reducida, se tendrán en cuenta todas las resistencias al avance y la fuerza de tracción generada en la rueda trasera, llegando a la expresión (3). Donde:
 Sustituyendo en la expresión (1), se puede llegar a la expresión (5).
Sustituyendo en la expresión (1), se puede llegar a la expresión (5).
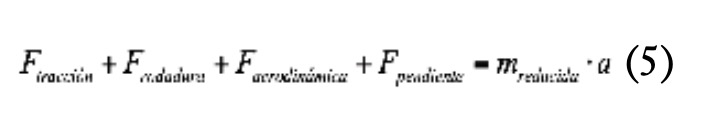 La expresión (5) debe integrarse respecto al tiempo, para lo que se consideran conocidas, en cada instante, la posición x y la velocidad v y se calculará la aceleración a. Para ello, a partir de la velocidad de la motocicleta, puede calcularse la velocidad de rotación del motor con la expresión (6).
La expresión (5) debe integrarse respecto al tiempo, para lo que se consideran conocidas, en cada instante, la posición x y la velocidad v y se calculará la aceleración a. Para ello, a partir de la velocidad de la motocicleta, puede calcularse la velocidad de rotación del motor con la expresión (6).
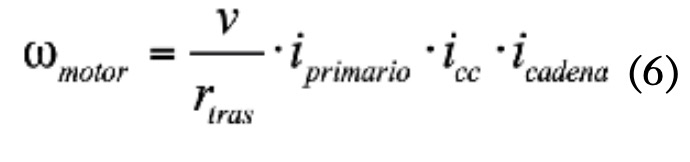 La elección de la marcha a utilizar en cada momento se realiza mediante la utilización de un algoritmo de cambio de marcha que tiene en cuenta:
La elección de la marcha a utilizar en cada momento se realiza mediante la utilización de un algoritmo de cambio de marcha que tiene en cuenta:
•El instante de simulación.
•La velocidad de rotación de la rueda.
•La marcha engranada.
•El instante en el que realizó el último cambio de marcha.
•La posición de la moto en la recta (si está acelerando o frenando).
•La marcha más alta que puede utilizar en el tramo de recta.
•La curva de par motor. Y proporciona:
•La velocidad de rotación del motor.
•La marcha engranada óptima para maximizar la fuerza de tracción si está acelerando y para mantener el motor por encima del régimen de par máximo si está frenando.
•El instante actualizado en el que se realizó el último cambio de marcha.
Conocida la velocidad del motor, se puede calcular el par generado por el mismo interpolando en la curva de par motor que puede verse en la figura 2. Cuando la velocidad de giro del motor está por debajo de la velocidad mínima operativa en competición, se entiende que el piloto pellizca el embrague (maniobra que consiste en desconectar la transmisión, acelerar el motor y volver a conectar la transmisión) generando una situación transitoria que se traduce un incremento de par súbito y momentáneo percibido en la transmisión. En esta situación, se ha decidido aplicar un par 1,5 veces mayor que el par máximo, ya que se ha comprobado que con ese par, se produciría una situación de levantamiento de la rueda delantera durante un arranque en parado, que es lo ocurre en la realidad en muchas ocasiones durante el test de aceleración.
A continuación, se puede calcular el par que suministraría el motor a la rueda con la expresión (7), la fuerza de tracción que se generaría, suponiendo una situación de no deslizamiento del neumático, con la expresión (8) y la máxima aceleración que permitiría el motor con la expresión (9).
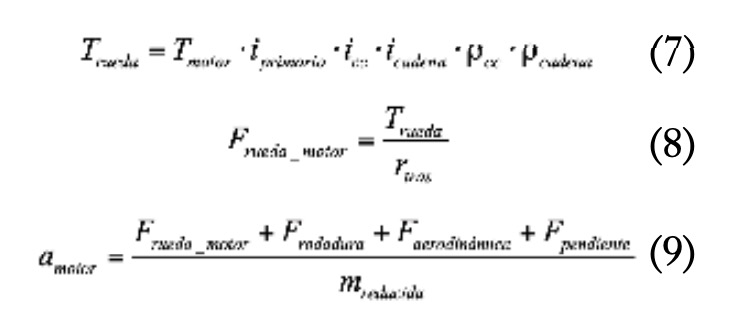 En paralelo, se puede calcular la máxima fuerza de tracción que se conseguiría llevando al límite la adherencia del neumático trasero (Luque, 2004) con la expresión (10) y la máxima aceleración que permitiría la adherencia con la expresión (11).
En paralelo, se puede calcular la máxima fuerza de tracción que se conseguiría llevando al límite la adherencia del neumático trasero (Luque, 2004) con la expresión (10) y la máxima aceleración que permitiría la adherencia con la expresión (11).
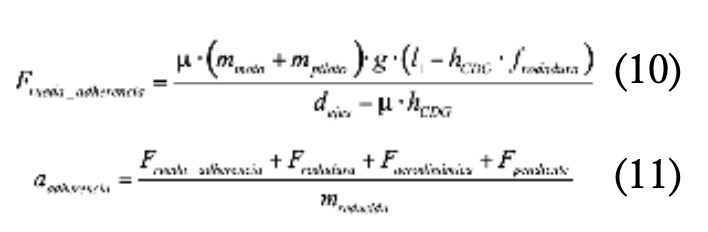 Finalmente, se puede calcular la aceleración que generaría un despegue de la rueda delantera con la expresión (12).
Finalmente, se puede calcular la aceleración que generaría un despegue de la rueda delantera con la expresión (12).
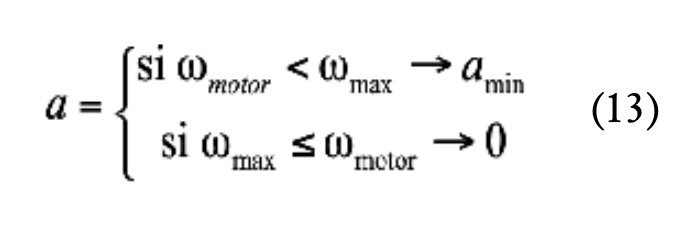
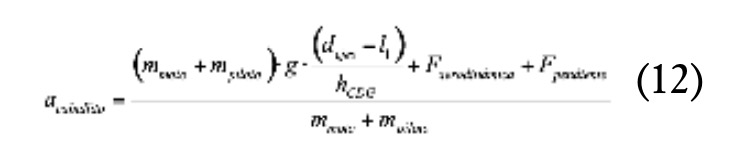 De las tres aceleraciones calculadas, se escogerá la mínima aceleración de las tres amin y se implementará un límite adicional cuando el motor haya alcanzado su máxima velocidad operativa con la expresión (13).
De las tres aceleraciones calculadas, se escogerá la mínima aceleración de las tres amin y se implementará un límite adicional cuando el motor haya alcanzado su máxima velocidad operativa con la expresión (13).
 3.2. Zona de frenada
3.2. Zona de frenada
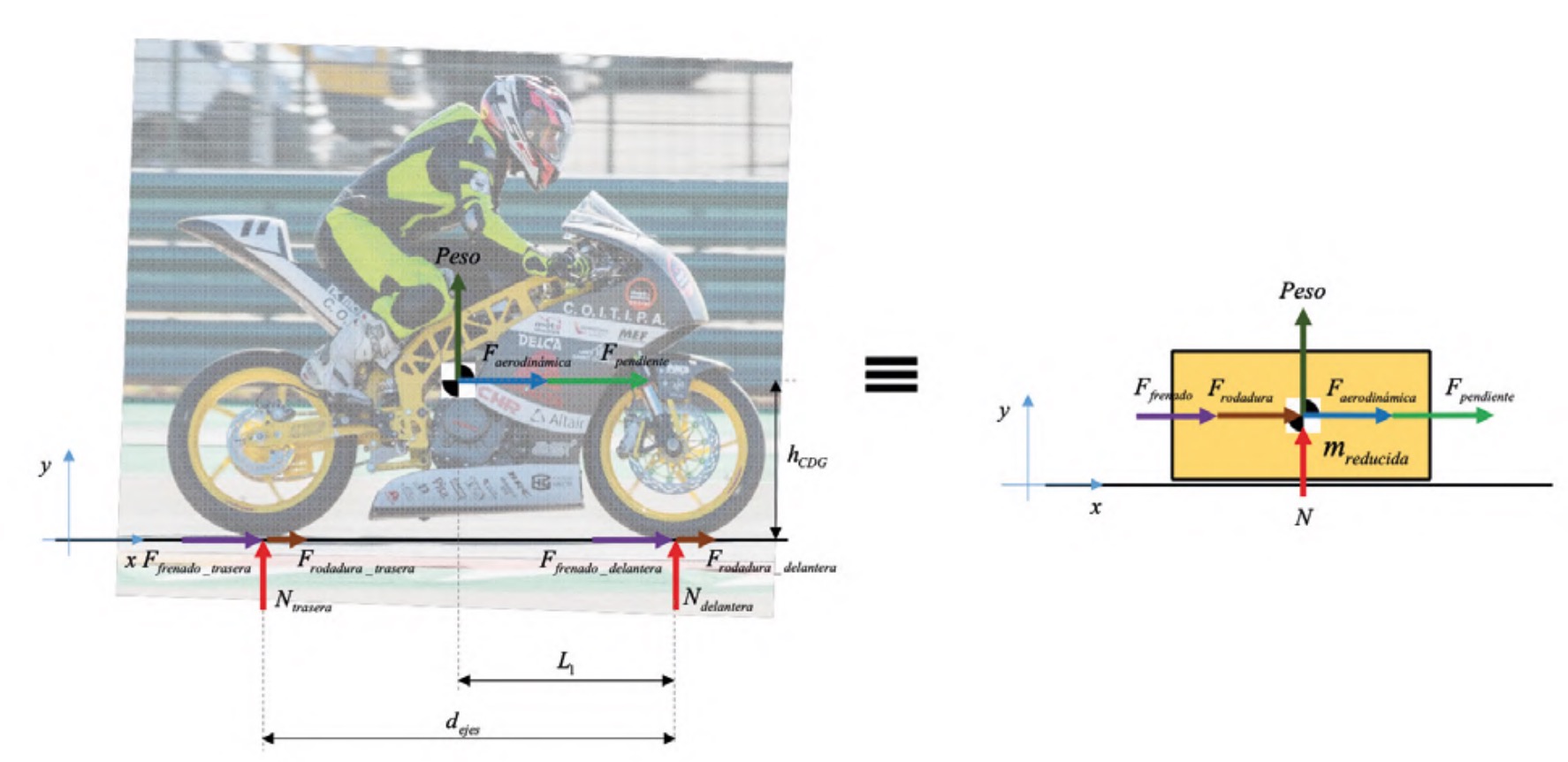
En la zona de frenada, el modelo dinámico a utilizar se puede ver en la figura 3. En este caso, si se quiere determinar el esfuerzo de frenado en cada rueda es necesario realizar una hipótesis de como reparte el piloto la frenada entre los dos ejes, y, en consecuencia, que rueda llegará antes al límite de adherencia. Sin embargo, el análisis es más sencillo, dado que, como una motocicleta es un vehículo con una distancia entre ejes pequeña y un CDG relativamente alto en comparación, la deceleración más limitante es casi siempre la asociada al levantamiento de la rueda trasera (Massaro, 2022). Esta deceleración puede calcularse con la expresión (14), suponiéndola constante durante toda la frenada, y no necesita realizar ninguna hipótesis sobre el reparto de frenada entre los dos ejes.
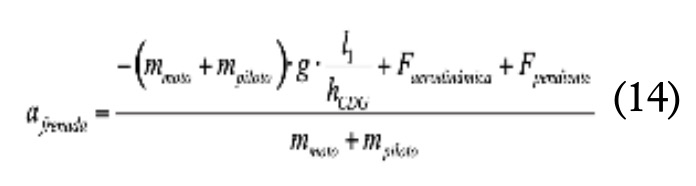 Se considerará que el límite de la operación de frenado es la detención completa de la motocicleta con la expresión (15).
Se considerará que el límite de la operación de frenado es la detención completa de la motocicleta con la expresión (15).
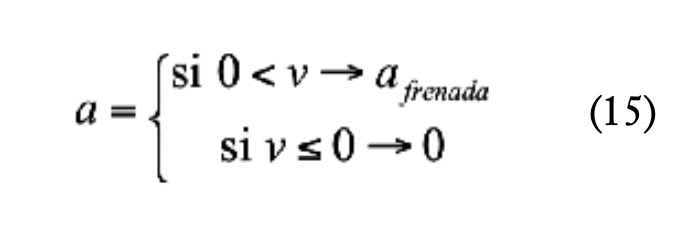 3.3. Obtención del punto óptimo de frenada
3.3. Obtención del punto óptimo de frenada
Teniendo en cuenta las condiciones de contorno indicadas al final de la recta y que el punto de frenado está situado dentro de la recta, se utilizará una variante mejorada del algoritmo de bisección que permite calcular raíces de una función de una variable en un intervalo conocido llamado algoritmo Illinois (McNamee, 2013). La función de la que hay que obtener la raíz será la indicada en la expresión (16), donde vfinal_deseada es la velocidad a la que se toma la siguiente curva y vfinal es la velocidad al final de la recta tras frenar en el punto de frenado xfrenado.
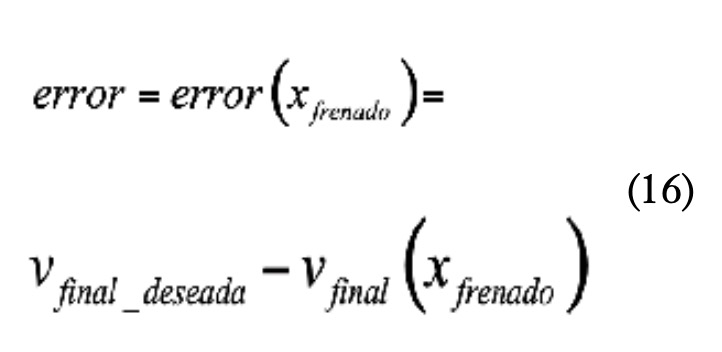 La velocidad al final de la recta se obtiene simulando la dinámica en la recta con un punto de frenado, que actúa como variable independiente. El algoritmo Illinois va probando distintos puntos de frenado hasta que encuentra aquel que consigue una solución cuyo error está suficientemente cerca de cero y supone un incremento de distancia del punto de frenado por debajo de una tolerancia establecida. También tiene un límite máximo de evaluaciones de función para evitar que el coste computacional se dispare.
La velocidad al final de la recta se obtiene simulando la dinámica en la recta con un punto de frenado, que actúa como variable independiente. El algoritmo Illinois va probando distintos puntos de frenado hasta que encuentra aquel que consigue una solución cuyo error está suficientemente cerca de cero y supone un incremento de distancia del punto de frenado por debajo de una tolerancia establecida. También tiene un límite máximo de evaluaciones de función para evitar que el coste computacional se dispare.
3.4. Integración
Dado que la ecuación diferencial a manejar no presenta discontinuidades, se ha utilizado un integrador Runge-Kutta explícito de segundo orden (Süli, 2003), porque tiene un coste muy bajo y una precisión aceptable. Se ha implementado una variante del mismo donde la integración continúa, siempre y cuando la velocidad de la motocicleta sea positiva y no se haya llegado al final de la recta. Las dos variables independientes que hay que integrar 3.4. Integración Dado que la ecuación diferencial a manejar no presenta discontinuidades, se ha utilizado un integrador Runge-Kutta explícito de segundo orden (Süli, 2003), porque tiene un coste muy bajo y una precisión aceptable. Se ha implementado una variante del mismo donde la integración continúa, siempre y cuando la velocidad de la motocicleta sea positiva y no se haya llegado al final de la recta. Las dos variables independientes que hay que integrar son la posición x y la velocidad v. Para evitar que la integración genere un movimiento hacia atrás en la recta, cuando se detecte que dicha velocidad es negativa, se cambiará su valor por cero.
4. Simulación de pruebas
En esta sección se describirán los test simulados y los resultados obtenidos.
4.1. Test de frenado
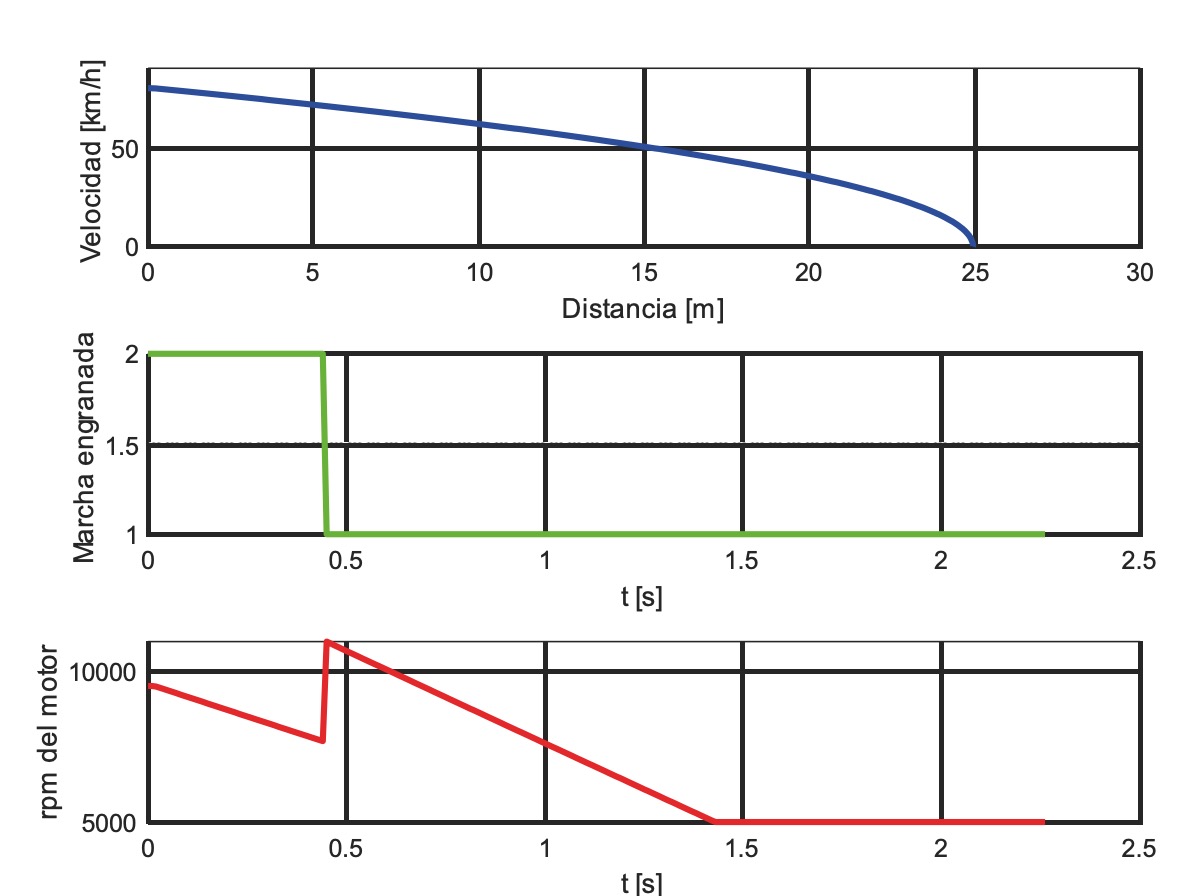
El test de frenado de la competición Motostudent consiste en que la motocicleta, circulando a una velocidad igual o mayor a 80 km/h y sobre una superficie de asfalto con pendiente nula frene hasta detenerse completamente en el menor espacio posible y sin caerse. Si la motocicleta circula a una velocidad menor a 80 km/h tendrá una penalización, y puede considerarse nulo el intento. Cada equipo tiene dos oportunidades para realizar este test, y es puntuable el mejor resultado obtenido.
Se ha realizado la simulación del test con las condiciones indicadas y se ha obtenido el resultado de la figura 4. La frenada se realiza en 24,94 m y dura 2,26 s.
4.2. Test de aceleración
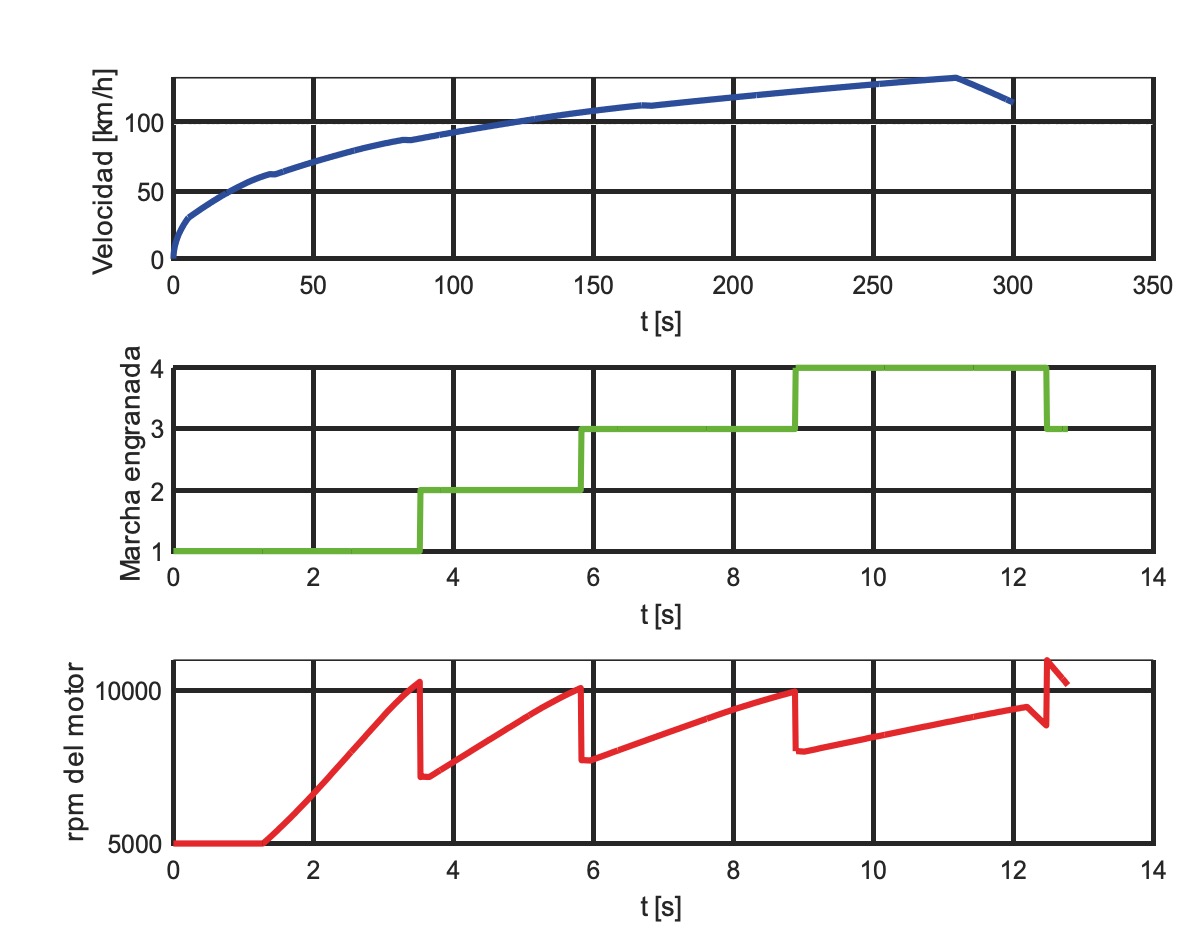
El test de aceleración consiste en que la motocicleta realice una aceleración desde parado sobre una superficie de asfalto con pendiente nula y recorra 150 m en el menor tiempo posible sin caerse. Nuevamente, cada equipo tiene dos oportunidades para realizar este test, y es puntuable el mejor resultado obtenido.
Se ha realizado la simulación del test con las condiciones indicadas y adelantando un poco el CDG respecto a la posición centrada para un pilotaje neutro, hasta que el eje delantero cargue con el 60% del peso. Esto es así porque se ha observado que los pilotos adelantan significativamente su posición sobre la moto para realizar esta maniobra. Tras la simulación, se ha obtenido el resultado indicado en la figura 5. La aceleración se realiza en 8,33 s, alcanzando una velocidad de 108,8 km/h en ese instante.
4.2. Velocidad máxima en el circuito
La obtención de la velocidad máxima en el circuito no se consigue en una prueba específica si no que se produce durante la carrera. En la parte final de la recta más larga del circuito, la situada entre las curvas 15 y 16, se dispone de una fotocélula que registra la velocidad de paso de las motocicletas. Adicionalmente, se dispone de un sistema GPS que también da una lectura de la velocidad instantánea en esa zona.
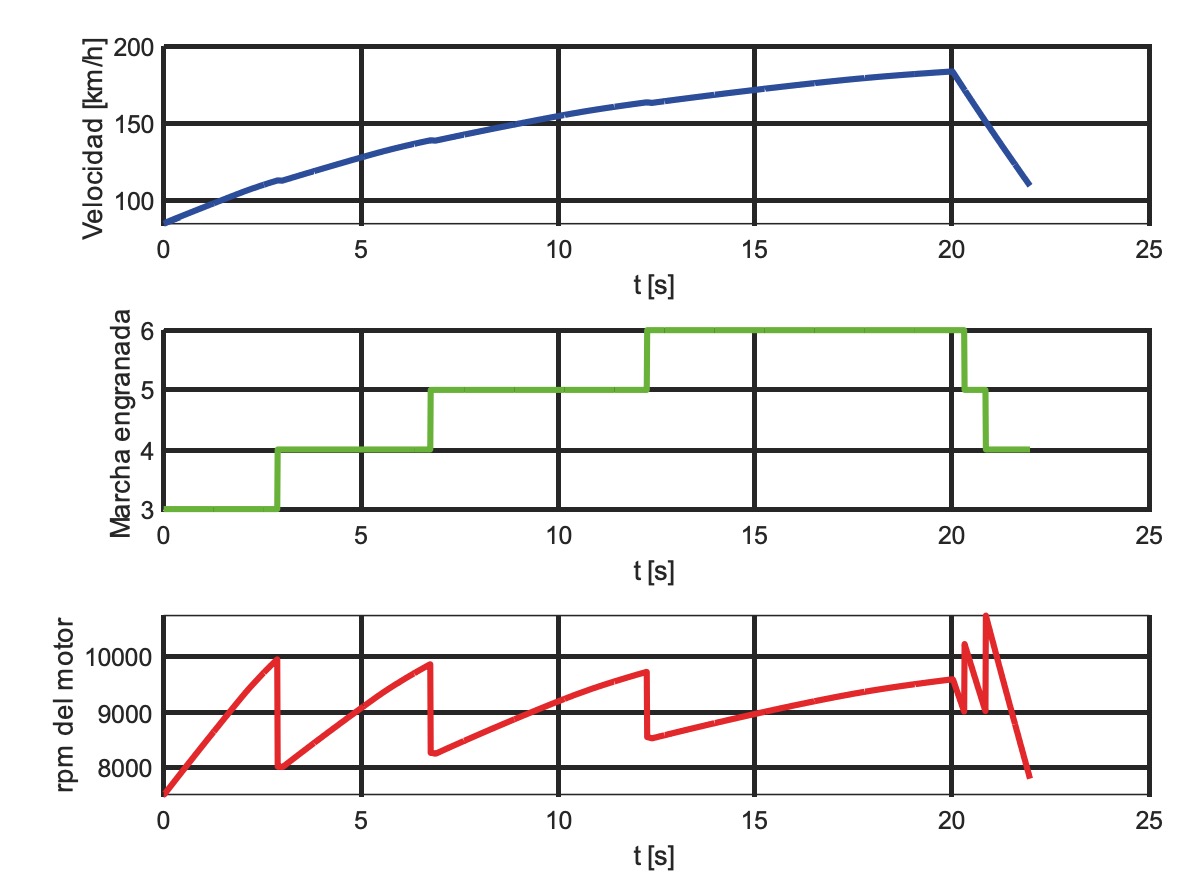
Entonces, para realizar la simulación, se considerará que se inicia la recta a una velocidad de 85 km/h en tercera marcha, se recorrerán 902,7 m subiendo hasta sexta marcha y la velocidad al final será de 110 km/h circulando en cuarta marcha. Estos datos están sacados de la observación de los datos recogidos por el sistema de adquisición de datos que equipaba la motocicleta.
Se ha realizado la simulación con las condiciones indicadas y se ha obtenido el resultado indicado en la figura 6. La velocidad máxima alcanzada es de 183,77 km/h.
5. Validación con resultados experimentales
Para determinar la exactitud y la fiabilidad de los resultados obtenidos por la simulación, se compararán con los resultados obtenidos por el equipo Bizkaia ESI Bilbao en los test realizados durante la quinta edición de la competición Motostudent, celebrada en octubre de 2018.
En el test de frenada, se realizaron dos intentos nulos por iniciar la frenada a una velocidad muy inferior a 80 km/h. Sin embargo, como la organización de la competición informa de esa velocidad, se ha rehecho la simulación con la velocidad de uno de los intentos (61,7 km/h), y se ha obtenido una distancia de frenado de 14,95 m, mientras que, en la realidad, se consiguió frenar en 16,6 m.
En el test de aceleración, se ha cogido el mejor de los dos intentos, en el que se consiguió acelerar en 7,18 s frente a los 8,33 s que arroja la simulación.
Para determinar la velocidad máxima en el circuito, se sabe que esta se da en la parte final de la recta más larga, la situada entre las curvas 15 y 16. En esa zona, se dispone de una fotocélula que registra la velocidad de paso de las motocicletas. Adicionalmente, también se dispone de un sistema GPS que da una lectura de la velocidad instantánea en esa zona. Durante la carrera, la motocicleta considerada alcanzó una velocidad máxima de 182,1 km/h, mientras que la simulación predice 183,77 km/h. 6.
Conclusiones
La simulación del modelo planteado genera unos resultados cercanos a los reales en las tres pruebas simuladas. En el caso del test de frenada, la distancia de frenado real tiene el 11% de error respecto a la obtenida de la simulación. Pero este resultado tiene cierta variabilidad debida, principalmente, a que la actuación del piloto es decisiva, pero no repetible, puesto que nunca frena exactamente igual que la vez anterior ni pasa a la misma velocidad por el punto de frenada. El test de aceleración muestra un error del 13,8% respecto a los resultados obtenidos de la simulación. Nuevamente, esta prueba está afectada por la actuación del piloto, sobre todo, en el arranque, pellizcando el embrague, haciéndolo deslizar en cada cambio de marcha (acción que no es posible emular con precisión en la simulación) y porque mueve su posición sobre la moto respecto a la posición neutra.
En el caso de la velocidad máxima, está menos influida por la actuación del piloto y tiene mucha más dependencia de la longitud de la recta y de las prestaciones puras de la motocicleta, por lo que tiene mayor repetibilidad, la cual se observa en la situación vuelta a vuelta recogida en el sistema de adquisición de datos. Esto hace que la simulación obtenga una estimación de la velocidad máxima alcanzable con un error menor del 1%. Este error se considera muy bajo, teniendo en cuenta las circunstancias, lo que, sumado a la alta repetibilidad de la medida, valida la simulación planteada como método de estimación de la velocidad máxima alcanzable. El uso de este método de estimación simplifica la elección del desarrollo a utilizar en la transmisión por cadena (aunque no lo determine totalmente) sin necesidad de comprar y probar muchos desarrollos diferentes en el circuito.
Estos resultados sugieren que la adaptación de este modelo a la simulación de una motocicleta eléctrica de competición sin embrague ni caja de cambios probablemente pueda generar una simulación más precisa de estas pruebas. 7.
Agradecimientos
Se agradece enormemente el apoyo a este trabajo por parte del Ministerio de Ciencia e Innovación del Gobierno de España, en el marco del proyecto PID2021- 124677NB-I00.
Referencias
Cossalter V., Da Lio M., Lot R., Fabbri L. (1998). Simulation and performance evaluation of race motorcycle dynamics based on parts of real circuit. Power Two Wheels International Conference, Pisa, Italia.
Eksergian, R. (1930). Dynamical analysis of machines. Journal of the Franklin Institute, 209(4), 503-531.
Gadola, M., Chindamo, D. (2019). Experiential learning in engineering education: The role of student design competitions and a case study. International Journal of Mechanical Engineering Education, 47(1), 3-22.
Hauser, J, Saccon, A. (2006). Motorcycle modeling for high-performance maneuvering. IEEE Control Systems Magazine, 26(5), 89-105.
Lesina, F. (2022). Implementation of the motorcycle rider control strategies [Master Thesis, Universidad Politecnico di Milano].
Luque, P., Alvarez, D., Vera, C. (2004). Ingeniería del automóvil. Sistemas y comportamiento dinámico. Ed. Paraninfo.
Massaro, M., Lovato, S. (2022). The optimal trajectory of road vehicles on straights. 2022 IEEE 61st Conference on Decision and Control (CDC), Cancun, Mexico.
McNamee, J.M., Pan, V.Y. (2013). Chapter 7 – Bisection and Interpolation Methods. Studies in Computational Mathematics 16, 1-138.
Süli, E., Mayers, David F. (2003). An Introduction to Numerical Analysis. Cambridge University Press.

