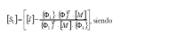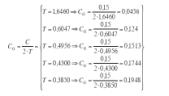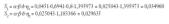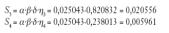Cálculo estructural con hipótesis sísmicas
RESUMEN
El proyectista de estructuras debe considerar a menudo entre las hipótesis de carga las de tipo sísmico, bien porque la zona donde se ubicará el edificio tiene riesgo de sufrir un terremoto o bien porque el uso o características de la estructura obligan a considerar posibles cargas asimilables a un movimiento sísmico. El presente artículo de dinámica estructural es la aplicación de dos métodos de cálculo de los periodos de vibración de una sencilla estructura aporticada de hormigón armado: el de los autovalores y el de Stodola, para comprobar la convergencia y validez de los mismos.
Recibido: 7 de octubre de 2009
Aceptado: 28 de enero de 2011
Palabras clave
Estructuras, sismos, cálculos, hormigón, resistencia sísmica
ABSTRACT
Structural design frequently requires that seismic criteria be considered in load calculations, either because the area where the building is located is at risk of earthquakes or because the use or characteristics of the structure require consideration of possible stresses equivalent to an earthquake. This article on Structural Dynamics considers the application of two methods of calculating the periods of vibration of a simple reinforced concrete portal frame structure, that of the eigenvalues and that of the Stodola, to check the convergence and validity of them.
Received: October 7, 2009
Accepted: January 28, 2011
Keywords
Structures, earthquakes, calculations, concrete, earthquake resistance
Con mucha frecuencia, el proyectista se encuentra frente al cálculo de una estructura en la que, por las características de la zona y del propio edificio, debe aplicar la hipótesis del sismo como una más de entre todas las hipótesis de carga.
Sin embargo, existen otras circunstancias en las que la simple consideración de la zona en la que se asentará el edificio no hace necesario tener en cuenta estas hipótesis. No obstante, las características de la estructura: topología, nivel de ocupación y, sobre todo, el uso al que va a ser destinada, exigen del proyectista la consideración de hipótesis adicionales de carga que tengan en cuenta fenómenos como ataques, sabotajes o cualesquiera otros y que puede llegar a modelizar como un efecto sísmico de determinada intensidad.
En las páginas que siguen van a establecerse los pasos para obtener las fuerzas estáticas equivalentes a aplicar, como una hipótesis más, al cálculo de la estructura. Para ello, y tomando como ejemplo una simple estructura aporticada de hormigón armado, va a procederse, paso a paso, al cálculo de los periodos de vibración por dos procedimientos, analizando después la diferencia entre ellos.
En primer lugar, se procederá a la obtención de los autovalores de la matriz formada por la matriz de rigidez y la matriz de masas.
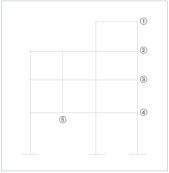
Posteriormente, se repetirá el cálculo aplicando el método de Stodola (figura 1 y figura 2).
Aplicación del método de las matrices de rigidez y de masas
El sistema dispone de cinco grados de libertad. Los cuatros primeros se desplazan horizontalmente y el quinto lo hace de forma vertical.
El primer paso es calcular la matriz de flexibilidad, cuyos elementos son los fi,j, tales que fi,j representa el desplazamiento que experimenta el punto j cuando se aplica una fuerza unitaria al punto i.
Para obtener los valores fi,j se introduce la estructura en un programa adecuado. En este caso, se ha utilizado el clásico Tens para PC, con E = 2,1 · 106 y δ = 2,3 (estructura de hormigón), con las siguientes hipótesis de carga:
– Primera hipótesis: aplicación de una fuerza horizontal en el nudo nº 1 de 104 Kp.
– Segunda hipótesis: aplicación de la misma carga horizontal en el nudo nº 2.
– Tercera hipótesis: igual en el nudo 3.
– Cuarta hipótesis: igual en el nudo 4.
– Quinta hipótesis: aplicación de una carga vertical de 104 Kp en el nudo número 5.
Los desplazamientos obtenidos en cada nudo i, aplicando la primera de las cinco hipótesis de carga son:
δ1(x) = 49,156 m; δ2(x) = 28,5158 m; δ3(x) = 16,8648 m; δ4(x) = 4,3883 m; δ5(y) = 0,117 m.
Con lo que los elementos de la primera fila de la matriz f (matriz de flexibilidad) son:
De la segunda hipótesis de carga se obtienen los desplazamientos siguientes:
δ1(x) = 28,5158 m; δ2(x) = 27,0703 m; δ3(x) = 16,8037 m; δ4(x) = 4,3855 m; δ5(y) = 0,2322 m;
Los elementos de la segunda fila de la matriz son entonces:
Precediendo de forma análoga y recordando que la matriz de flexibilidad es simétrica (por tanto, fi,j = fj,i como puede comprobarse en los resultados que arroja el listado del ordenador ), se obtienen los restantes elementos de la matriz f:
f31 = f13 = 0,00168648 m/t
f32 = f23 = 0,00168037 m/t
f33 = 0,0015557 m/t
f34 = 0,00043616 m/t
f35 = 0,0000194 m/t
f41 = f14 = 0,00043882 m/t
f42 = f24 = 0,00043855 m/t
f43 = f34 = 0,00043616 m/t
f45 = 0,00001155 m/t
Los elementos de la última fila se obtienen aplicando una fuerza vertical de 104 t en el punto 5 y midiendo los desplazamientos horizontales δ1, δ2, δ3, δ4 y el vertical δ5 (esta fila se obtiene del listado de desplazamientos con la hipótesis de carga núm. 5):
f51 = f15; f52 = f25; f53 = f35; f54 = f45; f55 = 0,00006917
La matriz de flexibilidad resulta entonces:
con sus elementos en metros/tonelada fuerza.
La matriz de masas se obtiene a partir del peso propio y la sobrecarga de cada nivel de la estructura. Así, para el nivel 1 se obtiene:
p.p.= volumen · δ = sección · longitud · δ = 0,3 · 0,4 · 5 · 2,5 = 1,5 t de fuerza
s. u. = 8 t/m · 5 m = 40 t de fuerza ⇒ q = 41,5 t de fuerza
Para pasar a unidades de masa dividimos entre g, resultando, m11 = 4.2301 Ku.t.m. Procediendo de forma análoga con los otros niveles, se obtiene:
Obtenemos así la matriz de masas siguiente:
La matriz de rigidez es la inversa de la matriz de flexibilidad (también llamada matriz de deformaciones), es decir, k = (f)-1
Invirtiendo la matriz f con un programa de ordenador, se tiene:
en la que se han omitido los elementos de la parte inferior, por ser simétrica (kij = kji).
Las pulsaciones de la estructura son los autovalores de la matriz A = k –m · ω 2.
Operando se tiene:
Sacando los siguientes factores comunes: 4,2304 en la primera fila; 13,6493 en la segunda; 13,6493 en la tercera; 17,3675 en la cuarta y 13,8022 en la quinta, resulta la matriz:
Desarrollando el determinante de la matriz anterior e igualando a cero, se obtiene la ecuación característica. Sus soluciones son los autovalores buscados. Este paso, tremendamente laborioso, se simplifica al máximo utilizando un programa de cálculo matricial. El resultado del cálculo por ordenador es el siguiente:
ω 2 = 14,57277 ⇒ω = 3,8174 rd/s
ω 2 = 191,8007 ⇒ω = 13,8492 rd/s
ω 2 = 107,9455 ⇒ω = 10,3897 rd/s
ω 2 = 1055,064 ⇒ω = 32,4817 rd/s
ω 2 = 302,1367 ⇒ω = 17,3821 rd/s
Y como ω = 2 . π . f = 2 . π / T ⇒ T = 2 . π / ω, resultan los siguientes periodos de vibración (en segundos):
T1 = 1,6459
T2 = 0,6048
T3 = 0,4537
T4 = 0,3615
T5 = 0,1934
Disponiendo de un programa para el cálculo de autovalores (o ecuación característica de una matriz), este es el procedimiento más rápido y exacto que se resume en:
1. Obtención de la matriz f, mediante un programa de cálculo matricial de estructuras (en este caso ha sido utilizado Tens).
2. Inversión de la matriz de flexibilidad para obtener la matriz de rigidez k.
3. Obtención de la matriz m de masas (su cálculo es inmediato disponiendo de las cargas).
4. Cálculo de los autovalores de la matriz.
Aplicación del método de Stodola
Anteriormente han sido obtenidas las matrices de flexibilidad f y la de masas m, llamando D a la matriz cuadrada de orden 5, producto de las dos anteriores, y siendo
Detenemos aquí el proceso por ser ya pequeñas las diferencias que aparecen entre los valores de dos tanteos sucesivos. Tenemos entonces:
lo que representa un error del 0,54% respecto al valor obtenido por el primer método.
Obtengamos ahora los resultados para el segundo modo de vibración:
[M]: matriz de masas
El cálculo de la matriz S1 es inmediato. A partir de esta matriz y como la matriz D es conocida, puede calcularse [D1]=[D].[S1], que resulta ser una matriz cuadrada de orden 5.
Detenemos aquí el proceso y tenemos:
lo que representa un error del 1,0665% respecto al valor de T2 obtenido por el procedimiento de los auto[[k] – [m]·w]
valores de la matriz
Se aprecia entonces que, el error que arroja el método de Stodola va aumentando con los modos de vibración, o lo que es lo mismo, para obtener las mismas precisiones en los sucesivos modos, hemos de ir aumentando el número de iteraciones de un modo al siguiente.
Es necesario obtener ahora los vectores de forma, que son los autovectores de la matriz
[[k] – [m]·w]
para poder aplicar la morma Sismorresistente.
El cálculo de la matriz S1 es inmediato. A partir de esta Sustituyendo w1, w2, w3, w4y w5 en la matriz anterior, se matriz y como la matriz D es conocida, puede calcularse obtiene el siguiente sistema de ecuaciones en forma matricial:
Para w = 3,8174 rd/s
Este sistema es indeterminado. Da un valor a una de las variables, se elimina una de las ecuaciones y queda un sistema compatible determinado.
Haciendo a1 = 1, se tiene
cuya solución es:
Se observa la casi coincidencia con el vector de forma obtenido por el método de Stodola.
Procediendo de forma análoga con w = 13,8492 rd/s, se obtiene
Se observa la correspondencia entre los resultados obtenidos mediante el método de Stodola y el de los autovalores y autovectores, pero solo hasta el segundo modo. A partir del modo 3, Stodola da los mismos valores para las componentes del vector de forma normalizado. Esto sucede en ocasiones con el método de Stodola, sobre todo cuando existen grados de libertad desacoplados.
Como ya ha sido comentado, es más exacto, a partir de un programa informático que nos dé los autovalores de la matriz, crear otro que sustituya estos valores en la misma y resuelva los n sistemas de n-1 ecuaciones con n-1 incógnitas. En efecto, los n sistemas de n ecuaciones son indeterminados, para resolverlos se da el valor 1 a la primera variable, quedando el sistema con n-1ecuaciones y n-1 incógnitas.
Aplicación de la norma sismorresistente
Para la aplicación de la norma, van a utilizarse los valores del cálculo dinámico obtenidos mediante un programa elaborado en la Escuela Politécnica Superior por el profesor ingeniero don Elías Benito y modificado, posteriormente, por el autor de estas notas y por el ingeniero don Alfredo Valencia. Este programa permite, además, de una manera muy rápida, obtener las fuerzas estáticas equivalentes a aplicar en la estructura, con la introducción de los desplazamientos de todos los nudos maestros obtenidos para cargas unitarias en cada uno de ellos (es decir, exige disponer de la matriz de flexibilidad y que pueden obtenerse fácilmente a partir de cualquier programa de cálculo matricial de estructuras), el grado sísmico de la zona, el riesgo sísmico, el factor de respuesta y el factor de cimentación.
En este apartado va a realizarse el cálculo paso a paso.
El resultado de los valores del cálculo dinámico ha sido el siguiente:
Modos del 1 al 5.
Componentes del vector de forma normalizado. Niveles de 1 a 5:
Valores de w:
w1 = 3,817299870692743 rad/s
w2 = 10,38972983896404 rad/s
w3 = 12,67911572394805 rad/s
w4 = 14,61415356692948 rad/s
w5 = 16,31168518604988 rad/s
Valores del periodo de oscilación:
Modo 1: T1 = 1,6460 s
Modo 2: T2 = 0,6048 s
Modo 3: T3 = 0,4956 s
Modo 4: T4 = 0,4300 s
Modo 5: T5 = 0,3850 s
Se considera un grado sísmico de la zona de 8, un riesgo sísmico de 0,99, es decir, un periodo de riesgo de 100 años, un coeficiente para el factor de respuesta de 0,6 y un factor de cimentación de 0,8. Con estos datos se tiene:
F = S · Q
Coeficiente sísmico = S = α ⋅ η ⋅ β ⋅ δ
Factor de intensidad = α = C · R
Cálculo del coeficiente sísmico básico:
Tomando como valor del riesgo sísmico R = 0,99 (periodo de riesgo de 100 años) se tiene para el factor de intensidad:
Factor de distribución η:
Primer modo:
= 1·1,395973 = 1,395973
η2 = 0,8477·1,395973 = 1,183366
η3 = 0,588·1,395973 = 0,820832
η4 = 0,1705·1,395973 = 0,238013
η4 = 0,0075·1,395973 = 0,010470
Segundo modo:
Procediendo de forma análoga se tiene
η1 = -0,8282
η2 = 0,0505·(-0,8282) = -0,0418
η3 = -0,4703·(-0,8282) = 0,3895
η4 = -0,3506·(-0,8282) = 0,2904
η5 = -0,0156·(-0,8282) = 0,0129
Puesto que se obtuvieron los mismos autovalores para el tercer modo que para el segundo, resultan para aquel los mismos factores de distribución.
Coeficiente sísmico:
Primer modo:
Y, análogamente, para el segundo y tercer modos.
Fuerzas estáticas equivalentes:
Para cada uno de los modos, aplicando
Fi,j = Si,j · Qi
siendo Fi,j el coeficiente sísmico para el nivel i en el modo j y siendo Qi la carga en el nivel i, resulta inmediata entonces la obtención de las fuerzas estáticas equivalentes para cada uno de los cinco niveles en los tres modos.
Las solicitaciones que aplicar en la estructura para simular el efecto del sismo se obtienen aplicando la media cuadrática de las fuerzas estáticas equivalentes en cada uno de los modos:
Que son las fuerzas que hay que aplicar a cada uno de los niveles para simular, en el cálculo de la estructura, la hipótesis sísmica considerada.
Nota
Es necesario indicar que en el punto 5 de la estructura que la solicitación debe ser vertical y que, por tanto, y como indica la norma, F ya no es el producto del coeficiente sísmico por la carga Q, sino que F = V · Q = χ · C · Q
Bibliografía
Barbat AH, Bozzo LM (1999). Diseño sismorresistente de edificios. Técnicas convencionales y avanzadas. Reverté. ISBN 978-84-291-2011-0.
Bazán E, Meli Miralla R (1999). Diseño sísmico de edificios. Limusa. ISBN 978-968-18-5349-0.
Sanmartín Quiroga, AF (2008). Curso de ingeniería sísmica I: la acción sísmica. Colegio de Ingenieros de Caminos, Canales y Puertos, Madrid. ISBN 978-84-380-0380-0.
Paz M (1992). Dinámica estructural. Editorial Reverté. ISBN 978-84-291-4854-1
Benavent Climent A (2010). Estructuras IV: hormigón pretensado, edificios en zonas sísmicas, edificios de gran altura, diafragmas horizontales, losas, muros y pilotes. Editorial Universidad de Granada. ISBN 978-84-338-5112-3.
Aenor (1998). Eurocódigo 8. Disposiciones para el proyecto de estructuras sismorresistentes. Parte 1-1: Reglas generales, acciones sísmicas y requisitos generales de las estructuras. UNE-ENV 1998-1-1:1998.
Fernández Gómez J (2001). Evaluación de la capacidad resistente de estructuras de hormigón: ensayos no destructivos y pruebas de carga. Intemac Ediciones. ISBN 978-84-88764-12-6.
Díaz Rodríguez A (2005). Dinámica de suelos. Limusa. ISBN 978-968-18-6779-9.
Ricardo García Reverter
garcibas@telefonica.net Ingeniero de construcción y electricidad, ingeniero técnico industrial, ingeniero técnico de armamento y diplomado en Alta Gestión Logística. Trabaja como ingeniero del Estado en el Ministerio de Defensa.