Cálculo del esfuerzo de viento en apoyos de líneas eléctricas aéreas

Aparte de la intensidad y la frecuencia de aparición del viento, hay que prever las distintas direcciones en que puede actuar y realizar los cálculos considerando las situaciones más desfavorables

El esfuerzo horizontal resultante sobre un apoyo de ángulo (tanto en baja como en alta tensión), se viene calculando como la suma geométrica de dos componentes: una, originada por el tiro mecánico de conductores y cables de tierra a ambos lados del apoyo, y la otra, la originada por efecto del viento sobre el propio apoyo con sus elementos y sobre los conductores y cables de tierra de los vanos adyacentes. El esfuerzo útil del apoyo dado por el fabricante ya descuenta la parte correspondiente de viento reglamentario sobre el mismo.

R = R_T + R_V

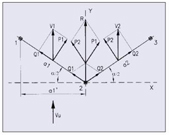
Situándonos en el caso más simple de un apoyo de ángulo, en que los vanos a uno y otro lado son iguales y con el mismo tipo de conductores y tenses, y dejando a un lado el esfuerzo de viento sobre aisladores y otros elementos que pudieran existir en el apoyo, la resultante originada se determina por la suma de sus componentes de tenses y viento.

En este caso, se emplea la fórmula admitida generalmente:

R = 2.T.sen(a/2) + k.cos²(a/2) (1)

siendo:

R = Resultante (en este caso según la bisectriz)

T = Tensión mecánica considerada de todos los conductores a un lado del apoyo

k = Esfuerzo de viento sobre los conductores de ambos semivanos, en sentido de la bisectriz

a = ángulo de desvío de la línea

Si consideramos unicamente el esfuerzo que origina el viento sobre un vano, resulta:

V₁ = V _u·a₁·S(n₁·d₁)·cos(a/2) (2)

siendo:

V_u = presión dinámica de viento sobre 1 m² de silueta de conductor, 50 o 60 daN

a₁= vano en m

S(n₁ .d₁) = silueta total de conductores por m de vano, en m²

o sea:

V₁ = k₁.cos(a/2) (3)

Igual para el otro vano.

Admitiendo que este esfuerzo se reparte en dos mitades a cada apoyo que delimita cada uno de los dos vanos, el esfuerzo de viento total sobre el apoyo será:

R_V = ¹/₂.k.cos(a /2) + 1/2.k.cos(a /2)

R_V = k.cos(a /2) (4)

valor que da resultados mayores que en la (1) al estar el coseno al cuadrado.

Pero esto tampoco es rigurosamente cierto.

Situándonos en la figura 2, (continuando con el caso de un apoyo con vanos compensados), el efecto de viento sobre el vano a₁ es V₁ de valor según la (2). Este esfuerzo lo descomponemos en P₁ perpendicular al vano, y Q₁ en el sentido del vano, teniendo que:

P₁ = V₁.cos(a/2)

Q₁ = V₁.sen(a/2)

teniedo en cuenta la (3):

P₁ = k₁.cos²(a/2)

Q₁ = k₁.sen(a/2).cos(a/2)

lo mismo para el vano a₂.

Ocurre que las componentes respectivas P₁ y P₂ se reparten en dos mitades cada una a sus apoyos que delimitan cada vano, no ocurriendo lo mismo con las componente Q₁ y HQ₂, que se transmiten íntegramente al apoyo (al ser componentes de tiro mecánico sobre el apoyo).

Por consiguiente, la componente de viento sobre el apoyo resultaría ser:

R_V = Q₁.sen(a/2) + Q₂.sen(a/2 )+ 1/2 .P₁.cos(a/2) + 1/2 .P₂.cos(a/2)

o bien:

R_V = (Q₁+Q₂).sen(a/2)+ 1/2 .(P₁+P₂).cos(a/2)

Es el caso hipotético más simple, que en la realidad casi nunca aparece. Analicemos entonces el caso general, cuando los vanos son desiguales, los tenses distintos a cada lado y el viento actuando bajo un ángulo cualquiera.

Erróneamente hay quien piensa que la resultante de mayor valor (suma de tenses más viento) que puede originarse, corresponde a la hipótesis de viento actuando según la bisectriz o según la dirección de la componente de tenses. No tiene que ser así.

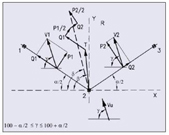
En la figura 3 vemos que el viento actúa bajo un ángulo ?. Siguiendo el mismo razonamiento anterior, sobre el primer vano ejerce una presión V₁ que vale:

V₁ = V _u.a₁.S (n₁.d₁).sen(? -a/2) = k₁.sen(? -a/2)

tal esfuerzo está integrado por una componente “P₁” perpendicular al vano, y una componente “Q₁” en el sentido longitudinal del vano. Estos tendrán por valores respectivos:

P₁ = V₁.sen(? -a/2) = k₁.sen² (? -a/2)

Q₁ = V₁.cos(? -a/2) = k₁.cos(? -a/2).sen(? -a/2)

del mismo modo, para el segundo vano:

V₂ = V _u.a₂.S (n₂.d₂).sen(? + a/2) = k₂.sen(? + a/2)

P₂ = V₂.sen(? + a/2)) = k₂.sen² (? + a/2)

Q₂ = V₂.cos(? + a/2)) = k₂.cos(? + a/2).sen(? + a/2)

los ángulos de orientación de cada una de estas componentes son:

para P₁:100 + a/2

para Q₁: a/2

para P₂:100 – a/2

para Q₂:200 – a/2

la suma geométrica de todas estas componentes añadida a la resultante de tenses “T”, nos dará la resultante total del sistema.

La resultante de tenses:

T = v (T₁² + T₂² –2.T₁.T₂.cos(a) )

Orientada según:

tg ß = (T₁+T₂).tg(a/2) / (T₁-T₂)

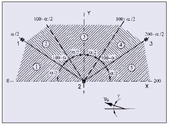
Dependiendo de la incidencia de viento, se pueden presentar cinco casos en que la resultante de viento aparezca en una u otra zona, (figura 4), pudiendo tomar las componentes V y Q valores positivos, negativos o nulos tabla I.

Cuando el apoyo proyectado no es isorresistente, como suele ocurrir casi siempre, por tratarse de apoyos metálicos de sección cuadrada, o apoyos de hormigón de sección rectangular, en los que los esfuerzos disponibles se refieren a sus caras, hay que tener previsto un coeficiente de corrección k_R, dependiente de la orientación de la resultante con respecto a la dirección del esfuerzo disponible del apoyo.

Ocurre entonces que el valor de la resultante máxima se modifica en función del ángulo, de manera que puede aparecer (y así ocurre) otro valor de resultante (menor) bajo otro ángulo distinto, pero al aplicarle el k_R se obtiene un valor resultante mayor.

En estos casos, y para apoyos de sección cuadrada, añadimos el coeficiente k_R:

k_R = sen f+ cos f

para apoyos de sección rectangular (apoyos de hormigón) con coeficiente de esfuerzo secundario e%:

k_R = (100/e).sen f+ cos f

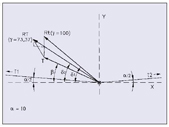
Para ver hasta que punto pueden llegar las diferencias entre el cálculo de una u otra forma, comprobemos (a modo de ejemplo) el caso de una línea, trifásica, simple circuito, con conductor LA145.

Ejemplo:

T₁ = 1.700 daN

T₂ = 1.200 daN

a₁= 250 m

a₂= 150 m

a= 10^g00

Con el método clásico y viento ?= 100^g00

T = v(T₁² + T₂² –2.T₁.T₂.cos(a) )

T = 1643,80 daN

tg ß= (T₁+T₂).tg(a/2) / (T₁-T₂)

ß= 27,26

V = k.cos²(a/2) = 563,51 daN

Rt = v(V+T.sen ß) ² +( T.cos ß)²

Rt = 1946,50 daN

cos d= T/Rt . cos ß

d= 44^g22

f= 100 – d= 55^g78

k_R = 1,4084

RT = Rt .k_R = 2.741,48 daN

esfuerzo que habría de tener disponible el apoyo.

Partiendo de este ejemplo de cálculo por el método tradicional, realizamos el cálculo según el método propuesto, para todos los valores del ángulo de incidencia del viento, (desde ?= 0^g hasta ?= 200^g) encontrando un valor de ?tal, que el esfuerzo resultante R_T.k_R sea el mayor de todos. Este esfuerzo (2) lo comparamos con el cálculado por el método tradicional (1) (para ?= 100^g). Como consecuencia encontramos que cuando el viento incide bajo un ángulo ?= 73^g40, la resultante con viento, que actuaría sobre el apoyo, considerando un nuevo k_R=1,3843 (menor incluso que en el cálculo del ejemplo), resulta ser de RT = 2952,12 daN, lo que supone diferencia entre uno y otro cálculo de 210,64 daN, o bien un 7,68 %.

La tabla 2 se ha elaborado teniendo presente los datos del ejemplo anterior, variando únicamente el ángulo de línea a, para distintos valores, con la finalidad de ver como afectan los resultados.

Línea AT trifásica S/C sobre apoyo de sección cuadrada (e = 1,00)

conductor LA-145

T₁ = 1.700 daN

T₂ = 1.200 daN

a₁= 250 m

a₂= 150 m

d = 15,75 mm

Realizando comprobaciones para distintas situaciones de otros tantos tipos de líneas, se pueden encontrar diferencias de importancia.

Así, en el caso de un apoyo de sección cuadrada, en alineación (a = 0^g00), con cadenas de amarre, con tenses y vanos compensados, la diferencia a considerar en el esfuerzo útil necesario en el apoyo, calculando el esfuerzo transversal con viento perpendicular al vano (? = 100^g00), difiere en un 20 % con relación al calculado considerado el viento incidiendo bajo un ángulo de ? = 75^g00.

Más acusadas son estas diferencias cuando se trata de apoyos de hormigón, de sección rectangular, en que la influencia del coeficiente k_R es mayor, pudiendo llegar a alcanzar diferencias, en el caso de apoyos de alineación, de cerca del 50 %.

Caso de líneas trenzadas de baja tensión sobre apoyos de hormigón (e = 0,60)

Estas diferencias son mucho más acusadas cuando se trata de líneas de baja tensión, en que los conductores presentan grandes secciones al efecto de viento y, si además, como suele ocurrir, se emplean postes de sección rectangular, con coeficientes de resistencia secundario e < 1, aún se acentúan más estas diferencias. Tal es (por ejemplo) el caso de un apoyo de hormigón de sección cuadrada, con e = 0,6 y cable trenzado de 3×50+54,6, tensado a 500 daN, soportando dos vanos de 60 m. En la tabla 3 se observan que las diferencias se aproximan al 50 %. En el caso más simple, supuesto un apoyo de alineación (a^g = 0,00) con amarre del conductor, si lo calculamos con un viento perpendicular al vano (como se suele hacer) necesitaríamos un esfuerzo útil en el apoyo de 110,70 daN, ya que k_R = 1, mientras que si consideramos un viento incidiendo bajo un ángulo ?^g= 67,22 el esfuerzo sobre los conductores sería de 96,34 daN, pero al aplicar el coeficiente corrector por orientación de esta resultante respecto del apoyo (k_R = 1,6902), sería necesario un esfuerzo útil en el apoyo de 162,93 daN (en dirección de la cara de máximo esfuerzo), lo que supone un incremento en el esfuerzo a disponer en el apoyo del 47,18 %

Líneas trenzadas de baja tensión sobre apoyos de hormigón (e = 0,60)

conductor RZ 3×50+54,6

T₁= 500 daN

T₂= 500 daN

a₁= 60 m

a₂= 60 m

d = 36,90 mm Vu = 50 daN/m²

Todas las consideraciones expuestas anteriormente son aplicables a cualquier tipo de apoyo (excepto apoyos con cadenas de suspensión), incluso en estrellamientos y finales de línea.