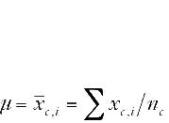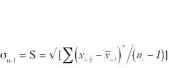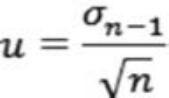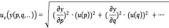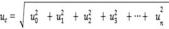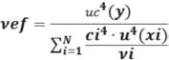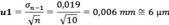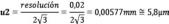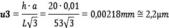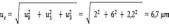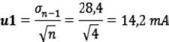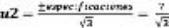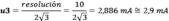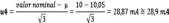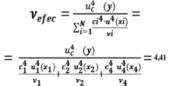La incertidumbre en la medida de una magnitud y el método de Montecarlo
RESUMEN
El artículo describe el tratamiento y conocimiento de la incertidumbre
asociada a la medida de una magnitud según las directrices marcadas
por The Guide to the Expression of Uncertainty in Measurement
(GUM) y de cómo influye esta incertidumbre en el conocimiento
de la magnitud medida. Hoy en día el conocimiento es fundamental.
Es la clave para el éxito en la empresa mantener y generar innovación,
ser competitivos. Cada vez se cuantifica más, el conocimiento
es número, el conocimiento es medir, el conocimiento son cifras. Si
esas cifras no se expresan adecuadamente pueden dar lugar a diferentes
interpretaciones y en algunos casos, confusiones. Es, por
tanto, necesario que las medidas se realicen con una calidad que
viene determinada por el cálculo de incertidumbres asociado a la
medida realizada. En el artículo se explica la evolución en el tratamiento
de una medida, desde el uso del concepto de error de medida,
ya obsoleto, al concepto de incertidumbre de medida. Se repasan
los diferentes tipos de incertidumbre así como los llamados factores
de influencia. Además, se propone usar el método de Montecarlo
aplicado en hoja de cálculo Excel como método alternativo sencillo
para cuando el tratamiento convencional del cálculo de incertidumbres
por el método de la propagación de varianzas se hace
demasiado complicado por tener que trabajar con un número elevado
de variables de entrada, o se necesite validar un procedimiento
clásico de medida de incertidumbres por el método de la propagación
de varianzas con el uso de otro método alternativo con el objeto
de comparar los resultados y poder realizar una validación.
Recibido: 3 de septiembre de 2012
Aceptado: 1 de febrero de 2013
Palabras clave
Medición, incertidumbre, matemáticas, cálculos
ABSTRACT
The article describes the processing and knowledge of the uncertainty associated to magnitudes measurement according to the GUM guidelines. Nowadays knowledge is essential. It is the key to obtain results, to generate innovation and to become competitive. Increasingly more quantified, knowledge is number, knowledge is measured, knowledge are figures. If these figures are not expressed properly, they can result in different interpretations and in some cases, confusion. It is, therefore, necessary that the measures are carried out with a quality that is determined by the calculation of uncertainties associated to the performed measurement. This article discusses the evolution in the treatment of a measure, from the use of the concept of measurement error, now obsolete, to the concept of uncertainty of measurement. The different types of uncertainty as well as the so-called factors of influence are reviewed. It also intends to use the Monte Carlo method applied in Excel spread sheet as an easy alternative when conventional treatment of the calculation of uncertainties by the method of propagation of variances becomes too complicated because of the need of working with a large number of input variables, or it is needed to validate a procedure classic measure of uncertainty by the method of propagation of variances with the use of other alternative method in order to compare the results and to be able to perform validation.
Received: September 3, 2012
Accepted: February 1, 2013
Keywords/P>
Measurement, uncertainty, mathematics, calculations
La importancia de la media
Contar, pesar y medir son actividades que se remontan a los orígenes de la humanidad. Ya en los tiempos remotos del Egipto faraónico, hace más de 5.000 años, la construcción de las grandes pirámides requería un sistema de medición muy refinado. A aquellos que olvidaban su deber de calibrar el patrón de longitud las noches de luna llena se les aplicaba la pena de muerte. Tal era el castigo derivado de la norma establecida por el grupo de arquitectos reales, responsables de la construcción de templos y pirámides en el antiguo Egipto de los Faraones, 3.000 años a. C. (Pachón, 2002). Su patrón de longitud era el “codo real”, basado en la magnitud del antebrazo del faraón. El codo maestro estaba realizado en granito negro y era el patrón con el cual se comparaban y calibraban todas las varas de codo empleadas en la obra. El no hacerlo se pagaba con la muerte.
Actualmente, los intercambios comerciales exigen la certificación de la calidad de los productos siguiendo normas internacionales como la ISO 9001-2000 para gestión de calidad, y la ISO 22000-total para la gestión de seguridad alimentaria. Las especificaciones de los productos deben reflejar la calidad de los resultados de la medición, lo que implica proporcionar una medida de la exactitud y de su grado de dispersión o incertidumbre asociada.
Por ejemplo, cada vez más un mayor número de decisiones se basan en análisis químicos cuantitativos, bien sea para expresar los rendimientos de procesos, para saber si las características de los materiales están de acuerdo con las especificaciones o para valorar económicamente y después, en función de los resultados numéricos obtenidos, tomar decisiones. En los resultados de una medición no se pueden duplicar las interpretaciones, el resultado es único, con la incertidumbre que lleva asociada la medida.
El cliente recurre a un laboratorio porque necesita resolver un problema y confiar en los resultados obtenidos. Es el analista quien debe garantizar que los resultados son adecuados para el uso destinado, para resolver el problema del cliente y es también quien debe expresar estos resultados de manera que el cliente pueda entenderlos y utilizarlos para tomar decisiones.
Concepto de medida
Una medida proporciona información sobre una propiedad de algo. Puede indicar cuán pesado es un objeto, su temperatura o su longitud. Una medida proporciona un número para esa propiedad. Las medidas siempre se realizan utilizando algún tipo de instrumento: reglas, cronómetros, termómetros etcétera.
La calidad de la medida viene determinada por la incertidumbre asociada. Metrológicamente, la incertidumbre es un parámetro asociado al resultado que expresa la desviación que puede tener el mensurando. Por medio de la incertidumbre se expresa la duda acerca de la validez de un resultado. Por tanto, expresa la calidad de la medida realizada.
Inicios del cálculo de la incertidumbre de medida
El concepto de incertidumbre asociada a una medida es relativamente moderno. Empieza a desarrollarse a finales de la década de 1970 y a principios de la de 1980. Hasta entonces siempre se había utilizado el concepto de error pero este, al igual que el cálculo de errores, ya ha quedado obsoleto.
Fue a principios de 1978 cuando el Comité Internacional de Pesas y Medidas (CIPM) se dio cuenta de la necesidad de definir de forma razonada y coherente el cálculo de las incertidumbres. Entonces el CIPM mandó a su oficina la BIPM que elaborara una encuesta para mandar a distintos centros e institutos científicos, y estos respondieron enseguida planteando el mismo tipo de cuestiones. Después de esto, el CIPM mandó a ISO que estudiara el tema y de ahí salió en 1980 la primera recomendación sobre el cálculo de la incertidumbre de medida, que no ocupaba más de una hoja. Posteriormente, se dedicaron conjuntamente al mismo tema siete organizaciones internacionales: la Oficina Internacional de Pesas y Medidas (BIPM), la Comisión Internacional de Electrotecnia (IEC), la Federación Internacional de Química Clínica y Biología Médica (IFCC), la ya mencionada Organización Internacional de Normalización (ISO), la Unión Internacional de Química Pura y Aplicada (IUPAC), la Unión Internacional de Física Pura y Aplicada (IUPAC) y la Organización Internacional de Metrología Legal (OIML). En 2005 se unió la Cooperación Internacional de Acreditación de Laboratorios (ILAC). Dichas instituciones mantienen activo un grupo de trabajo sobre la Guía para la Expresión de la Incertidumbre de Medida (GUM).
Evolución en el tratamiento de la incertidumbre de medida
La evolución en el tratamiento de la incertidumbre de medida, desde el enfoque del error hacia el enfoque de la incertidumbre, sigue una evolución lógica: medir, cometer errores, corregirlos, tener en cuenta esas correcciones o las incertidumbres de las propias correcciones y, finalmente, valorar la incertidumbre de la medida. Estos pasos son la secuencia adecuada para llegar a definir la calidad de la medición y, por tanto, también la calidad del resultado de la medida.
En el enfoque del error el objetivo de la medición es obtener una estimación del valor verdadero, inexistente en teoría, tan próxima a ese valor verdadero único como sea posible. Por otro lado, en el enfoque novedoso de la incertidumbre esta se manifiesta como un parámetro asociado con el resultado de una medida que caracteriza la dispersión de los valores que podrían, razonablemente, serle atribuidos (Prieto, 2011).
Diferencia entre error e incertidumbre
Es importante no confundir el término “error” con el concepto “incertidumbre”. Error es la diferencia entre el valor medido y el valor verdadero de la pieza que se mide, mientras que la incertidumbre es una cuantificación de la duda sobre el resultado de la medida. Es posible realizar correcciones para mitigar los efectos producidos por los errores conocidos, pero todos aquellos errores cuyo valor no se conoce constituyen una fuente de incertidumbre. Si el origen de los errores fuese conocido, la componente sistemática del error, el sesgo, podría ser corregido. Sin embargo, los errores al azar cambian de una determinación a otra y generan una duda cuantificable con la incertidumbre. De este modo, si la estimación de la incertidumbre de un procedimiento analítico o de un determinado tipo de muestra es conocida, se puede aplicar para todas las determinaciones, puesto que la incertidumbre no se puede corregir.
Importancia del concepto de incertidumbre en la medida
Uno de los aspectos interesantes del concepto de incertidumbre de medida es la posibilidad de aumentar la calidad de medida y ayudar a comprender su resultado. Cuando hay un margen de duda sobre una medida es necesario preguntar: ¿Cuán grande es el margen o intervalo? ¿Cuál es el nivel de confianza? ¿Cómo estamos de seguros de que el valor verdadero de la medida esté dentro del intervalo?
Además, tras el proceso de calibración de la incertidumbre de medida se debe indicar el certificado de calibración, que deberá ser correctamente comprendido e interpretado.
También a la hora de realizar un test se debe conocer la incertidumbre asociada para poder aplicar correctamente un determinado criterio de aceptación o rechazo. En la redacción de las especificaciones que debe cumplir un producto la incertidumbre asociada decide si el producto cumple los requisitos de calidad.
Para poder valorar la incertidumbre total hay que aislar y analizar cada componente para poder conocer su contribución. Cada una de esas contribuciones es un componente de la incertidumbre total y al expresarlo como desviación estándar se obtendrá la incertidumbre estándar. En caso de haber correlación entre los componentes, se tendría que tener en cuenta la covarianza.
Estadística básica aplicada al cálculo de incertidumbres
Hay un dicho muy empleado entre los sastres artesanos: “Medir tres veces, cortar una”. Esto nos viene a decir que es posible reducir el riesgo de cometer un error en el trabajo chequeando la medida que realizar una segunda vez y una tercera vez antes de proceder.
En efecto, es de sabios realizar una medida al menos tres veces, pues realizando solo una medida un determinado error podría pasar totalmente inadvertido. Empero, si se realizan solo dos medidas y estas no coinciden no podremos estar seguros de cuál de ellas es la correcta. Ahora bien, si realizamos tres medidas y dos de ellas coinciden entre sí mientras que la tercera es muy diferente, entonces podemos sospechar de la tercera.
Por tanto, se deben realizar al menos tres intentos para cualquier medición. La incertidumbre de medida no solo está ligada al error del operador, sino que hay otras buenas razones para repetir las medidas muchas veces. En consecuencia, se puede incrementar la información acerca de una medición tomando un número determinado de lecturas y aplicándoles luego unos cálculos básicos estadísticos para encontrar su valor promedio o media aritmética y su desviación estándar.
Si hay variaciones en las lecturas cuando estas se repiten, es mejor tomar varias lecturas y hallar su valor promedio. El valor promedio proporciona una estimación del valor verdadero. El valor promedio o media aritmética se muestra usualmente con un símbolo con una barra en la parte superior, en este artículo utilizaremos el símbolo µ para designar la media:
El término nindica el número de lecturas realizadas.
Cuanto mayor sea el número de lecturas realizadas mejor será la estimación del valor real de la medida. Empero lo ideal sería encontrar la media de un conjunto infinito de valores y, por tanto, lograr la mejor estimación de esta. En realidad, sería imposible efectuar un número infinito de medidas.
No se puede dar una recomendación general para el número de medidas que realizar, ya que este depende de las condiciones y exigencias de cada medición específica. En pocos casos se recomienda o se requiere un número mayor de 10; 10 medidas tomadas convenientemente son suficientes y simplifican los cálculos aritméticos. Usando 20 medidas solo obtendríamos una mejora muy sutil respecto a los resultados de las 10 medidas y emplear un número mayor de medidas, por ejemplo, 60 solo mejoraría muy levemente los resultados obtenidos con las 20 medidas a cambio de un esfuerzo realizado enorme para nuestros propósitos y el empleo de un tiempo excesivo.
Ejemplo de cálculo
Supongamos que como resultado de un proceso de medición se han realizado 10 lecturas, que son estas: 5, 9, 8, 6, 8, 7, 6, 8, 6 y 9. La suma total es 72 y el valor promedio de las 10 lecturas es µ= 72/10 = 7,2.
Debe calcularse la dispersión cuando se obtienen diferentes resultados al repetir la medida de un mismo parámetro. La dispersión de los valores proporciona información sobre la incertidumbre de medida. Conociendo la dispersión podemos valorar la calidad de la medida o la bondad del procedimiento utilizado para la realización de las medidas.
Algunas veces es suficiente conocer el intervalo entre el valor máximo y el mínimo. Pero la toma de pocos valores de medida puede ser insuficiente para tener información completa sobre la dispersión de las medidas en el intervalo considerado. Una dispersión grande podría producirse porque solo una de las medidas fuera muy diferente respecto de las otras.
Usualmente, para cuantificar la dispersión se utiliza la desviación estándar, que indica la diferencia entre las lecturas individuales y el valor medio de las lecturas.
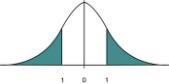
Hay que tener en cuenta que, aproximadamente, dos tercios de todas las lecturas tomadas en una medición caen dentro del intervalo determinado por ± la desviación estándar de la media, es decir, ± 1σ. Además, el 95% de todas las lecturas caerán dentro del intervalo de ± dos desviaciones estándar: ±2σ. En la figura 1 podemos ver la representación gráfica para la distribución gaussiana.
El valor verdadero de la desviación estándar solo puede obtenerse a partir de infinitas lecturas. Por tanto, a partir de un número limitado de lecturas solo será posible encontrar una estimación de la desviación estándar. La desviación estándar se calcula como:
Para el ejemplo anterior �n-1 = 1,398
Fuentes de incertidumbres
Muchas cosas pueden hacer que una medición tenga incertidumbre, y los defectos en la medición pueden ser visibles o invisibles, pues los procesos de medición reales nunca se realizan en perfectas condiciones y menos en entornos industriales. Podemos distinguir varios tipos de errores:
a) Errores asociados con el instrumento de medida utilizado. El instrumento de medida puede ser objeto de errores propios debido a cambios sufridos por envejecimiento, desgaste, deriva, escasa legibilidad, ruido eléctrico (para los instrumentos eléctricos), vibraciones y muchos otros problemas.
b) Errores relacionados con el dispositivo que está siendo medido. Pues puede que dicho dispositivo no sea estable.
c) Errores debidos al procedimiento de medición. Puede que el proceso de medición sea dificultoso de realizar.
d) Incertidumbres importadas. El instrumento con el que se van a realizar las medidas tiene que estar calibrado. La calibración del instrumento viene validada por su correspondiente certificado de calibración, en el que debe indicarse claramente la incertidumbre de uso del instrumento de medida. Esto no es ni más ni menos que la primera de las incertidumbres que considerar en el resultado de las medidas obtenidas en la práctica cuando se realice un proceso de medición.
e) Errores del operador. Algunos tipos de medición dependen en gran medida de la experiencia y habilidades del operador. Una persona puede ser mejor que otra a la hora de efectuar mediciones delicadas. Sin embargo, este tipo de errores no se suelen considerar en el cálculo de incertidumbres, pues se parte de la base de que el personal encargado de realizar las medidas tiene la experiencia y cualificación adecuadas.
f) Problemas de muestreo. El muestreo utilizado para la toma de medidas tiene que ser representativo de la magnitud que se quiere medir.
g) Errores debidos a las condiciones del entorno. La temperatura, la presión atmosférica, la humedad y muchas otras condiciones pueden afectar al instrumento de medida o al propio mensurando.
Cuando el tamaño y el efecto de un error son conocidos, como el resultado de una calibración, se puede aplicar una corrección determinada al resultado de la medida. No obstante, en general, las incertidumbres de cada una de estas fuentes, incluso de tantas otras, se consideran contribuciones de entrada que vienen a engrosar el conjunto total de las incertidumbres de la medida.
Generalización de los tipos de incertidumbres de medida y su representación
Las incertidumbres se pueden agrupar en dos tipos: aleatorias y sistemáticas.
– Aleatorias. Son aquellas que se producen cuando al repetir una misma medida varias veces los resultados son aleatoriamente distintos. Así pues, cuantas más medidas se tomen al calcular el valor medio mejor valor estimado del resultado de la medida se obtendrá.
– Sistemáticas. El resultado de la medida viene siempre acompañado del mismo error para cada muestreo repetitivo realizado. La repetición de las medidas no mejora en este caso el resultado final. Es necesario cuantificar el error sistemático o sesgo inherente a una medida determinada y o bien realizar un ajuste del instrumento para corregir el error sistemático o, si esto no es realizable, aplicar un valor de corrección.
La representación de la incertidumbre se realiza fácilmente haciendo uso de la función de distribución de probabilidad (PDF) de los resultados obtenidos al realizar las medidas.
Extensión de la incertidumbre
La extensión o diseminación de los valores obtenidos al realizar una medida puede tomar distintas formas que reciben el nombre de PDF. Una de las más comunes y utilizadas es la distribución normal o de Gauss (figura 1), caracterizada por su forma de campana al representar bidimensionalmente en el eje de ordenadas los valores de referencia y en el eje de abscisas los valores de las lecturas.
No son incertidumbres de medida:
– Los errores cometidos por los operadores. Estos no se deben contabilizar como contribuciones a la incertidumbre. Deben reducirse tratando de trabajar cuidadosamente y supervisando el trabajo realizado.
– Las tolerancias. Son límites de aceptación vinculados a unas determinadas especificaciones de un producto.
– Las especificaciones. Indican qué se puede esperar de un determinado producto, incluyendo cualidades no técnicas como la apariencia.
– La imprecisión. Imprecisión e incertidumbre no son sinónimos, aunque desafortunadamente la palabra precisión no se utiliza siempre adecuadamente. Hablando de forma correcta precisión es la proximidad entre las indicaciones o los valores obtenidos en mediciones repetidas de un mismo objeto, o de objetos similares, bajo condiciones especificadas, mientras que incertidumbre es un parámetro no negativo que caracteriza la dispersión de los valores atribuidos a un mensurando, a partir de la información utilizada (Prieto, 2011).
Cálculo de la incertidumbre de medida
Para calcular la incertidumbre de una medida deben identificarse en primer lugar las fuentes de incertidumbre en la medida que realizar.
Los tipos de incertidumbres enunciados en el apartado Fuentes de incertidumbre se suelen clasificar en dos grandes grupos: A y B. La evaluación tipo A de la incertidumbre es el método de cálculo de la incertidumbre mediante el análisis estadístico de una serie de observaciones. En este caso, la incertidumbre es la desviación experimental de la media que se deriva de un procedimiento promediado o de un análisis de regresión (CEM, 2010).
La evaluación tipo B de la incertidumbre es el método de evaluar la incertidumbre mediante un procedimiento distinto del análisis estadístico de una serie de observaciones. En este caso, la estimación de la incertidumbre se basa en otros conocimientos científicos. La influencia de cada componente sobre la incertidumbre no suele ser comparable. Por ello, a la hora de calcular la estimación total de la incertidumbre solo se tienen en consideración los componentes más influyentes (CEM, 2010).
Evaluación de incertidumbre tipo A
En la mayoría de los casos la repetición de n medidas dará como resultado una distribución de probabilidad normal o de Gauss. Entonces, la incertidumbre asociada viene dada por:
Incertidumbre tipo B
Se da cuando la información sobre los valores que pueda tener una variable es escasa y tan solo se puede estimar unos límites inferior y superior de incertidumbre. Es posible asumir que se distribuye uniformemente y aplicar los parámetros que aparecen en la tabla 1. O en otro caso utilizar una PDF particularizada según los casos.
Combinación de incertidumbres
La incertidumbre debe presentarse en forma de distribución estándar. Una vez calculadas las incertidumbres tipo A y tipo B, estas se combinan de una forma cuadrática y dan lugar a la incertidumbre estándar combinada u c.
En el caso de que entre las variables exista dependencia la expresión de la incertidumbre debe incluir la covarianza entre las variables dependientes.
Para el caso más sencillo en que los modelos o ecuaciones utilizadas solo tienen sumas y restas entre los distintos componentes, la incertidumbre total combinada se calcula mediante la expresión:
Esta forma sencilla de proceder con las incertidumbres parciales solo es posible si son independientes unas de otras. Si están correlacionadas, hacen falta cálculos adicionales y el problema se complica más cuanto mayor sea el número de incertidumbres parciales que hay que considerar.
En la tabla 2 se exponen las distintas expresiones para el cálculo de la incertidumbre combinada según las operaciones matemáticas implicadas en la función modelo utilizada para el cálculo de incertidumbres de una determinada magnitud medida. En los casilleros con (*) el resultado de estos cálculos es la incertidumbre combinada relativa. Para calcular en estos casos la incertidumbre combinada absoluta hay que multiplicar el resultado aquí obtenido por la mejor aproximación del mensurando.
Incertidumbre expandida
Es norma, al emitir un certificado de calibración, expresar la incertidumbre de forma expandida a un cierto intervalo de nivel de confianza según la PDF adoptada como respuesta de la magnitud medida.
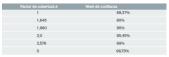
Para evaluar la incertidumbre expandida, es necesario seleccionar el factor de cobertura k. Este factor puede seleccionarse de acuerdo al tipo de distribución. Así, para la distribución normal de la figura 1, el 95% de cobertura se calcula con k = 1,96 o mejor por conveniencia k = 2, lo que da el 95,45% de nivel de confianza, como indica la tabla 3.
En general, cuando se da la incertidumbre expandida, se selecciona el valor de 2 asumiendo que los resultados siguen una distribución normal al 95,5% de nivel de confianza. No obstante, cualquier valor del factor de cobertura k seleccionado se debe declarar cuando se reportan las incertidumbres expandidas.
Una forma más rigurosa de seleccionar k es mediante la evaluación de los grados efectivos de libertad de la incertidumbre total combinada, utilizando la conocida expresión de Welch-Satterthwaite (Fluke, 2011).
En donde: uef. son los grados efectivos de libertad para la incertidumbre combinada uc. Uc. es la incertidumbre combinada.
u. es cada una de las incertidumbres a considerar.
ci. es cada uno de los coeficientes de sensibilidad
vi. son grados de libertad de cada incertidumbre u considerada.
De este modo, una vez obtenidos los grados efectivos de libertad vef. utilizamos para evaluar la incertidumbre expandida, un factor de cobertura k que nos garantice un nivel de confianza del 95%. Para ello, con los grados efectivos de libertad obtenidos a partir de la expresión de Welch-Satterthwaite se entra en la primera columna de la tabla 4 y en la columna correspondiente al 95% se obtiene el valor del factor de cobertura k requerido.
Considerando una distribución normal la de la figura 1, la incertidumbre combinada corresponde a una desviación estándar con un nivel de confianza del 68%. Si se desea elevarla a otro nivel de confianza, por ejemplo del 95%, debe utilizarse una incertidumbre combinada correspondiente a dos desviaciones estándar. Por lo que la incertidumbre combinada hay que multiplicarla por dos. De este modo, el producto del factor de cobertura por la incertidumbre combinada proporcionará en cada caso la incertidumbre expandida U (CEA-ENAC, 1998).
U expandida = k uc
El valor particular del factor de cobertura corresponde a un valor particular del nivel de confianza de la incertidumbre expandida. Para otro tipo de funciones de distribución el factor de cobertura será distinto. Y distinto también según el intervalo de confianza requerido como lo indica la tabla 2.
Ejemplo de la estimación de la incertidumbre en la calibración
Caso de un calibrador o pie de rey
Para determinar la incertidumbre del calibrador o pie de rey de la figura 2, con resolución 0,02 mm e intervalo de medición de 0 a 150 mm, consideraremos como contribuciones a la incertidumbre las siguientes:
Tipo A:
– Incertidumbre por repetitividad
(u1). Tipo B:
– Incertidumbre por resolución del calibrador (u2).
– Incertidumbre del patrón utilizado (u0).
– Incertidumbre por error de Abbe (u3).
– Incertidumbre por efectos térmicos (u4).
Para el cálculo de la u1 se estima la desviación estándar de la media a partir de n mediciones repetidas en un punto. El cálculo se repite en cada punto donde se calibre el instrumento, tomándose el mayor de todos.
Suponemos que la desviación estándar más elevada se presenta a los 150 mm y que las 10 lecturas dan una desviación de 0,019 mm y consideramos que la distribución es normal:
En el caso de la incertidumbre por resolución del calibrador u2, esta queda determinada por la mínima división del instrumento. Además se supone una distribución uniforme:
Como de alguna manera la resolución del instrumento participa en el resultado de las medidas obtenidas en el apartado de repetitividad para la evaluación de u1, y siendo u2 menor que u1, tomamos solo la mayor u1. Es decir, en el balance de incertidumbres se toma en cuenta el valor más grande entre repetibilidad y resolución.
En lo referente a la incertidumbre del patrón de referencia u0, en este caso es el maestro de longitudes fijas. Es un caso típico de calibración contra valores nominales, que implica no aplicar ninguna corrección del certificado de calibración del patrón, donde se expresa la incertidumbre expandida como:
U patrón= 2 u estándar del patrón
De modo que:
u0 = Desviación máxima + u estándar del patrón
La desviación máxima del patrón es la correspondiente dentro del intervalo de medición del instrumento por calibrar. También se obtiene del informe de calibración. Para este ejemplo: u0 = 2 µm
Error de Abbe
Ernst Carl Abbe fue un científico alemán que a finales del siglo XIX desarrolló junto con Carl Zeiss y Otto Schott las bases de la óptica moderna. Uno de los errores descubiertos en sus investigaciones sobre la fabricación de instrumentos de precisión es el debido al llamado principio del comparador de Abbe, de modo que el incumplimiento de este principio produce lo que se conoce como error de Abbe.
El principio del comparador de Abbe establece que la longitud que se trata de medir y la normal de comparación, por ejemplo el husillo de un micrómetro, deben estar dispuestos continuamente y en línea recta. El pie de rey no cumple el principio del comparador de Abbe. Esto es porque aunque la longitud que medir y la escala de la regla graduada sean paralelas, no están alineadas una tras la otra, sino una debajo o encima de la otra (v. figura 2). Por tanto, se debe considerar esta contribución a la incertidumbre del instrumento.
Entonces la incertidumbre debida al error de Abbe es un valor tipificado para este tipo de instrumentos resultando ser:
Donde h es la altura de la mordaza de medición, que es de 40 mm tomada al extremo de las puntas de medición. Como se está realizando una calibración y, en consecuencia, se trata de disminuir al mínimo los errores, se colocan las puntas de medición lo más al fondo posible, de manera que se tiene para h un valor de 20 mm.
El valor a representa el juego entre el cuerpo del calibrador y el cursor, que es de 0,01 mm, mientras que L representa la longitud del cursor de 53 mm.
Considerando que la calibración se realiza en un entorno con temperatura controlada, despreciamos las incertidumbres debidas a los efectos térmicos, por lo que u4 = 0.
La incertidumbre estándar combinada uc viene dada entonces por la siguiente expresión:
Considerando que al tomar 10 medidas se obtienen nueve grados de libertad, es posible considerar la incertidumbre expandida un factor de cobertura k = 2 para un intervalo de confianza del 95% suponiendo distribución normal. Por ello:
U expandida = 2 · 6,7 = 13,4 µm. Que podemos redondear a 14 µm. Por lo que:
U exp = ± 14 µm
Caso de un multímetro digital de 3,5 dígitos
La calibración la realizamos para 10 amperios en corriente alterna a 50 hercios. Realizamos cuatro medidas independientes, que nos dan como resultado: Media= µ = 10,05 A
Desviación = � = 0,02836 A = 28,4 mA
Suponemos PDF normal, por lo que:
Coeficiente de sensibilidad
El coeficiente de sensibilidad asociado a la estimación de entrada describe el grado en que la estimación de salida se ve afectada por variaciones en la estimación de entrada (CEM, 2010). Pondera, por tanto, lo que cada una de las distintas fuentes de incertidumbre pesa sobre la incertidumbre final de la magnitud medida (CEA-ENAC, 1998). Se puede evaluar a partir de la función modelo que describe el proceso de medición y que representa la respuesta del mensurando, a partir de la siguiente expresión, que es para el caso de medidas directas con un calibrador igual a la unidad.
Coeficiente cambio de la respuesta del mensurado de= = 1 sensibilidad cambio en el estímulo
Grados de libertad = N-1 = 4-1 = 3
El calibrador utilizado tiene una incertidumbre en sus especificaciones dada y suponiendo PDF rectangular tenemos:
Coeficiente cambio de la respuesta del mensurado de= = 1 sensibilidad cambio en el estímulo
Grados de libertad = ∞
La incertidumbre u3 debida a la resolución del instrumento se calcula considerando que para 10 A la resolución del instrumento es de 10 mA, por lo que:
Suponemos PDF rectangular
Coeficiente de sensibilidad = 1
Grados de libertad = ∞
Como u3 es menor que u1, tomamos solo u1. Además, al no utilizar posteriormente corrección alguna, consideramos la incertidumbre u4 de la desviación al nominal.
PDF rectangular
Coeficiente de sensibilidad = 1
Grados de libertad = 3
Considerando que la calibración se realiza en un entorno con temperatura controlada, despreciamos las incertidumbres debidas a los efectos térmicos. La incertidumbre combinada es, por tanto:
Los grados efectivos de libertad los obtenemos por aplicación de la expresión de Welch-Satterthwaite.
De la tabla 4 correspondiente a la distribución t para dos colas, vemos que para 4 grados de libertad y un nivel de confianza del 95% corresponde un factor de cobertura k = 2,78. Por ello, la incertidumbre expandida es:
U exp=ku c = 2,78 ·32,33 ≈ ± 90 mA
El valor final de la medida incluyendo las incertidumbres para este valor calibrado es:
I = µ ± U expandida= 10,05 ± 0,09 amperios
A un nivel de confianza del 95% con distribución normal.
Método de Montecarlo
El método de Montecarlo (MMC) es una técnica numérica para calcular probabilidades y otras cantidades relacionadas utilizando secuencias de números aleatorios, en contraposición con la GUM, que utiliza métodos deterministas de estadística clásica para la evaluación de incertidumbres tipo A, evaluando incertidumbres tipo B y sus combinaciones por medio del método bayesiano de soluciones analíticas (CEM, 2010).
Es, por tanto, el MMC un método estocástico que utiliza una secuencia de estados cuya evaluación viene determinada por sucesos al azar, en los que las relaciones causa-efecto no explican la evolución de un sistema de manera determinista, sino en función de probabilidades.
El término “método Montecarlo” fue acuñado en 1949 por Stanislaw Marcin Ulam y Nicholas Constantine Metropolis en referencia al principado de Mónaco, por ser esta la capital del juego de azar, al tomar una ruleta como un generador simple de números aleatorios.
El MMC se convierte en una alternativa práctica a la GUM cuando:
– La linealización del modelo del mensurando provee una representación poco adecuada.
– La PDF para el mensurando se aparta de una distribución gaussiana o de una distribución t escalada y sesgada, debido a asimetrías.
– Se necesita validar los resultados obtenidos por el método de la GUM, ante procesos de acreditación según ISO/IEC 17025, valoraciones de aptitud e intercomparaciones entre laboratorios.
El MMC permite combinar por simulación numérica probabilística las PDF de las magnitudes de entrada y obtener la PDF del mensurando con PDF no necesariamente normal o t como presupone la GUM. Se evitan cálculos con derivadas parciales y cálculos de los grados efectivos de libertad por aplicación de la ecuación clásica de Welch-Satterthwaite.
El MMC resulta una forma cómoda para determinar el cumplimiento del “teorema central del límite” ante determinadas situaciones. El teorema central del límite o mejor el teorema del límite central, ya que central califica al límite más que al teorema, garantiza una distribución normal cuando el número de repeticiones es suficientemente grande. Establece que es suficiente que las variables que se suman sean independientes, idénticamente distribuidas, con valor esperado y varianza finitas (Blaiotta, 2004). Con todo, acreditados analistas enuncian que la PDF normal o de Gauss es, en la práctica, la PDF menos normal (Méndez, 2010). Con el MMC esto se puede comprobar fácilmente después de realizar un número lo suficientemente elevado de iteraciones como se ilustra a continuación en este artículo con un sencillo ejemplo.
Operatoria del MMC
Para el caso de una sola variable el procedimiento es el siguiente:
– Generar una serie de números aleatorios, r1, r2,…, rm, uniformemente distribuidos en [0,1].
– Usar esta secuencia para producir otra secuencia, x1, x2,…, xm, distribuida de acuerdo a la PDF en la que estamos
interesados.
– Usar la secuencia de valores x para
estimar alguna propiedad de f(x). Los
valores de x pueden tratarse como medidas
simuladas y a partir de ellos puede
estimarse la probabilidad de que las x
tomen valores en una cierta region.
Formalmente, un calculo MMC no es
otra cosa que una integracion y el MMC
es muy util para integraciones multidimensionales.
Precision del MMC
La precision del MMC se define, aproximadamente,
como =1/Vn, en el que n
es el numero de valores aleatorios generados.
Si comparamos con otros metodos
de integracion numerica como el
metodo trapezoidal (metodo de integracion
numerica) tiene una precision de,
aproximadamente, =1/n2. Cuando el
numero de valores es alto como en el caso
multidimensional con d dimensiones,
la precision del MMC es independiente
de d (siempre =1/Vn) mientras que, por
ejemplo, la del metodo trapezoidal tiene
una precision de, aproximadamente,
=1/n2/d siendo dependiente del numero
de dimensiones. Por eso para el caso multidimensional
(d > 4 tipicamente) con
multiples variables de entrada, el MMC
da la mayor precision.
Precision MMC =1/Vn (independiente
del numero de dimensiones)
Su convergencia es proporcional a Vn
y su error es decreciente conforme
aumenta el numero de iteraciones.
‘Software’ para implementar el MMC
Existe una amplia variedad de programas Tabla 6. Aplicación del MMC a una función de seis variables. científicos y comerciales desarrollados para realizar funciones matemáticas y Tabla 7. Generación de PDF trapezoidal por el MMC. estadísticas para el análisis de datos como: Matlab, Maple, Labview, Microsoft Excel, Lotus, etc. Para los cálculos que se presentan a continuación se ha utilizado el programa comercial Microsoft Excel, ya que está ampliamente difundido y, además, tiene una gran cantidad de funciones disponibles sin necesidad de programación, con lo que se logran resultados rápidamente. Además, cuenta con herramientas tales como: análisis de datos, auditoría de fórmulas y funciones definidas por el usuario. También permite programación mediante: grabación de macros, edición de macros en VBA (Visual Basic for Applications) y demás.
Las funciones para desarrollar el MMC con Excel son:
– Generación de números aleatorios de diferentes tipos de PDF con Herramientas > Análisis de datos > Generación de números aleatorios. O bien utilizando la función ALEATORIO (), que genera números aleatorios entre 0 y 1 con una PDF uniforme con la función ALEATORIO.ENTRE (). Y en lenguaje de Visual Basic con la función RND, que es la abreviatura de random.
- – Calcular intervalos de cobertura para cierto nivel de confianza con la opción:
Función PERCENTIL (matriz; k), que permite establecer un umbral de aceptación. Es adecuada para cualquier PDF resultante del mensurando.
Ejemplos de aplicación del método de Montecarlo
En la tabla 5 se reproduce el resultado gráfico de la aplicación del MMC para el caso de tres variables, dos de ellas con PDF uniforme y una tercera con PDF normal, correspondiente al ejemplo anterior del pie de rey resuelto aplicando los criterios de la GUM. Como se ve el resultado o valor del mensurando para este sencillo caso sigue una PDF normal como lo muestra la gráfica obtenida aplicando el MMC con 10.000 repeticiones.
El número de variables de entrada aumenta como en el caso de la tabla 6, en la que se ha representado la aplicación del MMC a la determinación de un volumen V, cuyo valor depende de seis variables, cuatro de ellas con PDF normal y otras dos con PDF uniforme.
El valor resultante del mensurando no tiene por qué cumplir el teorema del límite central. Como lo muestra la PDF obtenida al aplicar el MMC con 10.000 iteraciones utilizando una macro del tipo:
Sub volume ()
Dim i As Long
For i=1 To 10000
Cells (i, “H”) = Range (“D1”). Value Next i
End Sub
Obtenemos el resultado de la tabla 7. El valor del mensurando distribuido con una PDF se aleja de ser normal o de Gauss en contra de lo predicho por el teorema del límite central. Por ello, para este caso el factor de cobertura para el 95% de nivel de confianza será distinto de dos.
Generación de PDF con el método de Montecarlo
Con el MMC se pueden simular distintas funciones de densidad de probabilidad. Por ejemplo, la representada en la tabla 7, en la que se muestra el resultado obtenido al simular una PDF trapezoidal.
Hay dos caminos para obtener una PDF trapezoidal aplicando el MMC:
– Usar el método de la función inversa.
– Generar y sumar dos distribuciones uniformes.
Empleando el segundo camino, a partir de la generación de dos PDF uniformes o rectangulares y su posterior suma se ha obtenido la representación mostrada en la tabla 7. Aunque al simular por MMC se han realizado 1.000.000 de iteraciones con la ayuda de una macro generada al efecto, los resultados permanecen estables a partir de las 200 y 1.000 iteraciones. Esto es porque el valor de la media y desviación estándar se estacionan a medida que aumenta la cantidad de iteraciones. El número de iteraciones al ocupar estas filas de la hoja de cálculo Excel se vería limitado a 16.384 en Excel 97, a 65.536 en Excel 2003 y solo en Excel 2010 llegaríamos a 1.048.576 iteraciones posibles. Esto se debe a que al generar las iteraciones con una macro esta no permite trabajar con distintas hojas de cálculo que lleven datos de variables, sí se puede para trabajar con datos de texto.
Se podrían generar de esta forma comportamientos de variables de medida a partir de la combinación de variables de entrada con distintas PDF: uniforme, uniforme y normal o uniforme, normal y triangular, etc.
Bibliografía
BIPM (1995). Guide to the expression of uncertainty in measurement.
Blaiotta J, Delieutraz P. Facultad de Ciencias Exactas (2004). Teorema central del límite. Disponible en: http://www.u-cursos.cl/ingeniería (consultado en julio de 2012).
CEA-ENAC-LC/02 (enero 1998). Expresión de la incertidumbre de medida en las calibraciones. Rev. 1.
CEM (2010). Evaluación de Datos de Medición. Suplemento 1 de la GUM.
Fluke Calibration (2011). Basics of Measurement Uncertainty for DMM Calibration.
Guía EA-4/02 (2004). Expression of the uncertainly, calibration and probability. Segunda edición.
International Standard ISO/IEC 17025 (1999). General Requirements for the competence of testing and calibration laboratories. 1ª edición.
Méndez Arias J, Ramírez Varas L (2010). Validación de la estimación de incertidumbre en la calibración de matraces para el método de sustitución simple sin masa de sensibilidad mediante el Método de Monte Carlo. San José, Costa Rica.
Muñoz Bueno R. LMM-ETSII-UPM. (Curso académico 2011-12). Introducción a la Metrología.
Pachón Veira R F, Manzano Agugliaro, F XIV Congreso Internacional de Ingeniería Gráfica. Santander (junio 2002). Metrología en las Civilizaciones de Mesopotamia, Egipto, Fenicia, Israel, Grecia, Cartago, Roma y otras culturas de la Antigüedad.
Prieto Esteban E, Del Campo Maldonado M D. Jornada CEM-AENOR (2011). Normalización en la expresión de la calidad de la medida.
Ríos S (1972). Análisis estadístico aplicado. Paraninfo. Madrid. ISBN: 8428304688.
Wittwer J. W. (2004). Monte Carlo Simulation in Excel.
– Programar diferentes funciones inversas de probabilidad generando la probabilidad seudoaleatoria a partir de la función ALEATORIO() como: DISTR.NORM.INV (ALEATORIO (); media; desviación estándar) DISTR.T.INV (ALEATORIO (); grados de libertad) DISTR.LOG.INV (ALEATORIO (); media; desviación estándar)
– Posibilidad de graficar histogramas y PDF con: Herramientas > Análisis de datos…> Histogramas, o utilizando la función FRECUENCIA (datos; grupos).