Diseño de un estimador basado en redes neuronales artificiales para caracterizar la frenada de un vehículo

María Garrosa (1), Ester Olmeda (1), Susana Sanz Sánchez (1), Vicente Díaz (1)

Resumen
Hoy en día, los vehículos inteligentes están equipados con interfaces de usuario muy avanzadas que pueden reaccionar ante las decisiones y necesidades del conductor. De esta manera mejora la dinámica vehicular según la situación de conducción evitando posibles colisiones fortuitas. Esta tecnología permite tomar decisiones sobre la conducción con un nivel de resolución superior al humano a la hora de, por ejemplo, realizar una frenada de emergencia ante un imprevisto. Con este trabajo se pretende que, en un futuro, se pueda gobernar el sistema de frenado de manera automática y que el vehículo pueda reproducir los hábitos y las formas de actuación de los conductores durante la maniobra de frenada de un vehículo, pero corrigiendo los posibles fallos humanos ligados a distracciones, falta de visibilidad y tiempos de reacción. Un sistema de frenado inteligente ha de ser capaz de obtener información de los diferentes sensores embarcados en el vehículo, procesar los datos obtenidos a través de los mismos y transformarlos en información útil para el control activo del automóvil. Con el vehículo instrumentado con los sensores capaces de proporcionar en tiempo real información sobre el sistema de frenado se llevan a cabo una serie de ensayos. Los datos obtenidos experimentalmente durante la realización de los ensayos se utilizan para el diseño de un estimador mediante la técnica de redes neuronales artificiales. Se estimarán las variables medidas por los sensores con el fin de caracterizar una frenada.

Palabras clave:  Sensor de presión, redes neuronales artificiales, estimación de la presión del sistema de frenado

Abstract
Today, smart vehicles are equipped with highly advanced user interfaces that can react to the driver’s decisions and needs. In this way, it improves vehicle dynamics according to the driving situation and avoiding possible accidental collisions. This technology makes it possible to make decisions about driving with a level of resolution higher than human, for example, carrying out an emergency braking in the event of an unforeseen event. With this work it is intended that, in the future, the braking system can be governed automatically and that the vehicle can reproduce drivers’ habits and forms of action during the braking maneuver of a vehicle, but correcting the possible human failures linked to distractions, lack of visibility and reaction times. An intelligent braking system must be able to obtain information from the different sensors on board the vehicle, process the data obtained through them and transform them into useful information for the active control of the car. With the vehicle instrumented with sensors capable of providing real-time information about the braking system, a series of tests are carried out. The data obtained experimentally during the tests are used to design an estimator using the artificial neural network technique. The variables measured by the sensors will be estimated in order to characterize a braking.

Keywords: Pressure sensor, artificial neural network, brake pressure estimation

---

Recibido / received: 16/06/2021. Aceptado / accepted: 24/10/2021.

1 Instituto de Seguridad de los Vehículos Automóviles Duque de Santomauro (ISVA), Departamento de Ingeniería Mecánica, Universidad Carlos III de Madrid.

Correspondencia: mgarrosa@ing.uc3m.es, eolmeda@ing.uc3m.es, ssanz@ing.uc3m.es, vdiaz@ing.uc3m.es

Doi: 10.23800/10515

---

Introducción
A lo largo de las últimas décadas se han sucedido avances de gran importancia en los sistemas de seguridad de los automóviles, tanto activa como pasiva. A partir de que apareciera, a comienzos de la década de 1970, el sistema antibloqueo de frenos (ABS – Antilock Brake System), que fue el primer sistema de asistencia al conductor, han surgido nuevos medios que ayudan a disminuir la probabilidad de tener un accidente o disminuyen sus consecuencias en caso de que se produzca. Dentro de estos mecanismos de ayuda se engloban las técnicas de control de estabilidad, frenado automático, control de crucero adaptativo, control de descenso en pendientes y los sistemas de tracción. En todos estos ejemplos se requiere de sensores embarcados en el vehículo, procedimientos para estimar las variables, algoritmos de control y componentes que actúen en función de la salida de los mismos, para que puedan llevarse a cabo las tareas para las cuales han sido concebidos. El equipo de seguridad activa más importante en los automóviles es el sistema de frenado, y es un aspecto fundamental en la dinámica de los mismos. Hay multitud de investigaciones orientadas a mejorar el sistema de frenado de un vehículo. En Park et al. [1] se implementa un controlador de deslizamiento de rueda en un sistema de frenos magnetoreológico. El sistema de frenos propuesto basa su funcionamiento en dos discos giratorios sumergidos en un fluido magnetoreológico y rodeados por un electroimán. En este sistema de frenos la tensión de fluencia del fluido, que es la que produce la fricción en las superficies de los discos giratorios, varía en función del campo magnético aplicado por el electroimán. En base a esto, en este estudio se controla el par de frenado con precisión cambiando la corriente que se aplica al electroimán. D’alfio et al. [2] proponen un sistema de frenado inteligente utilizando discos de freno denominados “de contacto total” y servoválvulas. Se busca con ello conseguir el máximo rendimiento reemplazando las pastilla por discos completos, controlando así los frenos de manera continua y no cíclicamente como ocurre en los sistemas clásicos de ABS. Para proporcionar un mejor control, el regulador utiliza información de retroalimentación no solo del deslizamiento, sino también del par de frenado. Castillo et al. [3] desarrollanuna arquitectura de frenado basada en el control continuo de la presión de frenado haciendo uso de servoválvulas proporcionales. El algoritmo de control emplea las técnicas de filtro de Kalman extendido para la estimación de los parámetros de frenado: esfuerzos en el neumático, coeficientes de adherencia y velocidad, gracias a los valores obtenidos con los sensores embarcados en el vehículo automóvil. Mediante el uso de redes neuronales artificiales se estima el deslizamiento óptimo y, por último, se utilizan bloques difusos optimizados con la ayuda de algoritmos genéticos para poder establecer la presión apropiada en el sistema de frenado. Doumiati et al. [4] proponen, para el cálculo de las fuerzas laterales de los neumáticos y el ángulo de deslizamiento lateral, algoritmos de estimación basados en filtros de Kalman extendido y “unscented”. Doumiati et al [5] estiman las fuerzas que aparecen en el contacto neumático-calzada por medio de observadores que se basan en filtros de Kalman. Shraim et al [6] calculan las fuerzas en el contacto neumático-calzada, velocidad angular de las ruedas, velocidad del vehículo y el ángulo de deslizamiento lateral del vehículo con la ayuda de observadores en modo deslizante a partir de las medidas de: ángulo de dirección, ángulo de deriva, par aplicado en cada rueda y velocidad de guiñada.

En el presente artículo se instrumenta un vehículo automóvil con distintos sensores capaces de proporcionar información útil del sistema de frenado en tiempo real. Para la adquisición de los datos que proporcionan los distintos sensores se ha llevado a cabo una serie de ensayos experimentales. Estos consisten en frenar un vehículo a distintas velocidades sobre una pista de suelo plano siguiendo una trayectoria recta. La investigación se centra en el diseño de un sistema de estimación basado en redes neuronales artificiales (RNA) que pronostique el comportamiento de los sensores de presión incorporados en el circuito hidráulico de frenos en función de las condiciones de contorno presentes en la maniobra de frenada. El sistema ha de ser capaz de simular los valores reales recogidos por los sensores con el fin de caracterizar la frenada de un vehículo y ser utilizado en condiciones reales de circulación. El estimador utilizará como datos de entrada la velocidad del vehículo y el espacio de frenado y buscará, como respuesta del sistema estimador, la presión que debe sufrir el sistema de frenado.

Metodología de ensayo
En este apartado se explica la metodología que se ha seguido para el adecuado desarrollo de la fase experimental, así como la instrumentación utilizada en ella. Se va a detallar el procedimiento seguido en la ejecución de los ensayos dinámicos y las condiciones de contorno de estos.

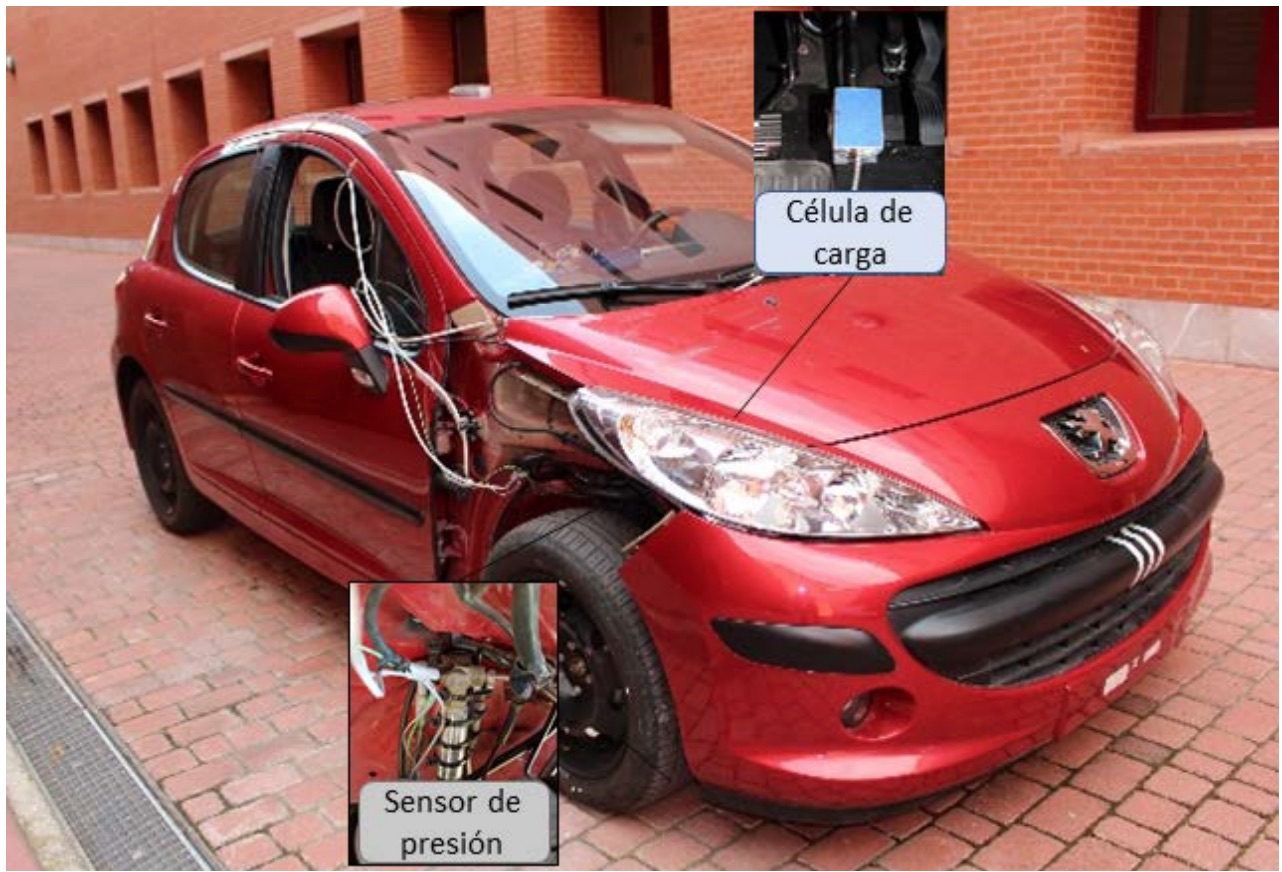
Vehículo instrumentado
El vehículo que se ha utilizado para la realización de los ensayos experimentales es un turismo comercial Peugeot 207 1.6 HDI 16 v (Fig. 1). El dispositivo de frenado de servicio es hidráulico a las cuatro ruedas con dos circuitos independientes (tipo X). Utiliza freno de disco en ambos ejes y cuenta con sistemas de asistencia ABS y ESP.

Se describen a continuación los sensores embarcados en el vehículo a fin de obtener los parámetros dinámicos requeridos:

• Sensores de presión incorporados en el circuito de frenos. Para determinar la capacidad de frenada del sistema se estudia la presión en el circuito de frenos, tomando esta como indicativo de la misma. Con el objetivo de conocer la presión instantánea durante los ensayos, se ha equipado el sistema de frenos con dos transductores de presión extensométricos. Los sensores son de tipo PDCR 911, de la marca DRUCK LIMITED y poseen un rango de operación de 0 a 135 bares. El control de la presión en el circuito de frenos es un indicador para determinar en qué momento se debe limitar la presión del circuito, como medio de alteración de la capacidad de frenada del vehículo. Con objeto de medir la presión lo más cerca posible al sistema pinza-disco, se instalan los sensores de presión entre la entrada de la pinza de freno y el último tramo del circuito hidráulico de frenos (Fig. 2).

• Célula de carga incorporada en el pedal de freno. Se ha empleado una célula de carga ubicada sobre el propio pedal de freno para conocer con exactitud el momento en el que el conductor empieza a frenar. En la figura 3 se muestra el montaje del sensor HKM PK 2.0 sobre el pedal de freno.

· Equipo de adquisición de datos. El equipo de adquisición de datos utilizado en la fase experimental es el VBOX 3i Dual Antenna. Conectadas al módulo principal se incorporan dos antenas gemelas orientadas longitudinalmente sobre el techo del vehículo (Fig. 4). La antena principal proporciona los valores de tiempo, velocidad y posición a través del efecto Doppler en la señal portadora de GPS.

Una conexión de bus CAN se conecta a DATA 1 del módulo externo VBOX Mini Input. En las entradas analógicas del módulo externo se conectan la célula de carga instalada sobre el pedal de freno y los sensores de presión (Fig. 5).

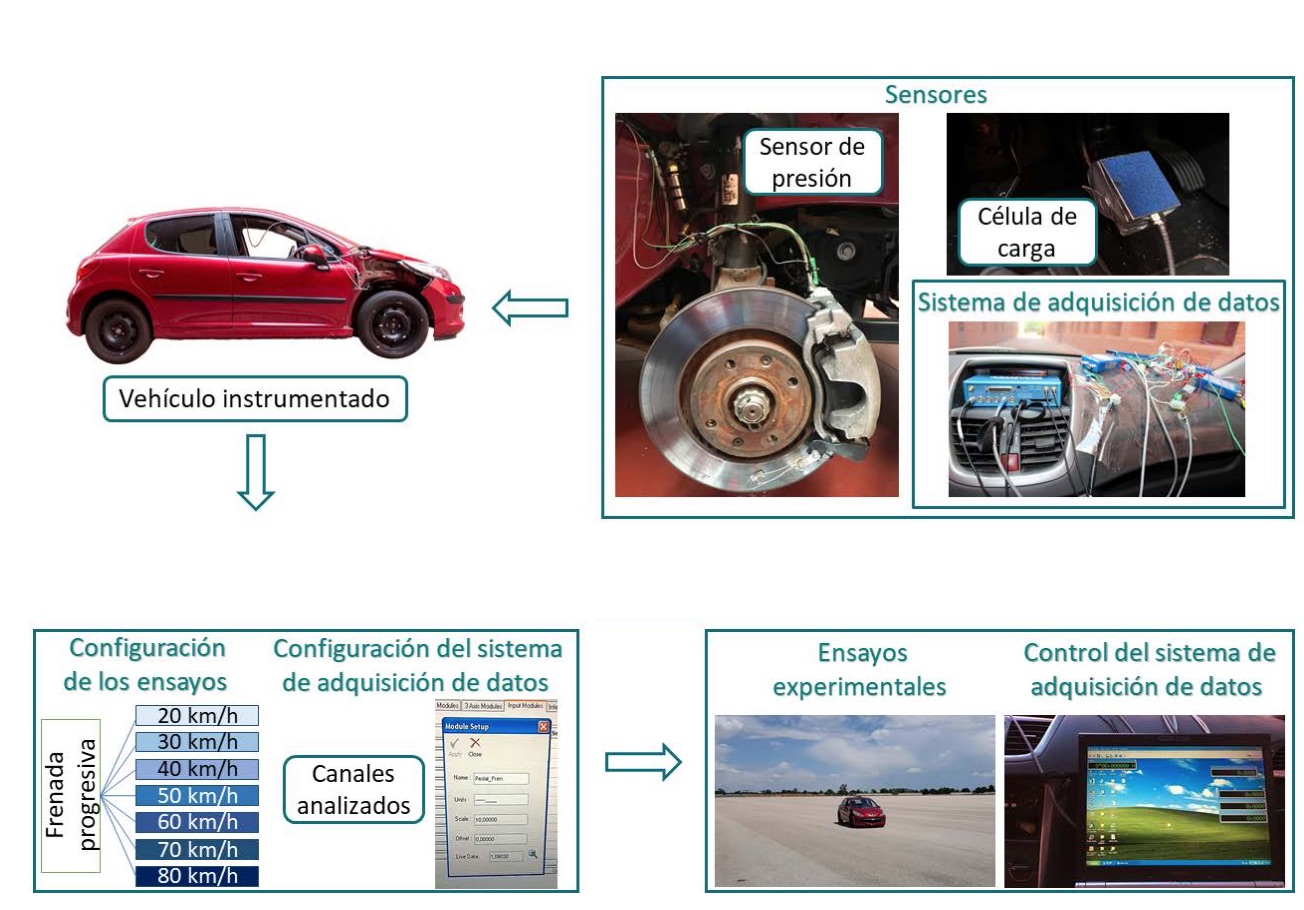
Metodología de la fase experimental
Todos los ensayos se han realizado en las mismas condiciones de pista y adecuación del vehículo. Sobre suelo plano, uniforme y seco el conductor ha efectuado, siguiendo una trayectoria rectilínea, una serie de frenadas con el vehículo hasta detenerlo. El rango de velocidades estudiado está comprendido entre 20 y 80 km/h, incrementando la velocidad en intervalos de 10 km/h.

En la realización de los ensayos experimentales han participado 14 conductores, todos hombres con una edad comprendida entre 22 y 30 años.

Una vez alcanzada la velocidad de ensayo, el conductor ejecuta la frenada de manera progresiva, es decir, en un primer momento se aplica una presión suave sobre el pedal de freno y, progresivamente, se aumenta la presión hasta que el vehículo se detiene. Este es el tipo de frenada que se realiza habitualmente en la conducción de un vehículo. En la figura 6 se muestra de manera esquemática el diagrama de flujo para la adquisición de los datos de la fase experimental.

Variables analizadas en los ensayos en pista
En los siguientes puntos se enumeran y explican de manera concisa las variables que se han medido durante la realización de los ensayos experimentales en pista:

• Tiempo de frenado. El tiempo de frenado que se ha considerado en este trabajo es el comprendido desde que el conductor presiona el pedal de freno hasta que el vehículo se detiene completamente. No se ha evaluado el tiempo de reacción del conductor ni el tiempo que emplea para levantar el pie del pedal de freno, ya que la realización de la frenada es premeditada y pueden obviarse dichos términos. La célula de carga instalada en el pedal de freno es el trigger de inicio del tiempo de frenado. De esta manera permite conocer con exactitud el momento en el que el conductor empieza a aplicar la fuerza sobre el pedal de freno. El GPS será el encargado de poner fin al tiempo de frenado en el momento en el que se registre una velocidad igual a cero.

• Distancia de frenado. La distancia de frenado será la distancia total recorrida durante el tiempo de frenado, es decir, desde que el conductor presiona el pedal de freno hasta que el vehículo se detiene completamente. Este valor se deduce gracias al posicionamiento GPS del vehículo.

• Presión en el circuito hidráulico de frenos. Mediante los sensores de presión incorporados en el último tramo del circuito hidráulico, cerca de la pinza de freno, se consigue medir la presión en el sistema hidráulico.

Condiciones de ensayo
Para asegurar la repetitividad de los ensayos realizados, se han tenido en cuenta las siguientes condiciones de contorno:

• Los ensayos se han realizado con los neumáticos fríos y se ha controlado mediante un manómetro que la presión de inflado sea la óptima según las prescripciones del fabricante.

• La temperatura en el disco de freno, al inicio de un conjunto de ensayos para todo el rango de velocidades estudiado, ha de estar comprendida en el intervalo 18-31 ºC. Una vez finalizadas las siete frenadas consecutivas se ha esperado a que el disco se enfríe a temperatura ambiente. Para conocer la temperatura en el disco de freno se ha utilizado un termopar tipo K.

• Además del conductor, en todos los ensayos, ha habido una segunda persona en el asiento del copiloto encargada de controlar el sistema de adquisición de datos y supervisar las condiciones de ensayo.

• Todos los ensayos se han realizado con el motor desembragado para que los conductores no se apoyen en el freno motor y así evitar que la fuerza de retención del motor se sume a la capacidad de frenada.

Análisis de resultados

Lectura directa de los sensores
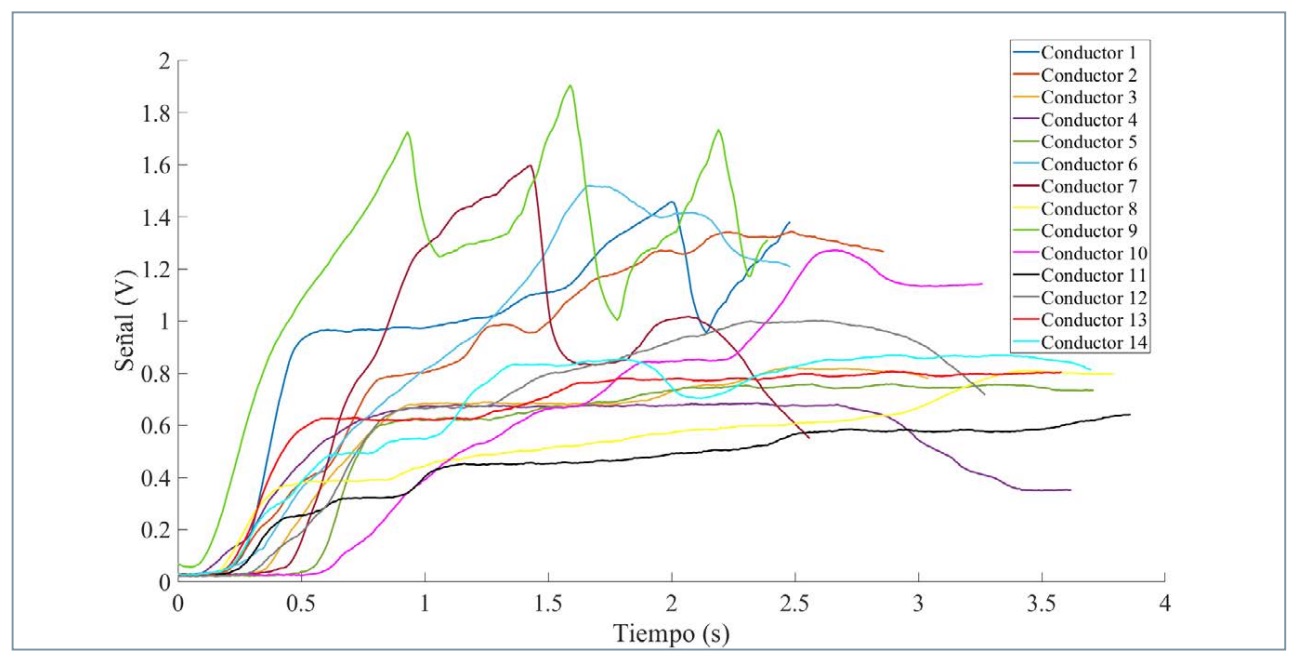
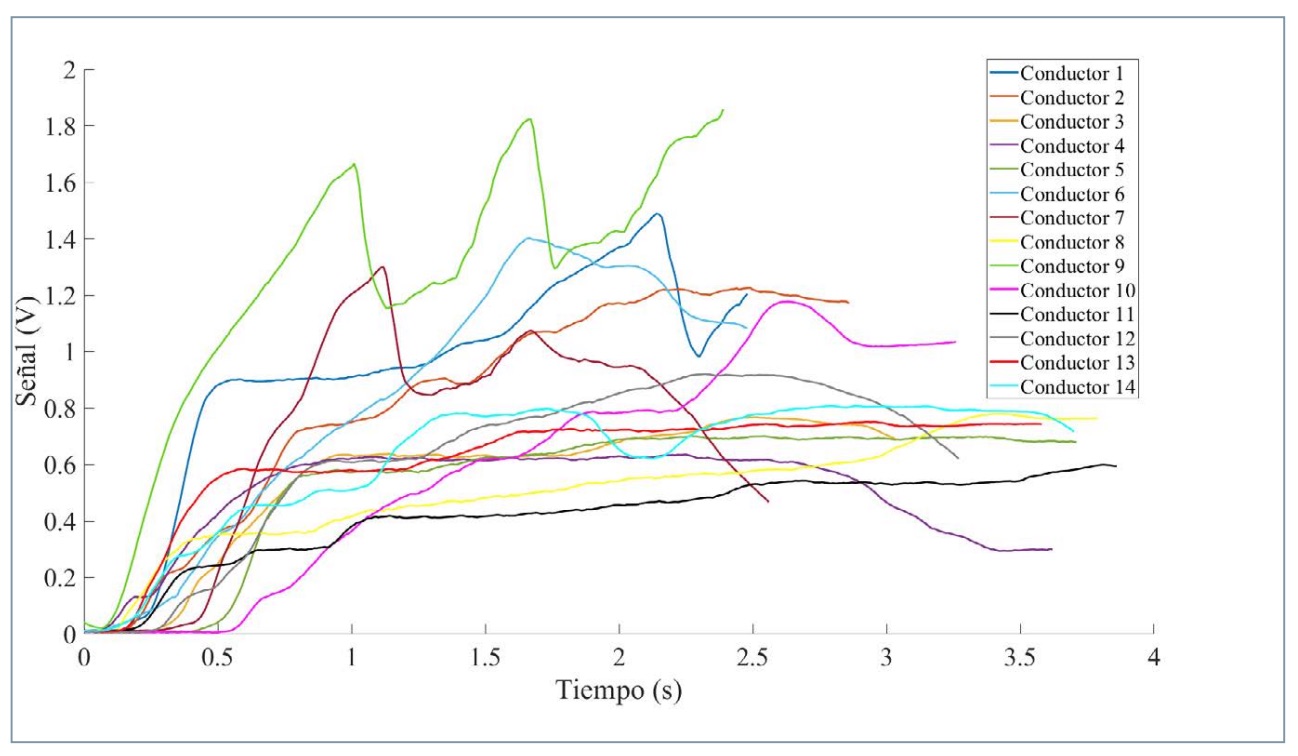
A continuación, se van a mostrar las curvas de las lecturas obtenidas directamente por cada uno de los sensores de presión para los 14 conductores. A modo de ejemplo, se muestran las curvas correspondientes a ensayos realizados partiendo de una velocidad de 60 km/h.

En la figura 7 se muestra una comparativa de las curvas correspondientes a los valores medidos mediante el sensor de presión derecha para los distintos conductores. El conductor 9 registra el valor máximo de 1,9 V y realiza la frenada más rápida (2,39 s).

En la figura 8 se muestra una comparativa de las curvas correspondientes a los valores obtenidos a través del sensor de presión izquierda para los distintos conductores. El conductor 9 registra el valor máximo de valor 1,86 V.

Metodología de análisis de los resultados
Para estudiar los 98 ensayos experimentales realizados para este trabajo y poder utilizar los datos registrados durante estos en los sistemas de RNA que se van a proponer en el siguiente punto, se han de definir nuevos conceptos, a modo de indicadores, que ayudarán a la caracterización de una frenada.

Lo primero que se hace es ajustar a un polinomio las curvas que representan la evolución temporal de las medidas reales obtenidas por los sensores de presión durante cada frenada.

Conocida la función de ajuste es posible calcular el área encerrada bajo la curva. Aquí aparece el indicador “qr” que se define como la integral de la función ajustada desde el inicio de la frenada hasta el final de esta. El indicador “qt ” proporciona información significativa en cuanto a la magnitud de la frenada, pero también resulta importante conocer cómo se distribuye temporalmente la frenada.

Por tanto, para conocer cómo se distribuye temporalmente la frenada se divide el tiempo total de la frenada en una cantidad fija de divisiones. Calculando el área bajo la curva de ajuste para cada división efectuada es posible tener una representación de la manera en la que se distribuye la medida total de magnitud medida. El vector que almacena esta información recibe el nombre de “qv ”.

Si se divide “qt ” entre el tiempo que tarda en ejecutarse la frenada, se obtiene el indicador denominado “vfillt ”.

Igual que antes, si “vfillt ” se integra por divisiones en función del tiempo, se obtiene la representación temporal de la evolución de la frenada. Este concepto se denomina “vfillv ”.

Arquitectura de los modelos de RNA diseñados
En este apartado se justifican las decisiones tomadas durante la implementación de los modelos de RNA que se presentan en este trabajo.

Se ha elegido la arquitectura de RNA Perceptrón Multicapa con entrenamiento mediante algoritmo backpropagation debido a su capacidad para interpretar e interpolar datos, crear relaciones entre parámetros de entrada y de salida y su facilidad de uso y versatilidad [7, 8].

Un aspecto fundamental en el diseño de la arquitectura de un Perceptrón Multicapa es decidir las capas en las que se disponen las neuronas. Las características de las capas de entrada y salida dependen del problema que se pretenda resolver, dado que la cantidad de neuronas necesarias en cada una de estas capas se determina atendiendo a la naturaleza de los patrones de entrada y de la salida que se pretende estimar. La capa oculta alberga las neuronas responsables de aproximar funciones no lineales, relacionando de esta manera las capas de entrada y salida. A la hora de elegir el número adecuado de capas y neuronas ocultas que conforman el sistema se tendrá en cuenta que, para el caso de Perceptrón Multicapa, basta con solo una capa oculta para aproximar con alto grado de eficacia cualquier función compleja [9, 10]. Por otro lado, el número de neuronas ocultas ha de ser el adecuado para lograr una correcta convergencia del modelo, por lo que es importante estudiar también la sensibilidad de este parámetro en lo que a resultados obtenidos se refiere.

En este estudio, la capa de entrada estará compuesta por dos neuronas que se corresponden con las variables de entrada del sistema diseñado: velocidad longitudinal y distancia de frenado. El motivo que justifica tal decisión está amparado en el equipamiento de los vehículos que se comercializan actualmente y que dan soporte a los sistemas de seguridad que incorporan los mismos, evitando de esta manera la instalación de nuevos sensores. La velocidad es un dato fácil de conocer en todo momento para cualquier vehículo; del mismo modo, y gracias a los sistemas de detección que montan los automóviles actuales, es posible obtener información de la distancia frontal del mismo hasta un punto (objeto en la calzada, otro vehículo, etc.). Este segundo valor sería el espacio del que dispone el vehículo para detenerse.

El objetivo de la RNA planteada es obtener el valor de la presión en el circuito de frenos; esta será la variable de salida del sistema.

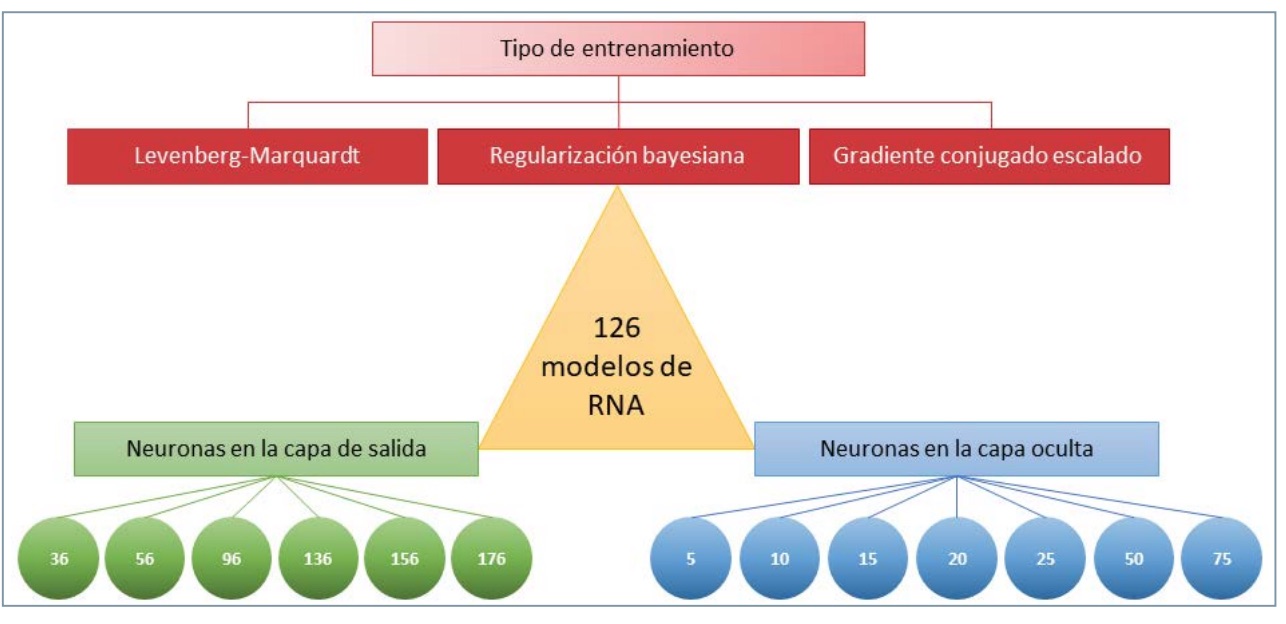
Dentro del modelo de RNA utilizado se plantean distintas variaciones a fin de optimizar el rendimiento de la misma. De este modo, se prueban capas de salida con diferente número de neuronas. Los casos planteados recogen 36, 56, 96, 136, 156 y 176 neuronas. A cada una de estas neuronas se le asigna, de manera individual, un determinado valor numérico.

Los datos con los que se trabaja en la RNA han sido redefinidos de cara a poder operar con ellos de forma homogénea a partir de la lectura de los sensores embarcados en el vehículo. De este modo, se relaciona la lectura de cada uno de los sensores utilizados con el tiempo que ha tardado en producirse la frenada para, así, discretizar dicha lectura y hacerla extrapolable a cualquier caso estudiado. Se ha analizado la influencia del número de divisiones en las que se discretizan estos valores y la regresión ofrecida por la RNA. Se plantean sistemas de 5, 10, 20, 30, 35 y 40 divisiones que coinciden con 36, 56, 96, 136, 156 y 176 neuronas en la capa de salida, respectivamente.

Las neuronas de la capa de salida se corresponden con la capacidad de frenada (qt ) y la intensidad puesta en juego para desarrollar la capacidad de frenada (vfillt ), valores estadísticos que permiten caracterizar la frenada de un vehículo automóvil, qt , vfillt , qv y vfillv , todo esto para los dos sensores de presión (derecha e izquierda). Además, se trabaja con las medias y desviaciones estándar de los datos leídos a fin de respaldar el entrenamiento de la RNA. El valor de qt se discretiza para las configuraciones planteadas de 5, 10, 20, 30, 35 y 40 divisiones y los valores discretizados se agrupan en el vector qv . De la misma forma, se discretiza vfillt para 5, 10, 20, 30, 35 y 40 divisiones y los valores discretizados se acumulan en el vector denominado vfillv .

De igual manera, se plantean sistemas cuyo elemento diferenciador es la cantidad de neuronas que alberga la capa oculta (5, 10, 15, 20, 25, 50 y 75).

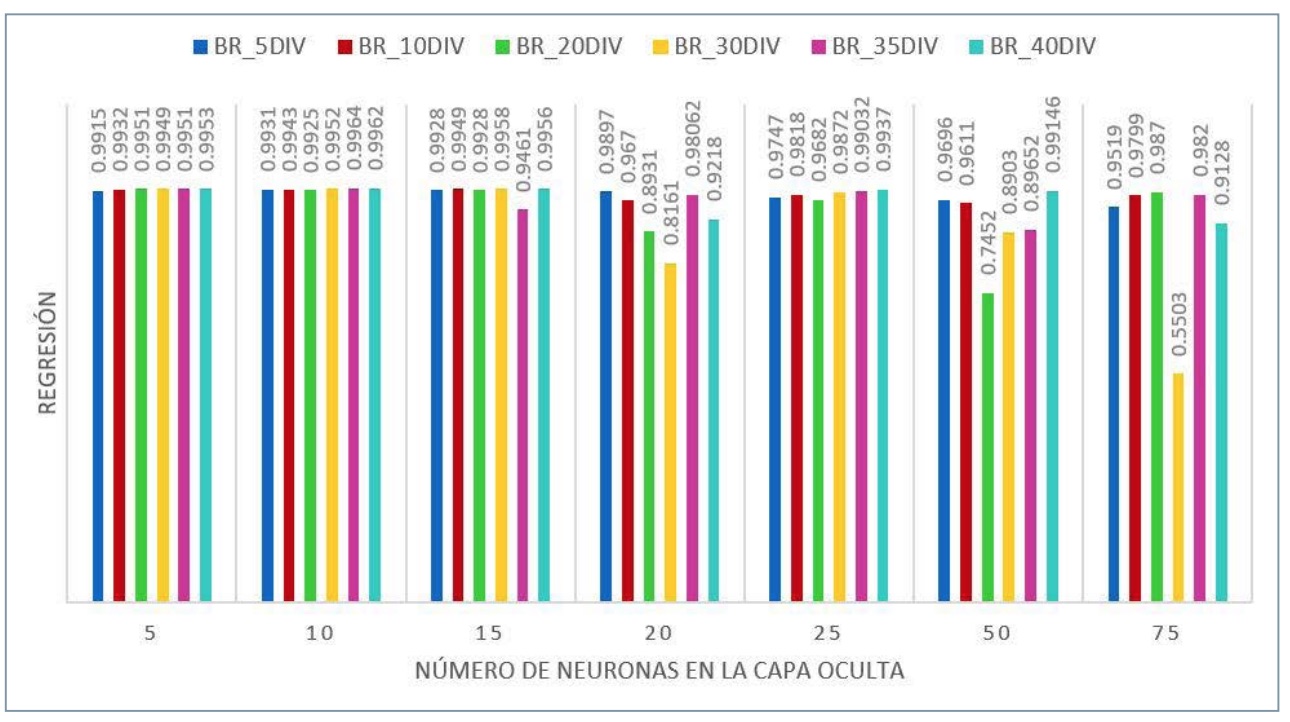
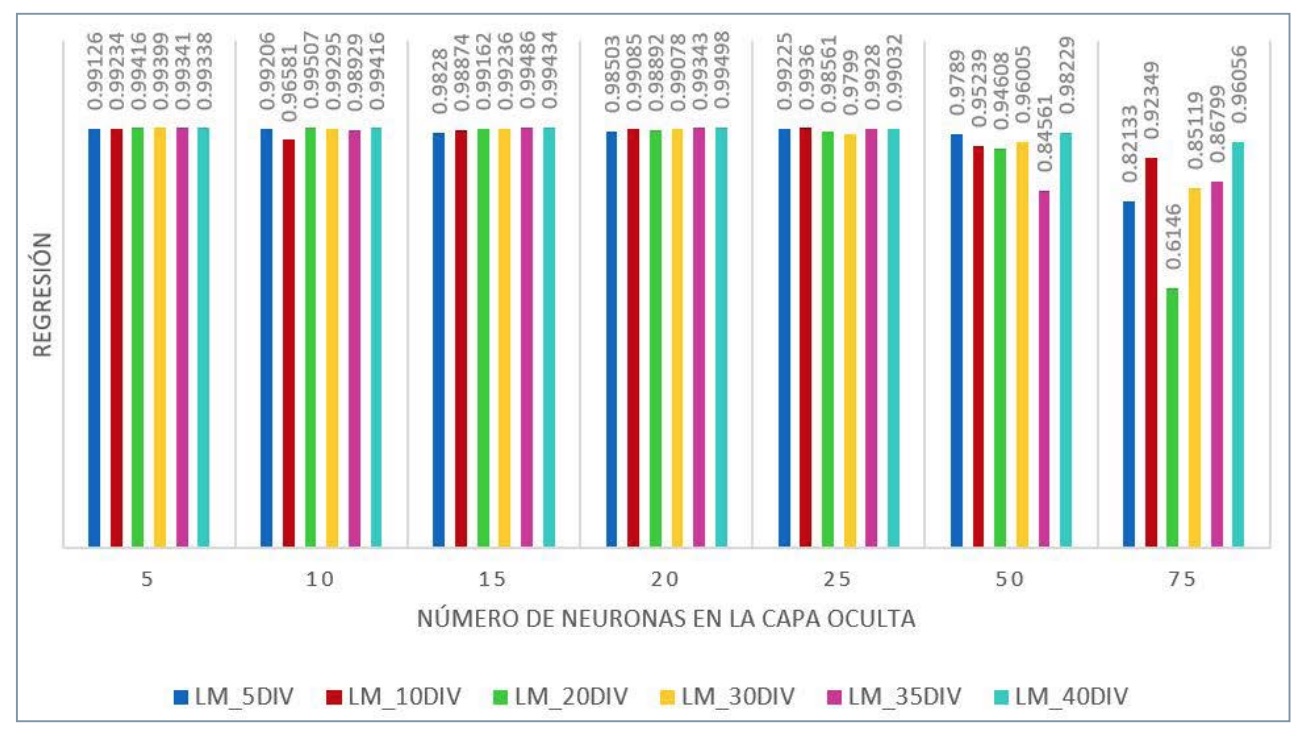
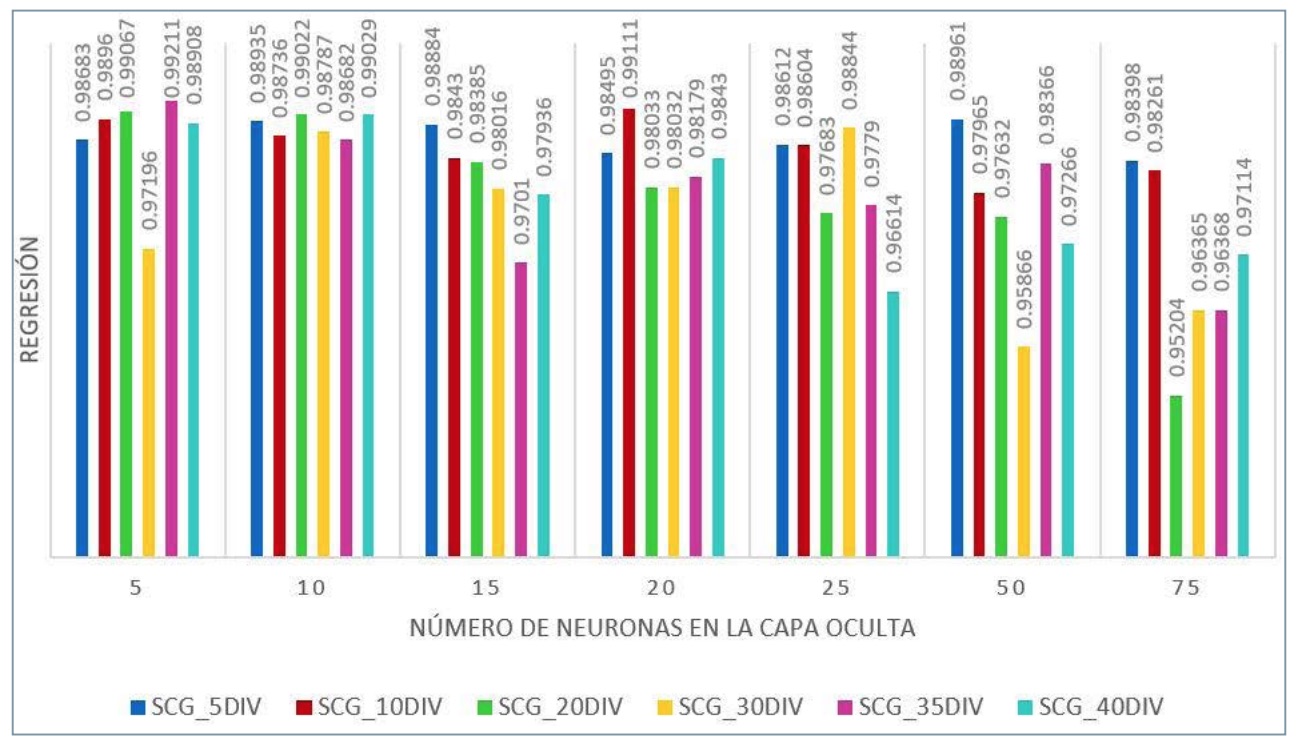
El tipo de entrenamiento al que se somete la RNA también es una importante elección. Se plantean, en combinación con el número de divisiones y la cantidad de neuronas que alberga la capa oculta, tres tipos distintos de entrenamiento: Levenberg-Marquardt (LM), regularización bayesiana (BR) y gradiente conjugado escalado (SCG) (Fig. 9).

La función de activación asociada a la capa oculta es de tipo sigmoidal, mientras que la capa de salida estará gobernada por funciones de tipo lineal. La capa de entrada es función directa a la capa oculta, por lo que se puede considerar que su función es escalón, proporcionando directamente los valores de entrada a la capa oculta.

La función de salida que se ha tomado para todas las neuronas es la identidad, de tal manera que la señal de salida de cada neurona coincide con su propio estado de activación.

El último paso será definir la interacción entre las neuronas que conforman la RNA. En este caso, y de manera extensiva para todas las capas y neuronas, se ha utilizado una conexión hacia delante (feedforward) en las relaciones entre las distintas neuronas del sistema.

Con el conjunto de variables comentadas, en combinación con el número de divisiones de los datos discretizados, el tipo de entrenamiento utilizado y el número de neuronas de la capa oculta del sistema, se ha procedido a simular un abanico de sistemas distintos con el fin de conocer cuál de ellos genera un mejor resultado. En las figuras 10, 11 y 12 se muestra la influencia de los distintos parámetros comentados en la sensibilidad de la RNA atendiendo al grado de regresión de los valores de entrada con los devueltos por el sistema en su proceso de prueba.

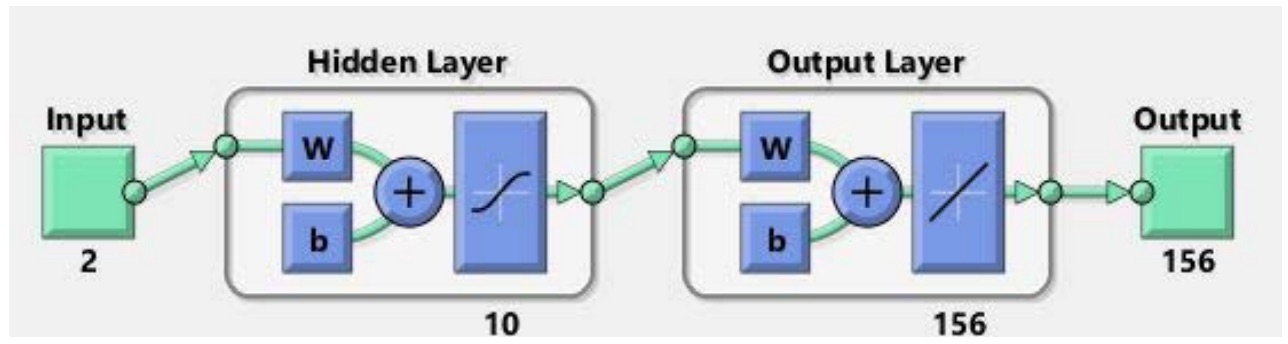
Todos los modelos tienen un elevado grado de regresión. No obstante, y dado que el coste computacional es despreciable (el entrenamiento de la red no se realiza en tiempo real, solo el proceso de simulación y estimación de parámetros se produce en tiempo real), se ha elegido una RNA con los siguientes parámetros (Fig. 13).

– Número de neuronas en la capa de entrada: 2.

– Número de neuronas en la capa oculta: 10.

– Número de neuronas en la capa de salida: 156.

– Tipo de entrenamiento: regularización bayesiana.

– Divisiones de los vectores de datos: 35.

Las 156 neuronas que componen la capa de salida se corresponden con:

– Posición 1: representa el valor de la capacidad de frenada medido por el sensor de presión derecha (qt ).

– Posición de 2 a 36: vector que divide en 35 el valor de la capacidad de frenada medido por el sensor de presión derecha atendiendo al tiempo que tarda el vehículo en detenerse (qv ).

– Posición 37: representa la manera en la que el sensor de presión derecha alcanza la capacidad de frenada total, proporcionando información de “cómo se produce la frenada en el tiempo” (vfillt ).

– Posición de 38 a 72: vector que divide en 35 el valor de vfillt relativo al sensor de presión derecha.

– Posición 73 a 78: valores estadísticos para la caracterización de la frenada en lo que se refiere al sensor de presión derecha.

– Posición 79: representa el valor de la capacidad de frenada medido por el sensor de presión izquierda (qt ).

– Posición de 80 a 114: vector que divide en 35 el valor de la capacidad de frenada medido por el sensor de presión izquierda atendiendo al tiempo que tarda el vehículo en detenerse (qv ).

– Posición 115: representa la manera en la que el sensor de presión izquierda alcanza la capacidad de frenada total, proporcionando información de “cómo se produce la frenada en el tiempo” (vfillt ).

– Posición de 116 a 150: vector que divide en 35 el valor de vfillt relativo al sensor de presión izquierda.

– Posición de 151 a 156: valores estadísticos para la caracterización de la frenada en lo que se refiere al sensor de presión izquierda.

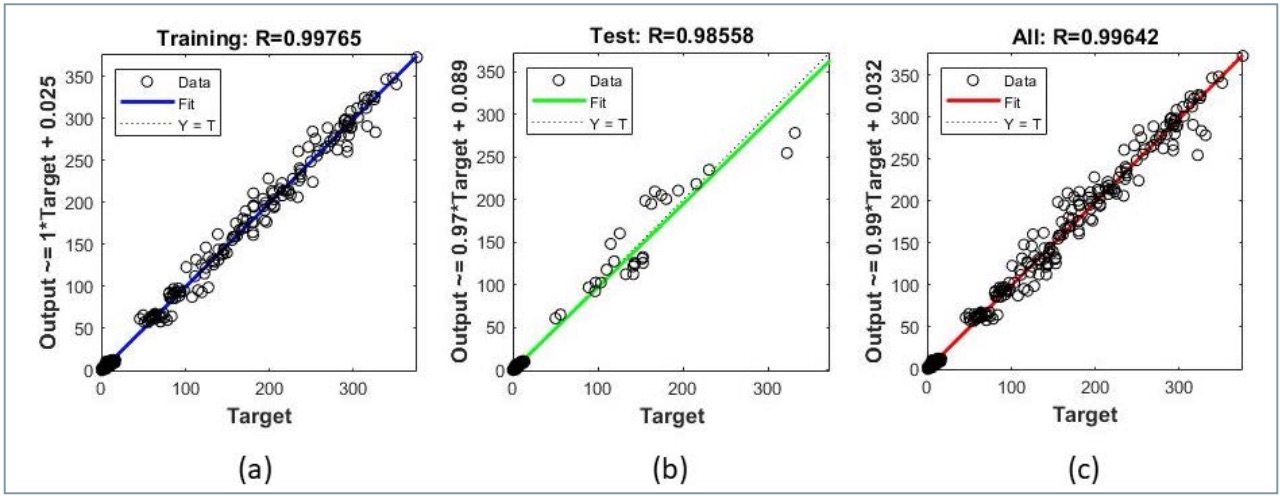
Los valores de regresión (R), parámetro que mide la correlación entre las salidas de la red y los datos objetivo, obtenidos para la fase de entrenamiento y de prueba, se muestran en la figura 14. Como combinación de estas fases se puede concretar el valor de regresión obtenido para el total del sistema de valor 0,99642.

Resultados de la estimación de parámetros de frenado
En este apartado se muestran los resultados obtenidos tras las distintas simulaciones de la RNA elegida. Estos valores son cotejados con los parámetros con los que se ha entrenado el sistema a fin de comprobar la correlación entre los valores objetivo y los valores simulados. Se han llevado a cabo simulaciones aleatorias cubriendo todo el rango de velocidades ensayadas.

Para una mejor comprensión de los resultados, se muestran a modo de ejemplo los relativos a una frenada realizada partiendo de una velocidad de 60 km/h.

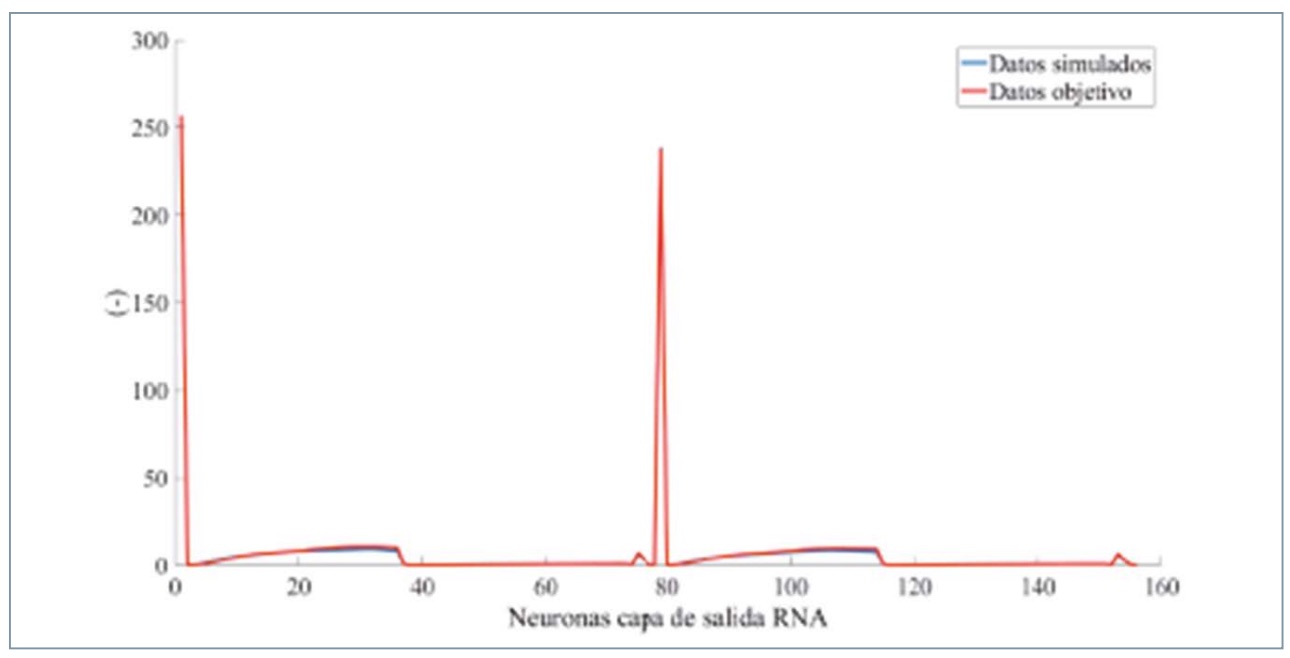
En la figura 15 se muestra la comparativa entre la simulación de los valores totales estimados por la RNA y la totalidad de los datos objetivo. Los valores totales coinciden con los parámetros, qt , vfillt , qv , vfillv y valores estadísticos de los dos sensores de presión.

Como se observa en la figura 15, las líneas que representan las simulaciones realizadas a partir de los valores estimados y los datos objetivo prácticamente se solapan, señal de una RNA con un alto grado de ajuste y convergencia. Es importante comentar que, por la naturaleza de los datos utilizados en el sistema, la capa de salida está formada por un vector de variables que toman distintos valores numéricos. Debido a esto, a la hora de tratar los resultados no se han tenido en cuenta las unidades de medida, y se ha dado importacia al valor numérico de los datos e interpretando cada uno por su posición.

Seguidamente, se divide la figura 15 para estudiar los resultados de cada parámetro de manera independiente. En la figura 16 se compara la simulación de los valores estimados por la RNA con los datos objetivo relativos a la capacidad de frenada (qt ) para los dos sensores de presión.

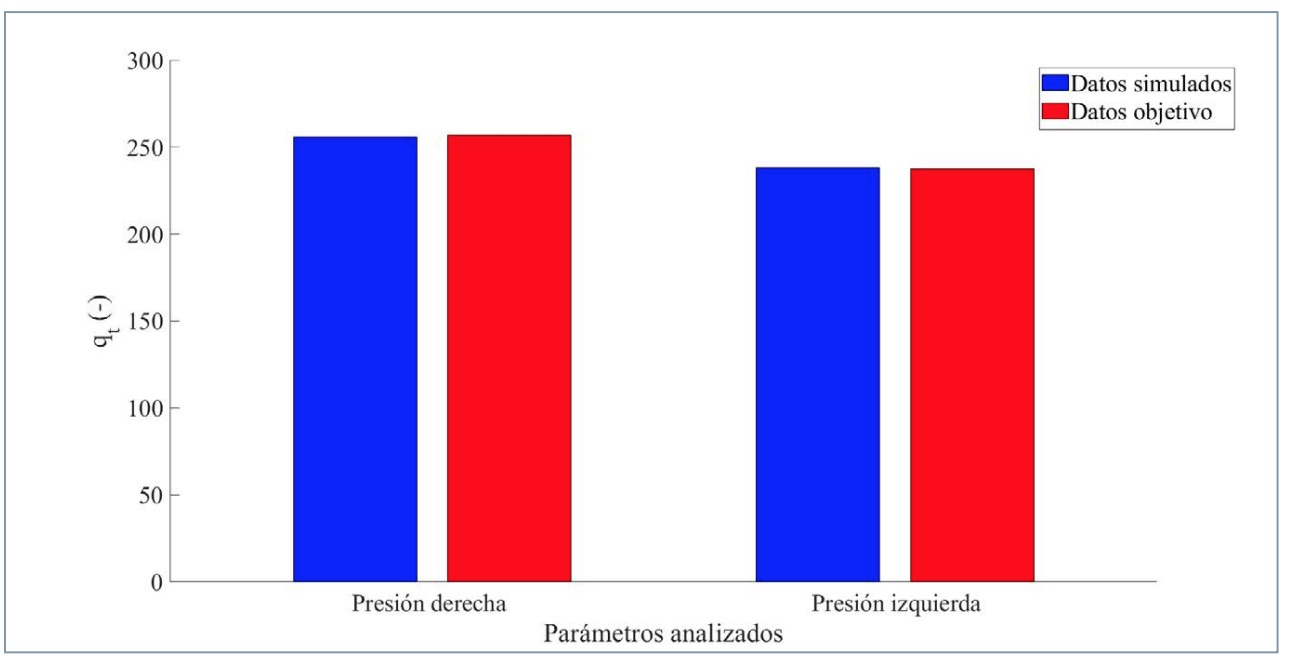
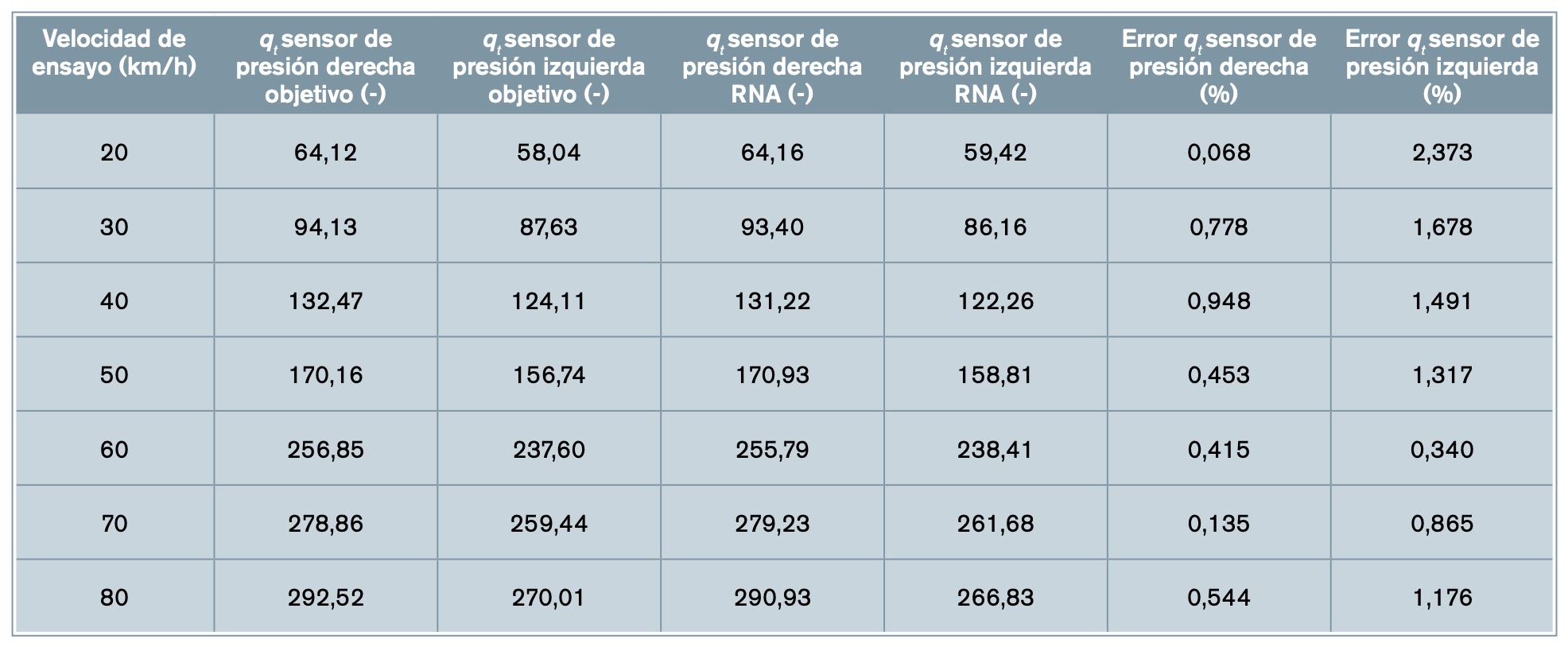
El valor del dato objetivo del parámetro qt relativo al sensor de presión del lado derecho es 256,85 y el valor estimado por la red 255,78. Por tanto, el error es del 0,41%. El valor del dato objetivo de qt para el sensor de presión del lado izquierdo es 237,60 y la red estima un valor de 238,41, por ende, el error es del 0,34%. Se constata que el porcentaje de error alcanzado para los dos casos es muy reducido con una media del 0,38%.

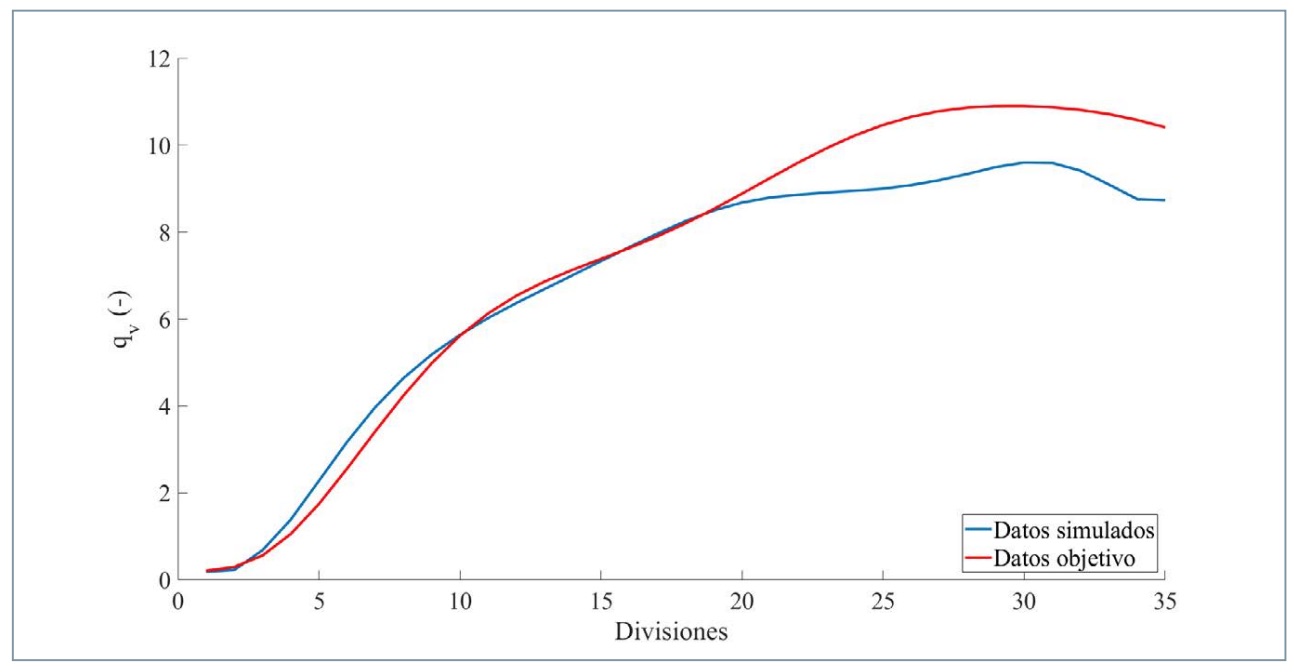
En la figura 17 se presenta la comparativa entre los datos simulados y los datos objetivo relativos a cómo evoluciona, en las 35 divisiones efectuadas, la capacidad de frenada en función del tiempo que tarda el vehículo en detenerse (qv ), para el sensor de presión derecha.

El error medio que se obtiene en las 35 divisiones es del 10,79%. Los errores máximos se dan en la división 4 y 5 del 31,38% y del 30,5%, respectivamente, y el mínimo es del 0,34% en la división 10.

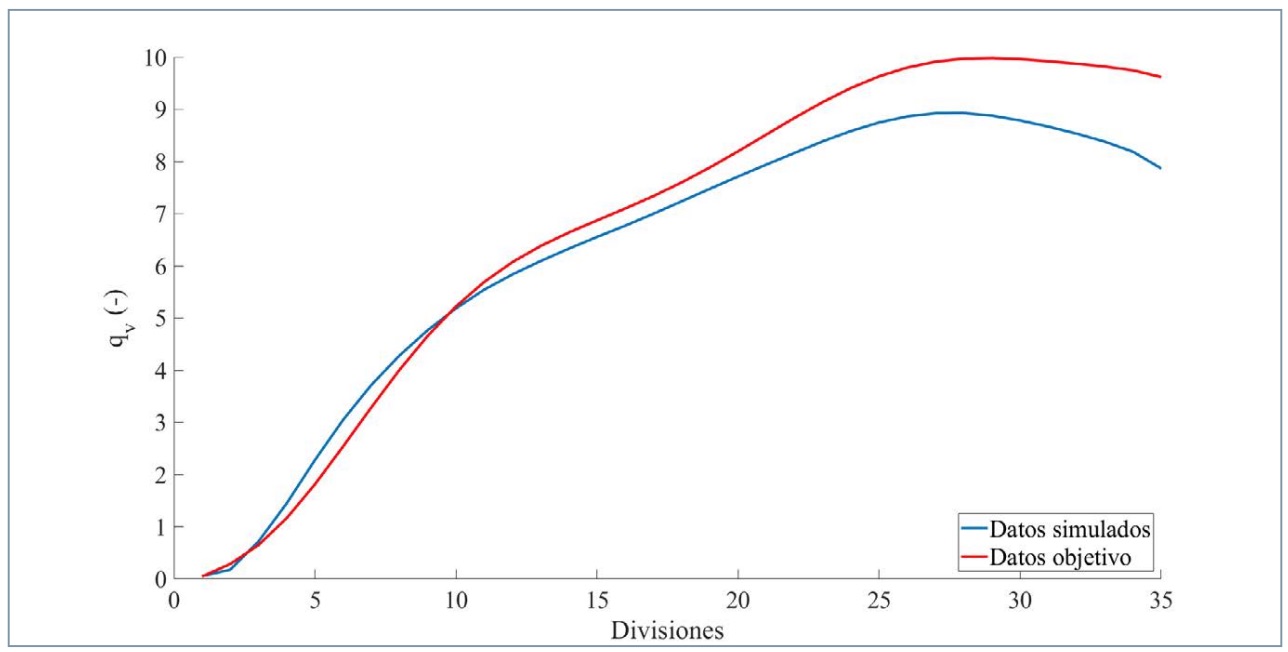
En la figura 18 se presenta la comparativa entre los datos simulados y los datos objetivo referentes a la evolución de qt , en las 35 divisiones efectuadas, para el sensor de presión izquierda.

El error medio que se obtiene en las 35 divisiones es del 10,62%. Los errores máximos se vuelven a registrar en la división 4 y 5 del 24,31% y del 25,69%, respectivamente, y el mínimo es del 0,72% en la división 10.

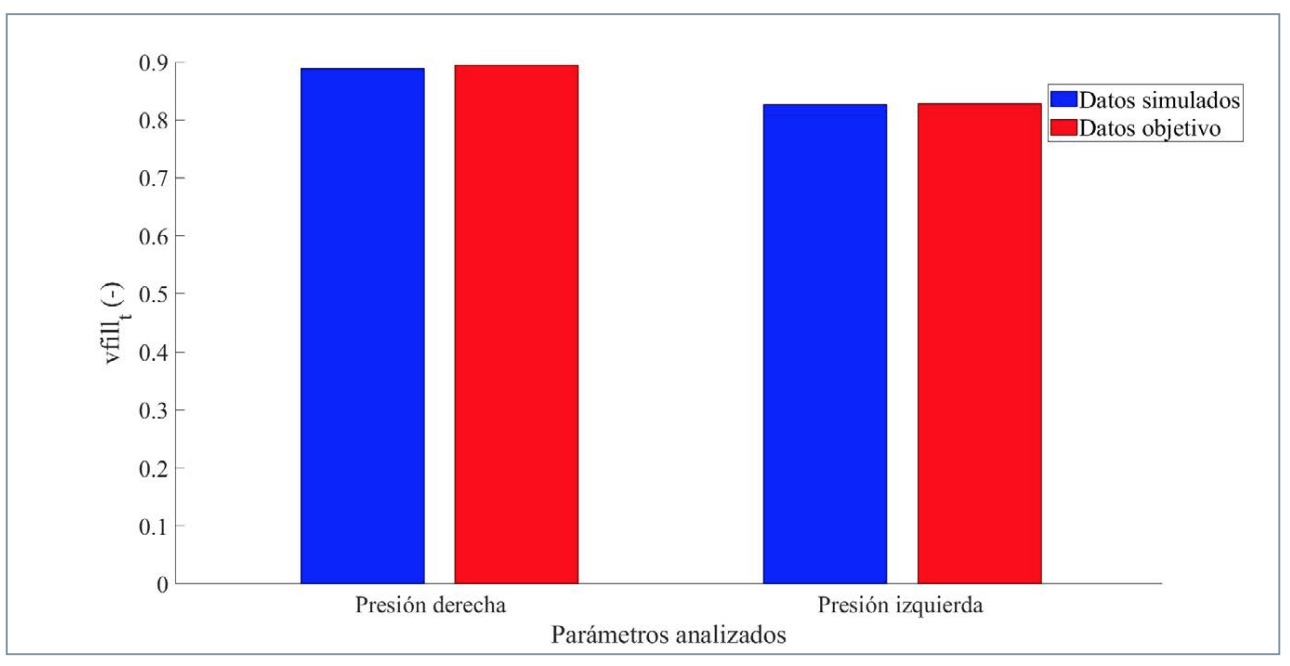
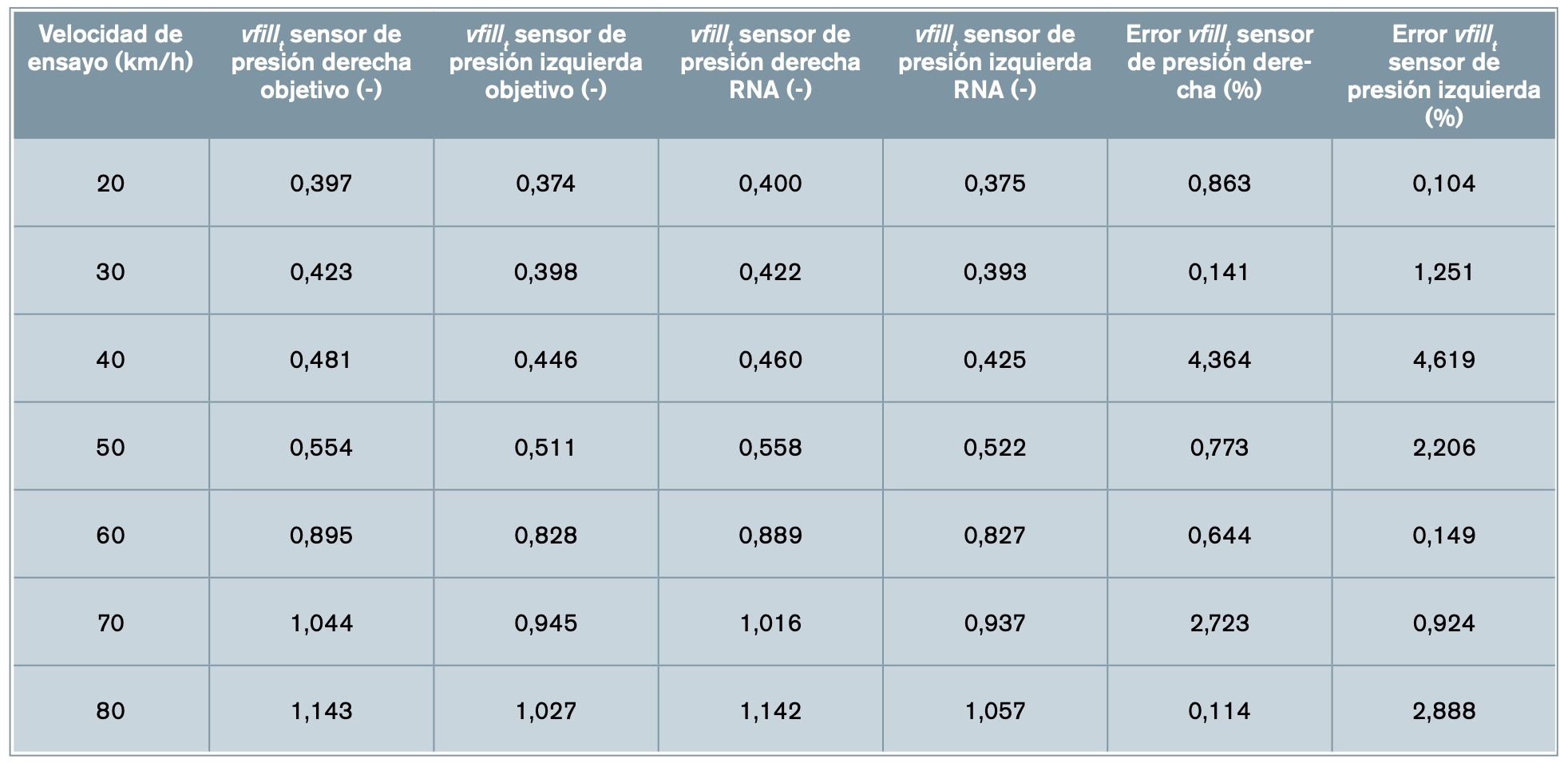
En la figura 19 se muestra la comparativa entre los valores estimados por la RNA y los datos objetivo para vfillt . La diferencia menor se obtiene para el sensor de presión izquierda, siendo el valor del dato objetivo de 0,828 y el valor estimado por la red 0,826 y para el sensor de presión derecha el objetivo es 0,895 y el valor estimado por la red 0,889. Esto se traduce en unos errores propiciados por el sistema de 0,15% y 0,64%, respectivamente.

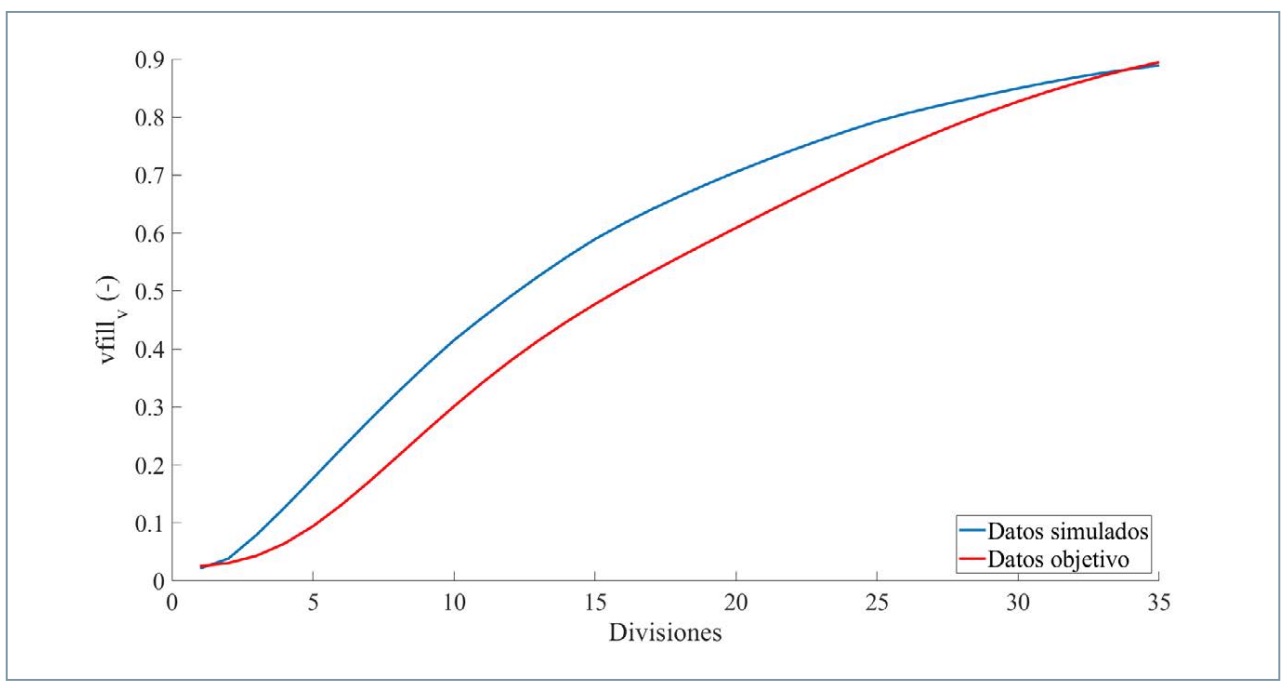
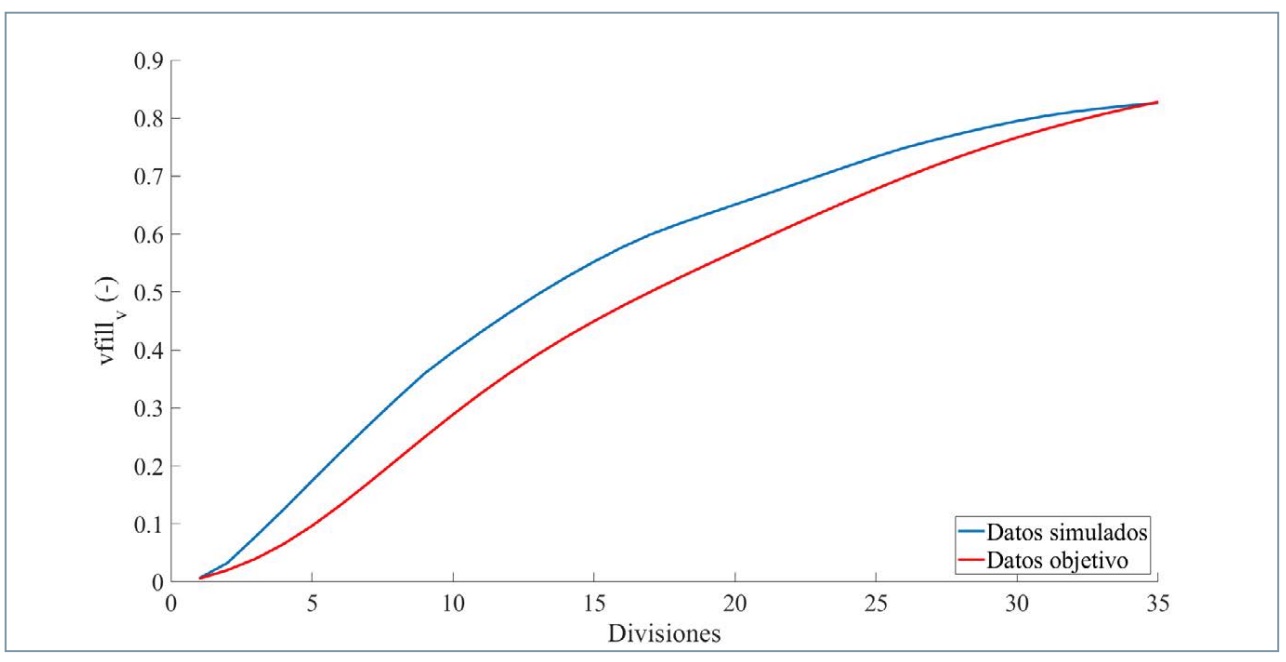
En la figura 20 se presenta la comparativa entre los datos simulados y los datos objetivo relativos a la manera en que el sensor de presión derecha alcanza la capacidad de frenada en función del tiempo que tarda el vehículo en detenerse (vfillv ).

En la figura 21 se presenta la comparativa entre los datos simulados y los datos objetivo relativos al parámetro vfillv para el sensor de presión izquierda.

Para el parámetro vfillv el error medio que se obtiene en las 35 divisiones es del 25,53% para el sensor de presión derecha y del 25,96% para el sensor de presión izquierda.

Como se ha comentado anteriormente, se han realizado simulaciones de forma aleatoria para todo el rango de velocidades de ensayo. A continuación, se muestran los errores derivados de los parámetros qt y vfillt en comparación con los datos empíricos.

En la tabla 1 se muestran los valores objetivo y simulados de qt de los sensores de presión y su error.

El error medio de la capacidad de frenada de todas las simulaciones es del 0,48% y del 1,32% para el sensor de presión derecha y el sensor de presión izquierda, respectivamente. La desviación estándar de la capacidad de frenada de todas las simulaciones es del 0,32% para el sensor de presión derecha y del 0,64% para el sensor de presión izquierda. En la tabla 2 se muestran los valores objetivo y simulados de vfillt y su error.

El error medio de vfillt de todas las simulaciones es del 1,37% para el sensor de presión derecha y del 1,73% para el sensor de presión izquierda. La desviación estándar de todas las simulaciones es del 1,58% y del 1,63% para el sensor de presión derecha e izquierda, respectivamente.

Validación de los resultados frente a la lectura directa de los sensores
En este punto se va a mostrar la comparativa entre los valores de las simulaciones realizadas por la RNA y los valores empíricos recogidos por los sensores durante los ensayos experimentales.

Los valores estimados por la RNA están representados en el tiempo en el cual el sistema estima que se producirá la frenada.

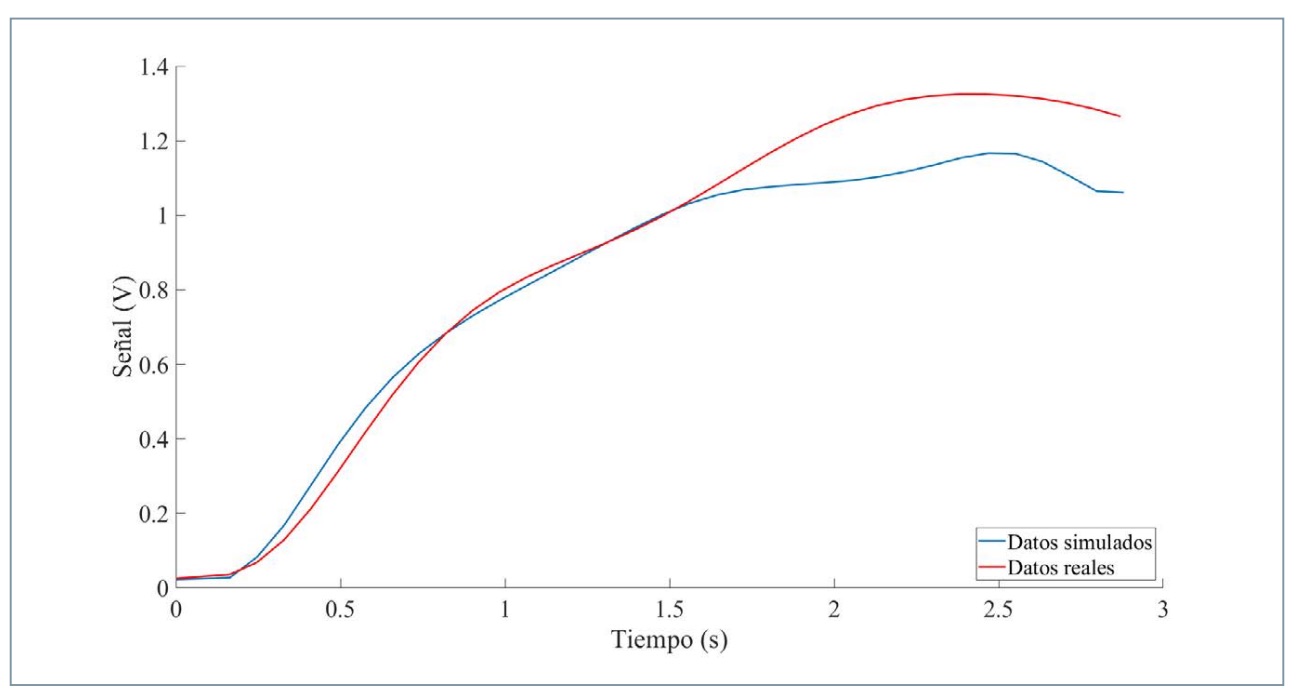
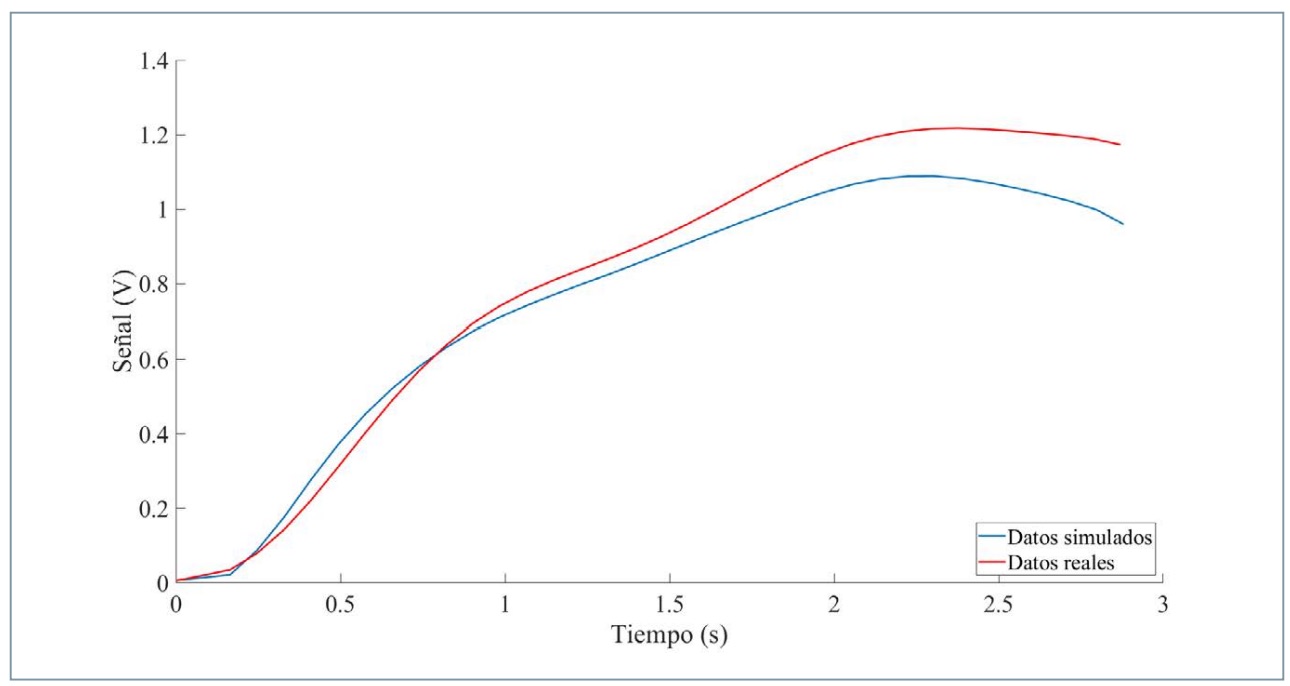
En la figura 22 se observa la comparativa entre los datos ofrecidos por la RNA al simular una frenada a una velocidad de 60 km/h y los datos recogidos por el sensor de presión derecha durante la realización de este ensayo.

En la figura 23 se muestran las diferencias relativas al sensor de presión izquierda y la estimación de su comportamiento para el mismo ensayo.

Conclusiones
Las contribuciones del trabajo que se ha realizado, las conclusiones y las líneas futuras de investigación del mismo se resumen a continuación.

Se ha instrumentado un vehículo automóvil mediante el empleo de sensores de presión incorporados en los circuitos hidráulicos independientes de las ruedas delanteras y una célula de carga instalada sobre el pedal de freno. Se ha demostrado que los sensores de presión son adecuados para medir con precisión bajo condiciones dinámicas y han proporcionado información relevante para poder caracterizar una frenada. Igualmente, se ha embarcado un receptor GPS en el vehículo.

Se han realizado ensayos experimentales en condiciones controladas tanto para la pista como para el vehículo. El conductor realiza, siguiendo una trayectoria rectilínea, una serie de frenadas con el vehículo hasta detenerlo. Las frenadas se realizan partiendo de velocidades de 20, 30, 40, 50, 60, 70 y 80 km/h.

Para el análisis de los datos, se han definido los parámetros qt , vfillt , qv , y vfillv con objeto de operar con los datos recogidos por los sensores de forma homogénea en el diseño del estimador.

Se ha diseñado un sistema capaz de caracterizar la frenada de un vehículo automóvil. En todos los casos, las curvas comparativas entre los datos obtenidos de las simulaciones y los datos objetivo de los sensores de presión derecha e izquierda prácticamente se solapan y muestran que ambas siguen iguales patrones de comportamiento. Las simulaciones de vfillv son las que presentan mayores diferencias al compararlas con los datos objetivo. No obstante, las tendencias son similares.

A la vista de los resultados obtenidos se puede garantizar que la técnica propuesta basada en redes neuronales artificiales permite estimar la capacidad de frenada con un mínimo grado de error. El sistema estima la capacidad de frenada con un error medio del 0,48% y del 1,32% para el sensor de presión derecha y el sensor de presión izquierda, respectivamente.

Para trabajos futuros se pueden diseñar nuevos ensayos en los que se propongan sensores distintos y con diferentes maniobras que simulen la conducción real, distintas superficies de rodadura, condiciones meteorológicas determinantes, múltiples trayectorias, etc. Se pueden emplear otros métodos de estimación como pueden ser Fuzzy Logic, filtro de Kalman o filtro H-Infinity. Con una gran batería de datos es posible realizar mayor cantidad de parametrizaciones a la hora de diseñar la RNA que gobierne el sistema sobre el que se está trabajando. Es interesante optimizar el método propuesto de estimación orientado al trabajo para el cual es requerido, analizando la sensibilidad a las ponderaciones de datos.

---

Referencias

[1] Park E. J., Stoikov D. “A performance evaluation of an automotive magnetorheological brake design with a sliding mode controller”, Mechatronics 16, 405-416 (2006).

[2] D’alfio N., Morgando A., Sorniotti A. “Electrohydraulic brake systems: design and test through hardware-in-the-loop simulation”, Veh. Syst. Dyn. 44, 378-392 (2006).

[3] Castillo J. J., Cabrera J. A., Carabias E., Simón A. “Estimación de parámetros en sistema de frenado”, Actas del XIX Congreso Nacional de Ingeniería Mecánica, Castellón (2012).

[4] Doumiati M., Victorino A., Charara A., Lechner D. “Estimation of vehicle lateral tire-road forces: a comparison between extended and unscented Kalman filtering”, en Proceedings of the European Control Conference, Budapest, 2009.

[5] Doumiati M., Victorino A., Lechner D., Baffet G., Charara A. “Observers for vehicle tyre/road forces estimation: experimental validation”, Veh. Syst. Dyn. 48, 1345-1378 (2010).

[6] Shraim H., Ouladsine M., Fridman L., Romero M. “Vehicle parameter estimation and stability enhancement using sliding modes techniques”, Int. J. Veh. Des. 48, 230-254 (2008).

[7] Zhang L., Subbarayan G. “An evaluation of backpropagation neural networks for the optimal design of structural systems: Part I. Training procedures”, Computer Methods in Applied Mechanics and Engineering 191, 2873-2886 (2002).

[8] Ince R. “Prediction of fracture parameters of concrete by Artificial Neural Networks”, Eng. Fract. Mech. 71, 2143-2159 (2004).

[9] Hornik K., Stinchcombe M., White H. “Multilayer feedfoward networks are universal approximators”, Neural Networks 2, 359-366 (1989).

[10] Cybenko G. “Approximation by superpositions of a sigmoidal function”, Mathematics of Control, Signals, and Systems 2, 303-314 (1989).