Aplicación de los métodos de ayuda a la toma de decisión para el análisis temporal de la contaminación ambiental en una ciudad
Application of decision-making methods for the temporary analysis of environmental pollution in a city
Emilio José García Vílchez (1)
Resumen
Cualquier emisión industrial, de tráfico o incluso doméstica, lleva aparejado un cierto nivel de riesgo para la salud de las personas. Por ello, es responsabilidad de las autoridades la intervención y la investigación de dichas emisiones para lograr que la calidad del aire que respiramos todos los ciudadanos se mantenga siembre en el nivel óptimo posible. Debido a la normativa ambiental europea, traspuesta en España en el RD 102/2011 del 18 de enero, se exige que debe haber, al menos, un punto de medición de la contaminación por cada 50.000 km2 o dos millones de habitantes. Para este fin, los Estados miembros deben de disponer de una red para el control de la contaminación atmosférica (RCCA) con el objetivo de monitorizar la contaminación ambiental y poder actuar en consecuencia en función de los resultados obtenidos. Este seguimiento debe realizarse los 365 días del año realizando mediciones de los parámetros exigidos en dicho RD en diferentes puntos durante las 24 horas, para así tener un conocimiento de lo que está sucediendo y poder tomar acciones en consecuencia en función de los valores de cada contaminante. Este artículo hace referencia a los datos recogidos por una RCCA de una ciudad de España formada por siete estaciones meteorológicas que han medido 12 parámetros ambientales durante el mismo periodo de tiempo y durante ocho años en total. Este periodo se ha seleccionado debido a que el año 2020 coincide con el estado alarma debido a la covid-19, por lo que la actividad tanto de vehículos como de industrias fue menor. En consecuencia, se dispone de un periodo de referencia para poder comparar la evolución de los contaminantes ambientales durante diferentes periodos de una manera agregada mediante el uso de métodos matemáticos para la ayuda de toma de decisión. Para ello, es necesario tratar los datos, ponderar y normalizar el conjunto de datos de cada periodo de cada año para, posteriormente, poder compararlos de manera objetiva mediante diferentes métodos matemáticos y poder extraer conclusiones de manera global en una clasificación de índices agregados anuales.
Palabras clave: Medición de la contaminación, análisis de contaminantes, métodos de ayuda a la toma de decisión, estaciones de medida de contaminantes.
Abstract
Any industrial, traffic or even domestic emission carries a certain level of risk to people’s health. For this reason, it is the responsibility of the authorities to intervene and investigate these emissions to ensure that the quality of the air that all citizens breathe is always maintained at the optimum possible level. Due to the European environmental regulations, transposed in Spain in RD 102/2011 of January 18th, it is required that there must be at least one pollution measurement point for every 50,000 km2 or two million inhabitants. To this end, the member States of European Union must have a Network for the Control of Air Pollution (NCAP) with the aim of monitoring environmental pollution and being able to act accordingly based on the results obtained. This monitoring must be carried out 365 days a year, making measurements of the parameters required in said the RD 102/2011 at different points during 24 hours in order to have an understanding of what is happening and to be able to take actions accordingly based on the values of each pollutant. This article refers to the data collected by a NCAP from a city in Spain made up of seven meteorological stations that have measured 12 environmental parameters during the same period of time and for a total of eight years. This period has been selected for this analysis because the year 2020 coincides with the Spanish state of alarm due to covid-19, so the activity of both vehicles and industries was lower. Therefore, there is a reference period to be able to compare the evolution of environmental contaminants during different periods in an aggregate manner using mathematical methods to aid decision-making. For this, it is necessary to treat, weight and normalize the data set for each period of each year to later be able to compare them objectively through different mathematical methods and thus to be able to draw conclusions globally in a ranking of annual aggregate index.
Keywords: Pollution measurement, pollutant analysis, decision support methods, pollutant measurement stations.
Recibido/received: 17/08/2023
Aceptado/accepted: 20/02/2024
1 Ingeniero técnico industrial en Química, ingeniero en Organización Industrial y doctor en Ingeniería de Procesos y Sistemas por la Universidad de Valladolid. Posgraduado en Logística e Ingeniería de la Calidad. Máster en Prevención de Riesgos Laborales. Más de 20 años de experiencia en la gestión de equipos en organizaciones nacionales e internacionales.
Autor para correspondencia: Emilio José García Vílchez, emigarvil@gmail.com
CÓDIGO UNESCO: 1209.03 Análisis de datos.
1. Fundamento teórico
Objetivos
Con este artículo se pretenden abordar los siguientes objetivos:
• Extraer los datos ambientales de la RCCA desde sus Bases de Datos Web para el periodo concreto establecido (del 15 de marzo al 21 de junio para los años 2016 al 2023) eliminando los datos anómalos.
• Normalizar, ponderar, agregar y analizar los datos descargados de la RCCA en diferentes periodos utilizando para ello los métodos de ayuda a la toma de decisión.
• Realizar una comparación objetiva de los datos para establecer una clasificación y conocer, por tanto, qué año es el que presenta un índice agregado ambiental mayor con un impacto ambiental menor para los ciudadanos.
• Extraer conclusiones sobre los resultados obtenidos.
Red de Control de la Contaminación Ambiental (RCCA) de estudio
La RCCA de estudio, de la que se han extraído los datos, consta de siete estaciones de medida localizadas en diferentes puntos de una ciudad de 198 km2 y con 300.000 habitantes. Está acreditada por la norma ISO 17025:2017, por lo que se garantiza la calidad de las mediciones realizadas.
Los instrumentos de medida localizados en todas las estaciones son totalmente automáticos y realizan la medida de forma continuada en el tiempo. Todos los instrumentos se encuentran unidos a un sistema de adquisición de datos (SAD) que, de forma instantánea, captura la información del instrumento cada 15 minutos y la incorpora secuencialmente a su propia base de datos para llegar a un centro de proceso de datos (CPD).
La comunicación entre las estaciones y el CPD se verifica a través de una red propietaria de fibra óptica que garantiza la máxima disponibilidad de datos e inmunidad frente a posibles ataques externos, un conocimiento en tiempo real de la evolución de un episodio y una inmunidad a fallos muy superior a la dependencia de una red pública de telecomunicaciones; también un coste de operación casi nulo comparado con otras opciones comerciales dedicadas punto a punto.
Cada instrumento de medida de la contaminación de los instalados en las estaciones verifica el análisis de la muestra de aire ambiente siguiendo una técnica oficial establecida por las diferentes normas reguladoras.
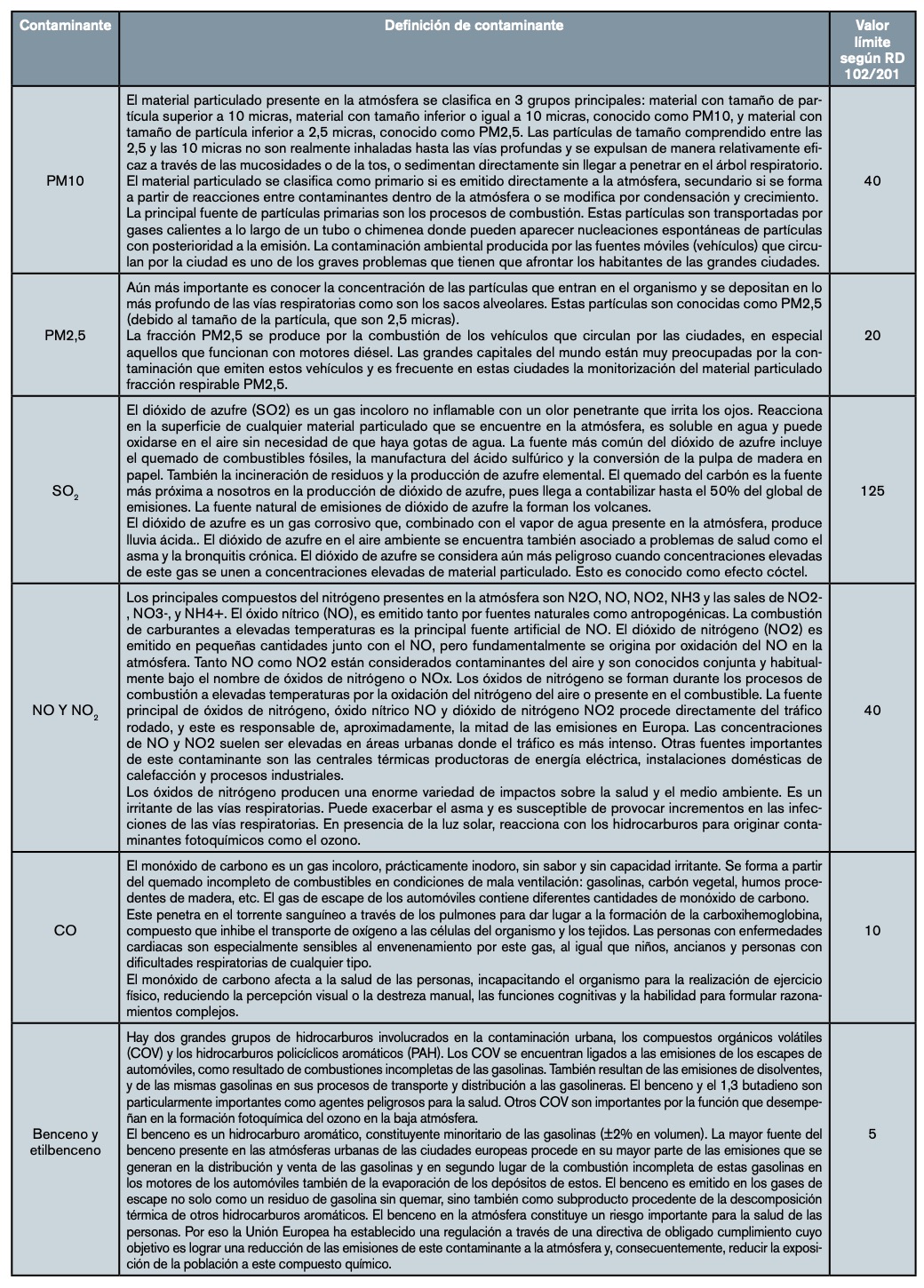
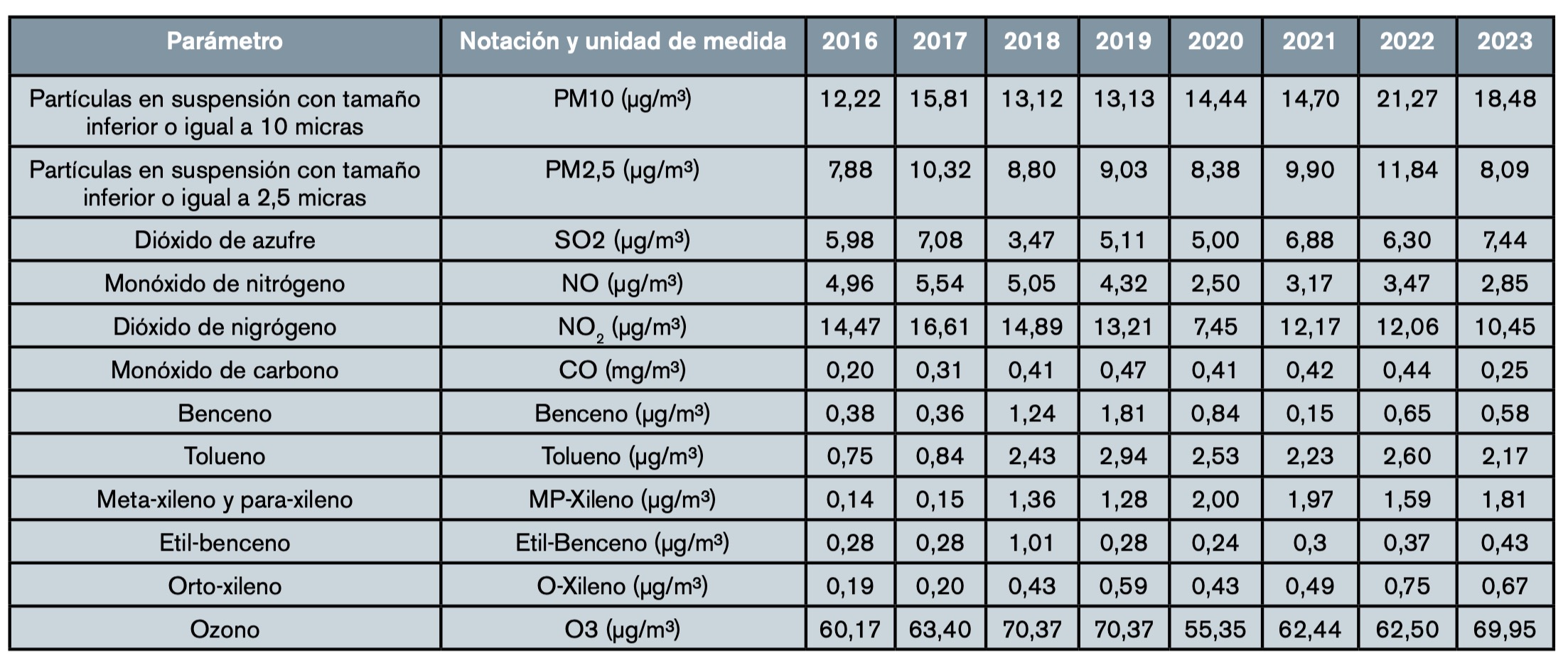
Los contaminantes medidos por la RCCA en sus diferentes estaciones de medida, así como sus valores límite diarios máximos según el RD 102/2011 del 18 de enero, son los establecidos de en la tabla 1.

Métodos de ayuda a la toma de decisión
A continuación, se presenta el soporte matemático que va a servir de ayuda en la normalización, ponderación, agregación y análisis de la serie temporal de datos para cada periodo para poder establecer una clasificación de ordenación de índices anuales.
La toma de decisiones puede considerarse una formalización del sentido común para aquellos problemas demasiado complejos en que este no puede ser utilizado de modo informal (Keeney, 1982).
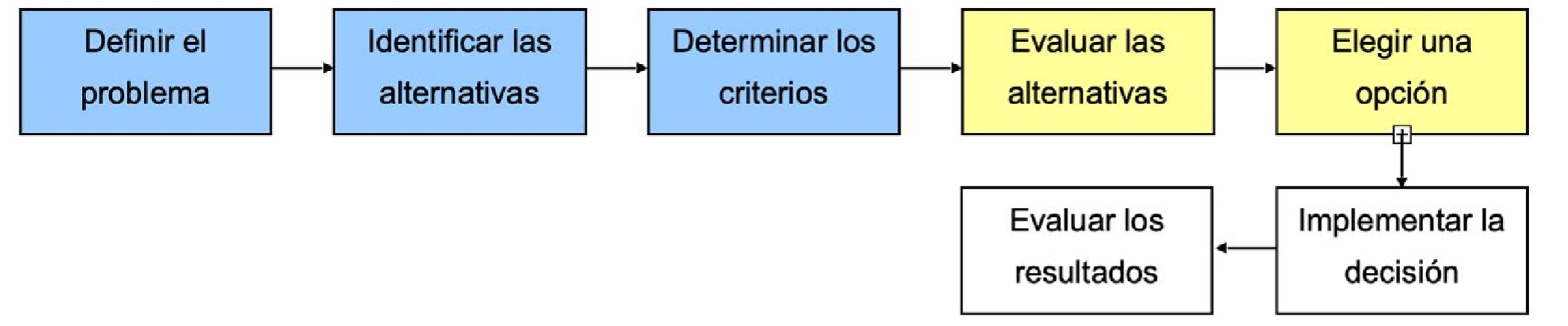
La toma de decisión se asocia a las primeras cinco etapas de un proceso de resolución de problemas (fig. 1). Se inicia en la identificación y la definición del problema y concluye en la selección de la alternativa, que es en sí la toma de decisión.
Agentes y elementos presentes en una toma de decisión
Según Chiavenato (2007), es necesario contar con diferentes elementos para llevar a cabo la toma de decisión de forma acertada:
• Decisor o analista. Es el responsable de la recogida de la información, de la determinación de los criterios a utilizar, de la construcción de las alternativas y de la selección de una de ellas.
• Alternativas. Es una de las posibles soluciones que se le puede dar al problema. Por la generalidad, las alternativas son diferentes, excluyentes y exhaustivas.
• Atributos y criterios. Consisten en los diferentes ejes de evaluación que se consideran para la elección de una alternativa. En algunas ocasiones, para establecer diferentes planos de igualdad y poder hacer la decisión más fácil y objetiva, se otorgan unos pesos a cada atributo.
• Pesos. Valores que hacen que un criterio sea más o menos importante frente a otro. Los pesos pueden ser cardinales u ordinales. De entre los diferentes métodos de asignación de pesos destaca el de la asignación directa, que está formado por el método de la ordenación simple, el método de la tasación simple, el método de las comparaciones sucesivas y el método de los eigenpesos.
• Matriz de decisión. Es la matriz formada por los pesos y las alternativas, con todas las valoraciones dos a dos. En esta matriz pueden coexistir valores en muy distintos rangos y unidades, por lo que hay que normalizar los datos a través del uso de los métodos del porcentaje del máximo, porcentaje del rango, porcentaje del total o el vector unitario.
(Hwang y Yoon, 1981 y Chen y Hwang, 1992, en Venkata, 2007).

Tipologías
La elección de la mejor opción se presenta cuando una alternativa supera al resto en todos los criterios (solución ideal). Esto no es lo que sucede normalmente, por lo que no existe dicha solución óptima. Los distintos problemas de decisión, tras diversas investigaciones, se agrupan en dos grandes categorías (White, 1990):
a. Toma de decisiones multiatributo
Está asociada con problemas en los que el número de alternativas está predeterminado, y el decisor tan solo debe seleccionar, clasificar u ordenar las diferentes alternativas. Dentro de esta categoría se encuentra los métodos con solución a priori y los métodos interactivos.
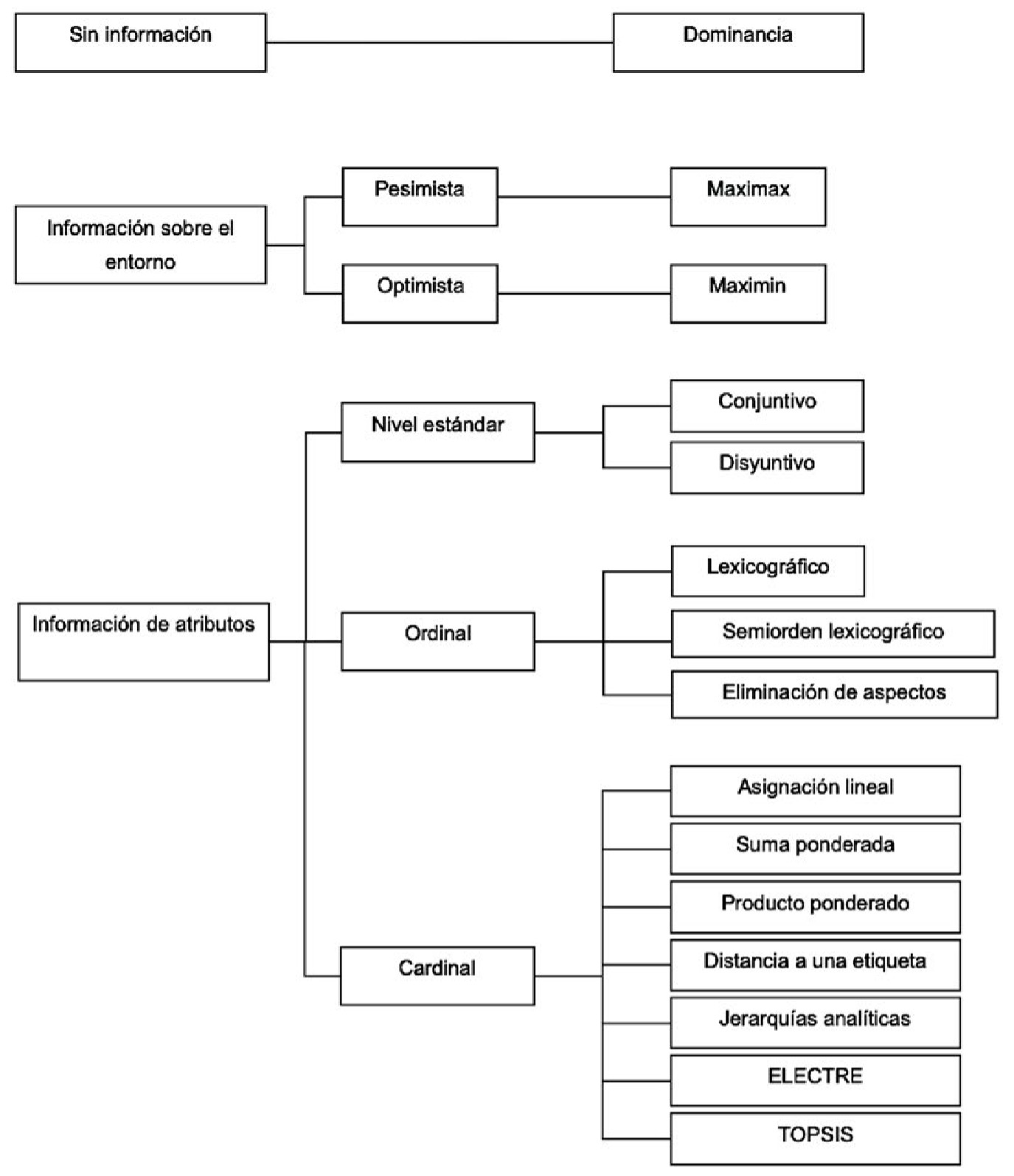
Los métodos más utilizados son los de solución a priori, en los que la información es obtenida, a priori, a partir de los datos suministrados por los decisores. La clasificación de estos métodos (fig. 2) se realiza según la información que tiene disponible el decisor, ya sea ordinal, cardinal (numérica) o estandarizada (Venkata, 2007).
b. Toma de decisiones multiobjetivo
En este caso está asociada con problemas en los que dichas alternativas no están determinadas a priori, y el propósito del decisor es obtener o diseñar la mejor alternativa con los recursos limitados de que dispone (como pueden ser el tiempo y el coste). Además de estas dos categorías principales, hay otros métodos denominados interactivos los cuales son progresivos. Se caracterizan por que el decisor se desplaza de una solución a la siguiente de forma interactiva, según la información facilitada en cada etapa por las preferencias sobre las soluciones presentadas.
Dentro del abanico de métodos existentes, se ha utilizado en este artículo el método AHP (Analytic Hierarchy Process) propuesto por Saaty a finales de la década de 1970, que pertenece a la categoría de los Eigenpesos y, por ello, se va a desarrollar a continuación con más profundidad (fig. 2).
El AHP calcula el autovector dominante de una matriz de comparación binaria para cada categoría y se pondera para calcular el valor normalizado que le corresponde a cada criterio.
Para ello, parte de comparar cada criterio i con cada criterio j, dos a dos, para obtener unos valores aij (aun cuando utilicen la misma notación, no tienen nada que ver con las evaluaciones de las alternativas) que se pueden agrupar en una matriz cuadrada de orden n: la llamada matriz de comparaciones binarias A = [aij]. La razón fundamental de comparar de dos en dos los criterios es que para al decisor le resulte más fácil (divide y vencerás) que compararlos todos a la vez (tabla 2).
La escala de medida elegida por Saaty para realizar las comparaciones es la mostrada en la tabla 1. En el caso de que al hacer la comparación no fuese el criterio i igual o más importante que el j, sino al revés, lo que se haría sería estimar aji; de acuerdo con lo anterior y la valoración de aij = 1/ aji.
Las matrices A de comparaciones binarias son del tipo de las llamadas matrices recíprocas, las cuales gozan de unas interesantes propiedades en las que se basa, en gran parte, la eficacia del método AHP.
Para calcular los pesos y la importancia de cada una de las alternativas en los diferentes criterios, y de los diferentes criterios entre sí, se deben obtener los vectores propios asociados al mayor valor propio de cada matriz de comparaciones binarias.
El cálculo exacto del mayor valor propio y del vector propio asociado a cada una de estas matrices, cuando las dimensiones de las matrices son mayores de 4 × 4, es muy complejo y se recurre bien a programas informáticos (Macros en MS Excel, Matlab, MDwin, Expert Choice, etc.) o en su defecto a métodos para el cálculo aproximado más inmediatos y muy fiables.
Para este caso de análisis en este artículo, de todos los métodos presentados se han utilizado los siguientes: suma ponderada, raíz n-enésima, entropía y AHP.
A continuación, se explica su fundamento teórico para poder entender su funcionamiento y características.
Suma ponderada
El método de aproximación básico consiste en sumar los elementos de cada fila y los normaliza dividiendo cada una de estas sumas entre la suma de las de todas las filas. El vector resultante es el que se use como vector de pesos.
Raiz enésima
El método de aproximación mejor consiste en multiplicar los elementos de cada fila y se hace la raíz n-ésima. Después se normalizan los resultados. El vector resultante es el que se use como vector de pesos.
Entropia
Se parte de la matriz de decisión normalizada aij, siendo i las alternativas y j los criterios para calcular la entropía Ej de cada criterio j:
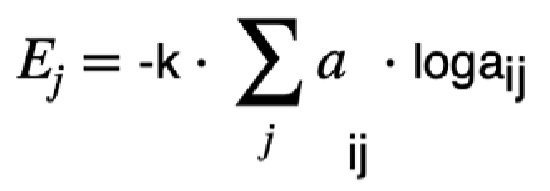 Donde k es una constante que se ajustará para que 0 FORMULA para todos los criterios. Asignando a k el siguiente valor: k = 1/log (m), m es el número de alternativas. La entropía Ej de un criterio es tanto mayor cuanto más iguales son sus evaluaciones aj;. Precisamente lo contrario de lo que nos gustaría que ocurriera si Ej fuese a ser un valor aproximado del peso del criterio. Utilizaremos, entonces, una medida opuesta que se llamará diversidad Dj del criterio: Dj =1 – Ej . Finalmente, normalizamos a suma uno las diversidades Dj y se obtienen los pesos buscados:
Donde k es una constante que se ajustará para que 0 FORMULA para todos los criterios. Asignando a k el siguiente valor: k = 1/log (m), m es el número de alternativas. La entropía Ej de un criterio es tanto mayor cuanto más iguales son sus evaluaciones aj;. Precisamente lo contrario de lo que nos gustaría que ocurriera si Ej fuese a ser un valor aproximado del peso del criterio. Utilizaremos, entonces, una medida opuesta que se llamará diversidad Dj del criterio: Dj =1 – Ej . Finalmente, normalizamos a suma uno las diversidades Dj y se obtienen los pesos buscados:
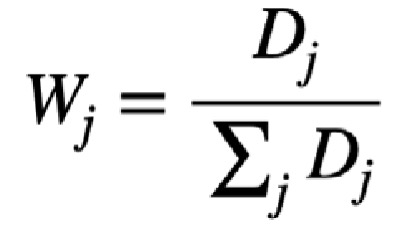 Método AHP El método AHP consiste en dividir los elementos de cada columna entre la suma de esta columna (normalizar la columna), después realizar la suma de los elementos de cada fila (ya normalizados por columnas) y dividirlos entre el número de elementos de cada fila (o sea, realizar la media) y los normaliza dividiendo cada una de estas sumas entre la suma de las de todas las filas. El vector resultante es el que se use como vector de pesos.
Método AHP El método AHP consiste en dividir los elementos de cada columna entre la suma de esta columna (normalizar la columna), después realizar la suma de los elementos de cada fila (ya normalizados por columnas) y dividirlos entre el número de elementos de cada fila (o sea, realizar la media) y los normaliza dividiendo cada una de estas sumas entre la suma de las de todas las filas. El vector resultante es el que se use como vector de pesos.
La metodología AHP con la ponderación de índices se ha utilizado en distintas publicaciones con datos de indicadores de desarrollo sostenible para las multinacionales Henkel (Krajnc y Glavic, 2004), BP y Shell (Krajnc y Glavic, 2005).
Tras realizar cualquier análisis AHP, es necesario llevar a cabo un análisis de consistencia. Una matriz de comparaciones binarias es consistente cuando aij =FORMULA , para todo i, j. Esto significa que aij (la importancia relativa de i frente a j) es exactamente el cociente wi /w j de sus pesos (sus importancias absolutas que tratamos de estimar).
Para realizar este análisis, primero se calcula AwT, multiplicando la matriz de comparaciones binaria (A) por la matriz transpuesta de los pesos (wT).
Posteriormente, se calcula el autovalor dominante de la siguiente forma:
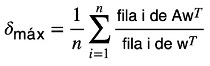 A continuación, se calcula el índice de consistencia:
A continuación, se calcula el índice de consistencia:
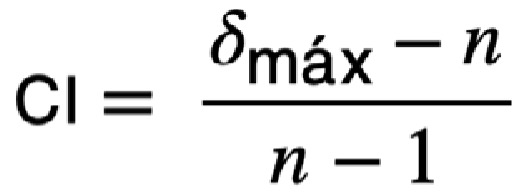 siendo n el rango de la matriz A (n x n) Para ello, hay que buscar el índice aleatorio (RI) para el rango de la matriz (N), que se establece en la tabla 3.
siendo n el rango de la matriz A (n x n) Para ello, hay que buscar el índice aleatorio (RI) para el rango de la matriz (N), que se establece en la tabla 3.
Finalmente, se hace el cociente que muestra la ratio de inconsistencia, que debe ser menor que 0,1 para que la consistencia de la matriz de comparaciones binarias sea aceptable.

2. Aplicación práctica
Tomando como referencia el trabajo realizado en 2010 por García y Báscones, en el artículo se han llevado a cabo los siguientes apartados:
Tratamiento y agregación de datos
Inicialmente se han considerado los datos obtenidos de la RCCA de referencia mencionados al inicio correspondientes al periodo comprendido entre el 15 de marzo y el 21 de junio entre los años 2016 y 2023. Este histórico de datos por contaminante, por estación de medida y por día se han descargado de la base de datos en formato MS Excel de la RCCA.
Esta información corresponde al periodo seleccionado que incluye 99 días por cada año, 10 contaminantes y 7 estaciones de medida. Una vez descargados los valores de los parámetros, más de 50.000 datos porque no en todas las estaciones se miden todos los parámetros, se han llevado a cabo los siguientes cuatro pasos:
•Paso 1. Eliminar de los ficheros Excel los valores anómalos identificados como dato erróneo (N), dato de mantenimiento de la estación de medida (M) y dato de calibración/verificación (C).
•Paso 2. Por periodos anuales, sacar promedio de cada contaminante para cada estación de medida. Finalmente, los datos por cada año serán 33 valores, dado que ninguna de las estaciones mide todos los contaminantes.
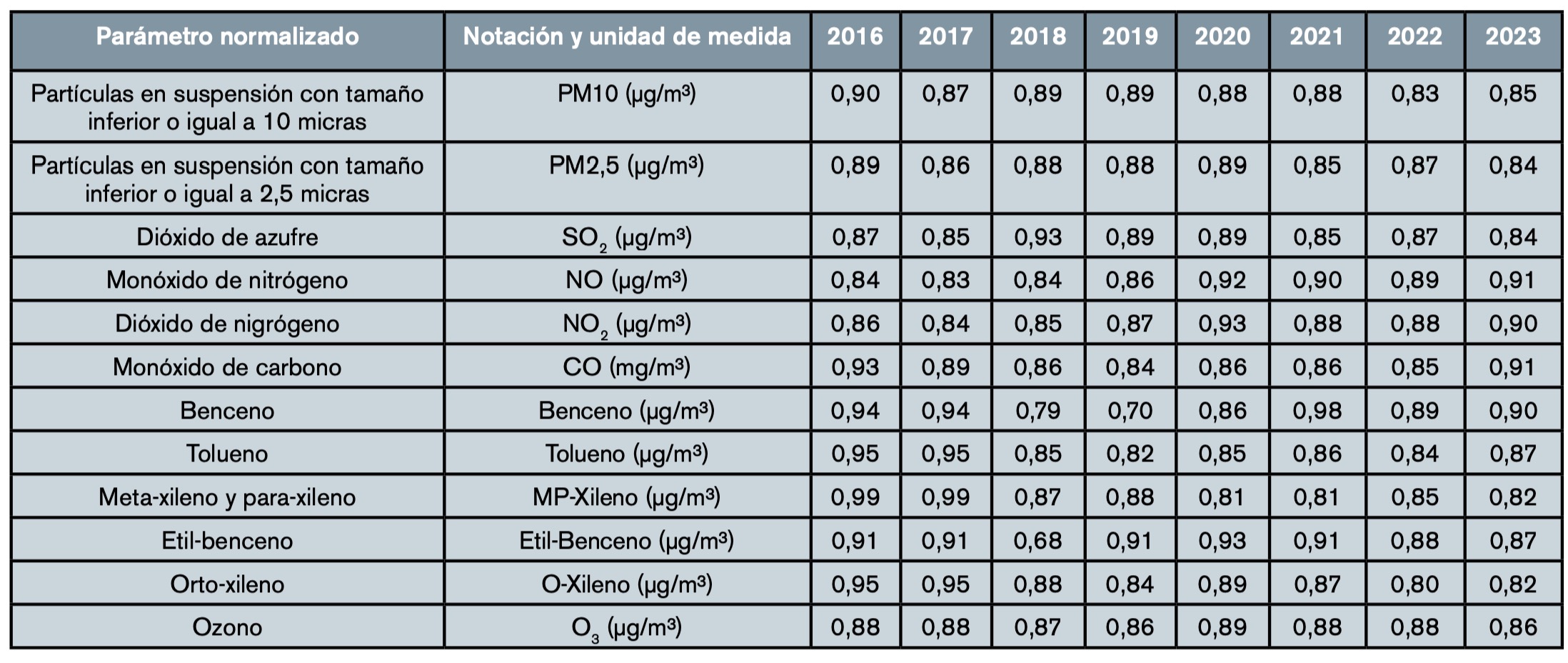
•Paso 3. Sacar promedio anual por cada contaminante. Con los valores que se han obtenido por contaminante se saca un promedio anual para cada uno de ellos. La tabla 4 es un resumen final.
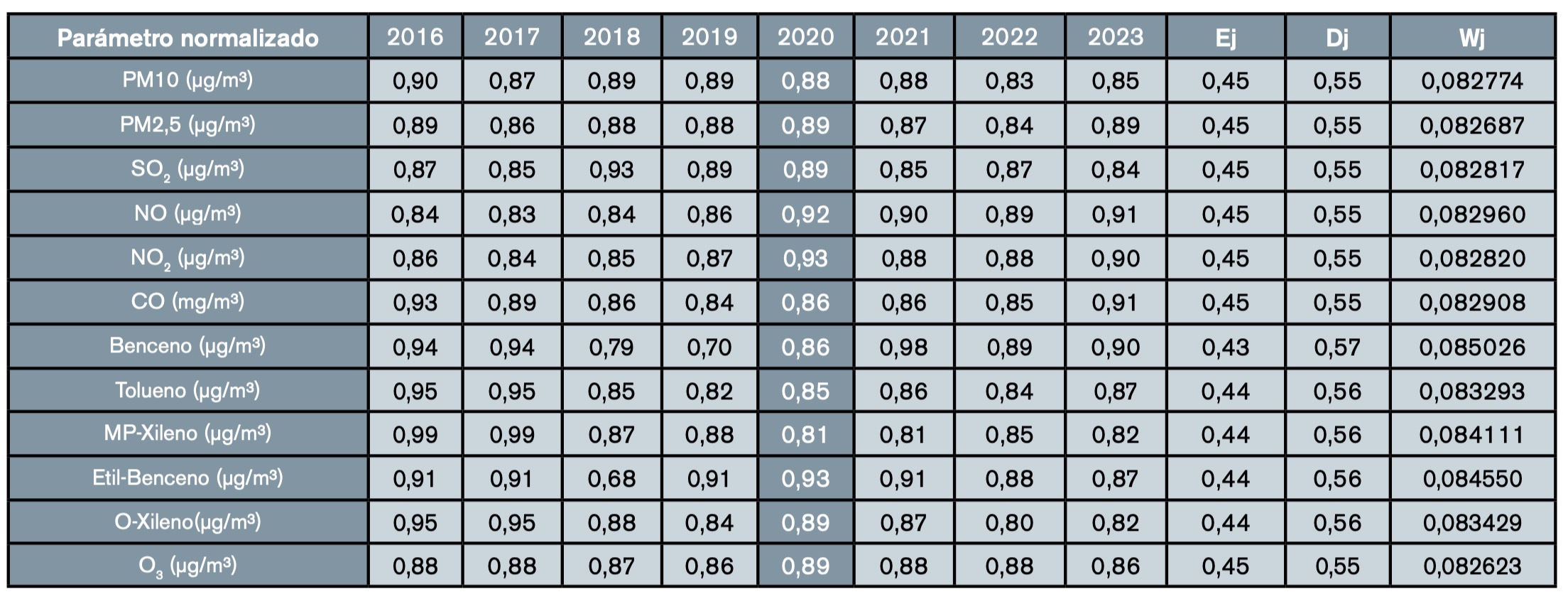
•Paso 4. Normalizar la matriz de datos. En este paso se normalizan los datos obtenidos teniendo en cuenta que todos los indicadores son decrecientes, es decir, que lo que buscamos es obtener año a año un valor lo más bajo posible. Para la normalización esto se interpreta como tender a la unidad. Cuanto más próximo esté un dato o un índice agregado a la unidad, mejor resultado será para ese parámetro medido. Para normalizar cada dato, se divide cada celda entre la suma de la fila y el valor resultante se resta de la unidad (tabla 5).


Análisis de los datos
Para la etapa de análisis de los datos, es necesario asignar los pesos a cada contaminante en función del resto y normalizar los valores. Para ello, se han llevado a cabo los siguientes dos pasos:
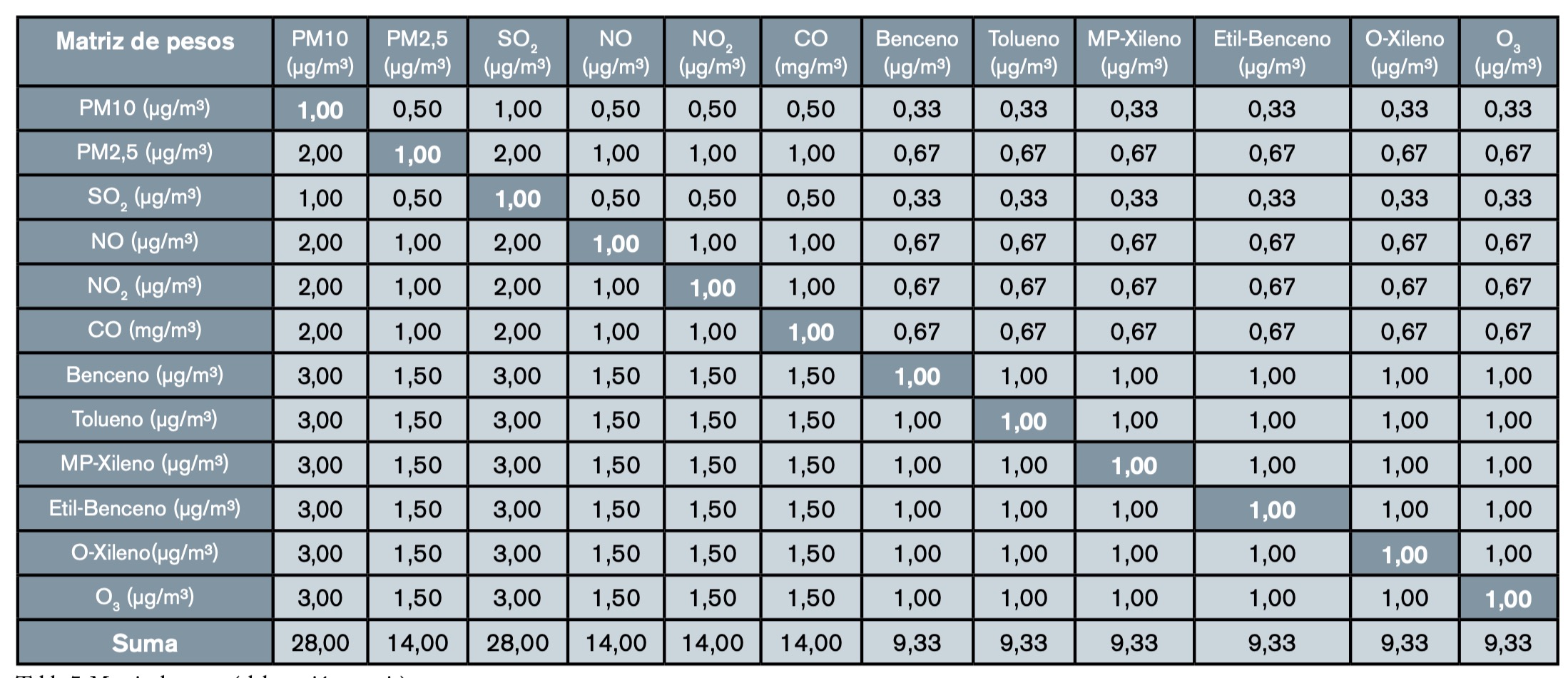
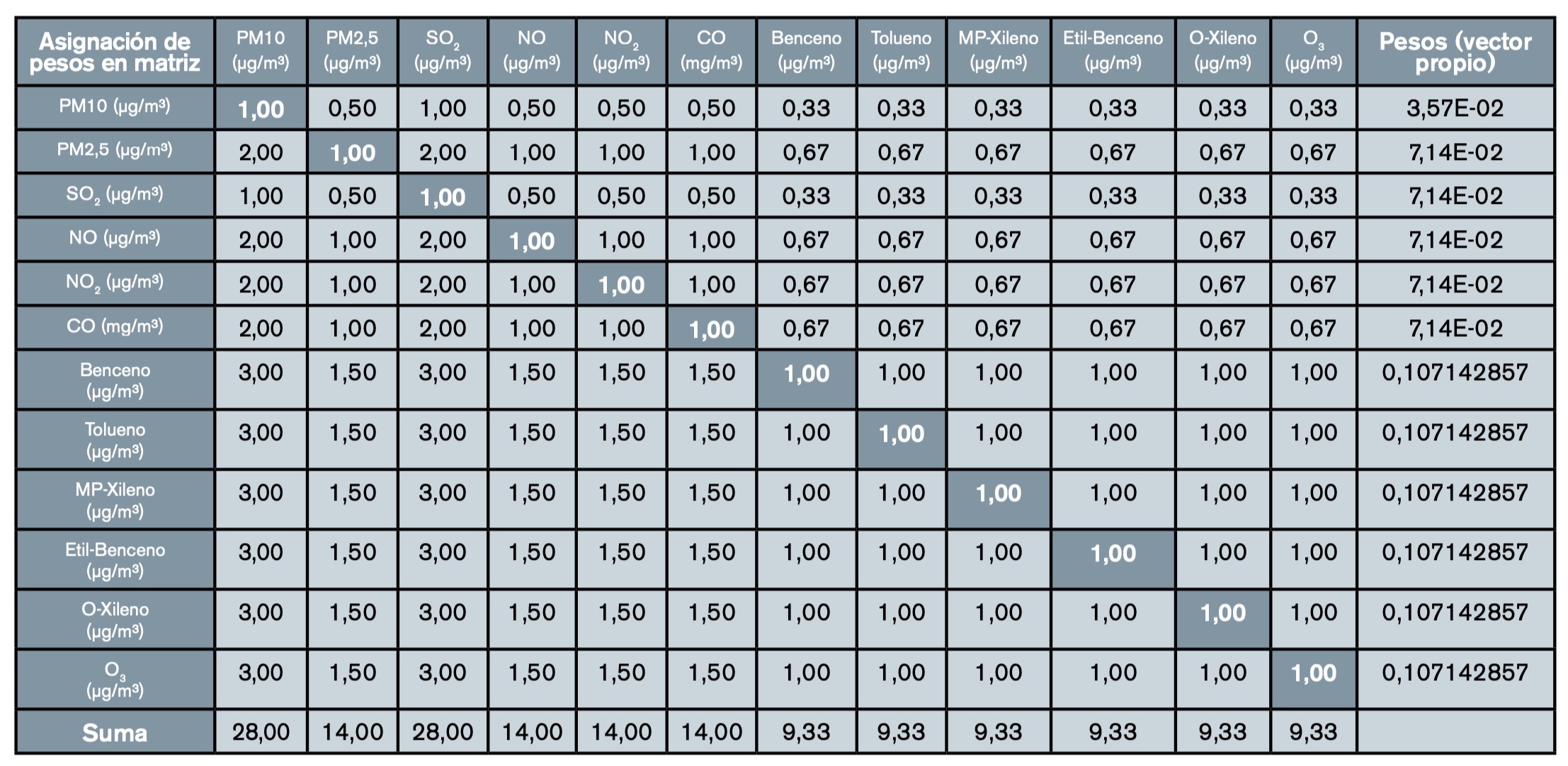
• Paso 1. Asignar los pesos a cada contaminante teniendo en cuenta entre sí su importancia en función de su nocividad y los valores límite exigidos en la legislación. A continuación, es necesario asignar los pesos en función de lo detallado en la tabla 2 para comparar la importancia relativa entre unos contaminantes y otros. Con esta asignación de pesos se construye la matriz de pesos que es clave para el correcto desarrollo del método como luego se comprobará (tabla 6). Esta asignación de pesos, que se realiza basada en la tabla 2, sirve para la elaboración de la matriz de pesos como ya hemos comentado, se trata de una matriz simétrica (tabla 7).
• Paso 2. Normalizar los resultados utilizando cuatro métodos: pesos promedio, pesos mediante la raíz enésima, pesos mediante entropía y AHP. Se comprueba consistencia de los métodos. Una vez que ya se dispone de la matriz de datos normalizada y de la matriz de pesos, se normalizan los resultados de manera global multiplicando la matriz de datos por la matriz de pesos de manera genérica. Como se van a utilizar cuatro métodos diferentes para la asignación de los pesos, en cada caso se hará de una forma diferente.
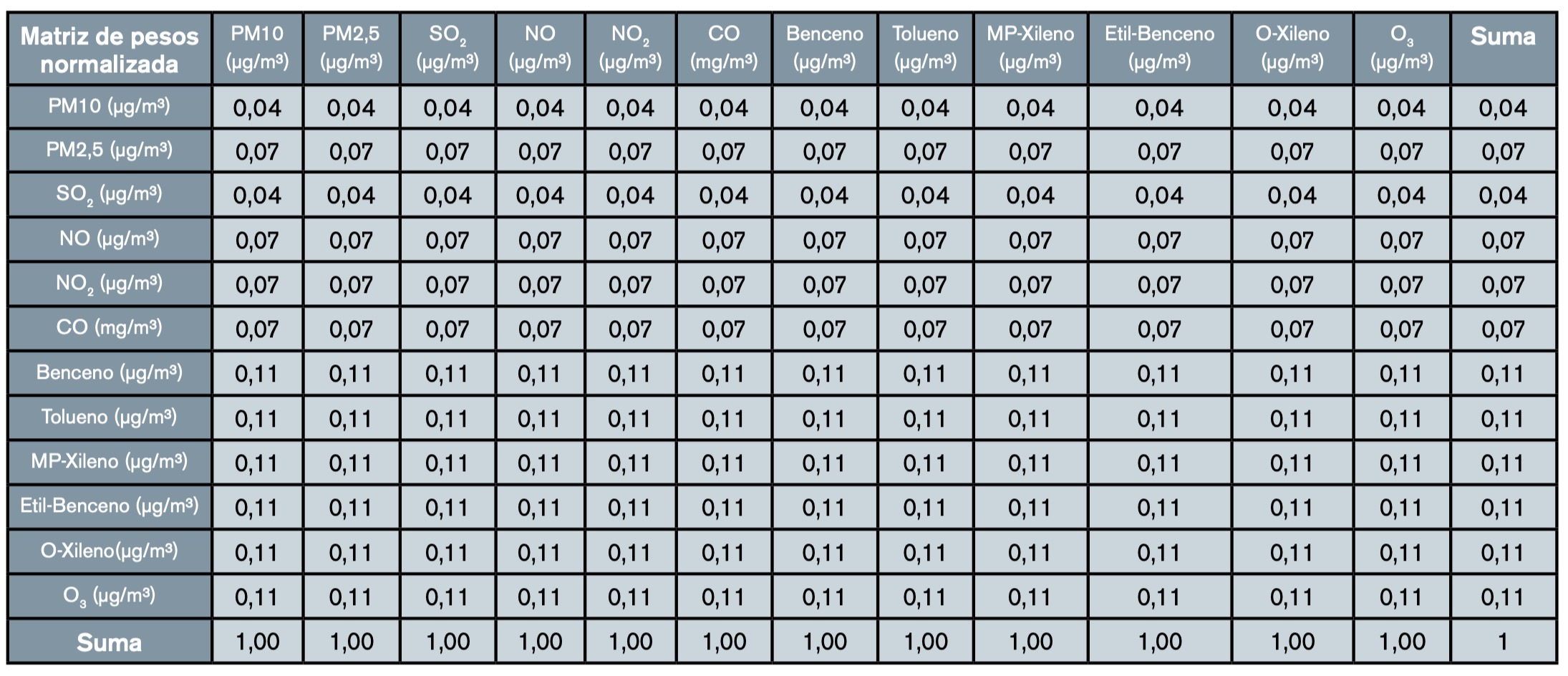
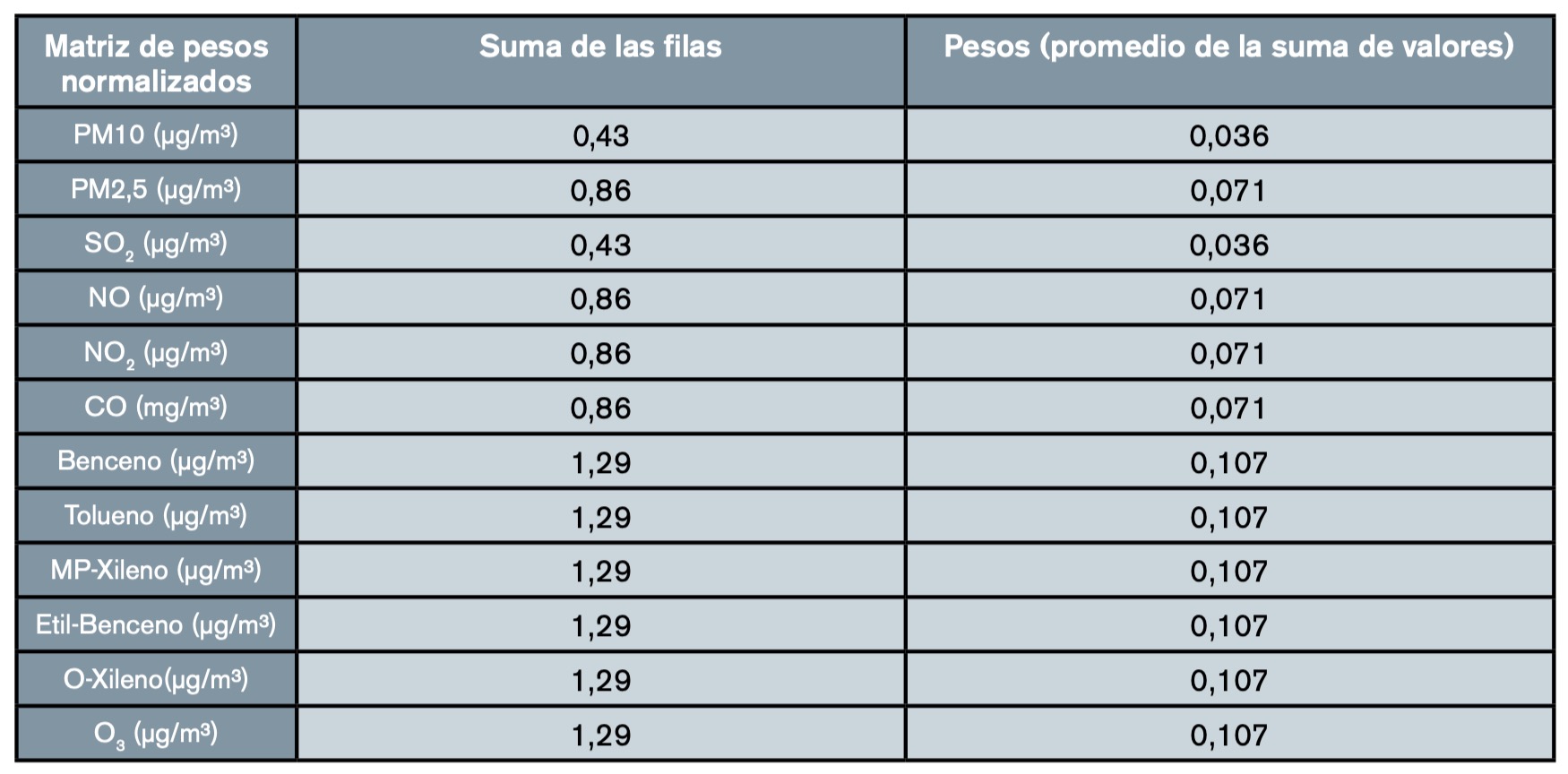
- Método 1: pesos promedio. En este método se calcula la matriz de pesos normalizada como primer paso (tabla 8).
A continuación, se multiplica de forma matricial la tabla 5 (valores promedio por contaminante y año de la RCCA normalizados) por la suma de la tabla 8 (matriz de pesos normalizada).
De esta manera, se obtienen los valores agregados de los índices por cada uno de los años usando el método de pesos ponderados, donde están representados cada uno de los 12 contaminantes de manera normalizada (tabla 9).
Al finalizar el método, se lleva a cabo el análisis de consistencia, obteniendo un CI = 0 y con un RI (12 datos) = 1,48 (tabla 3). Por tanto, el cociente CI/RI = 0; el método es consistente debido a que este número es menos de 0,1.
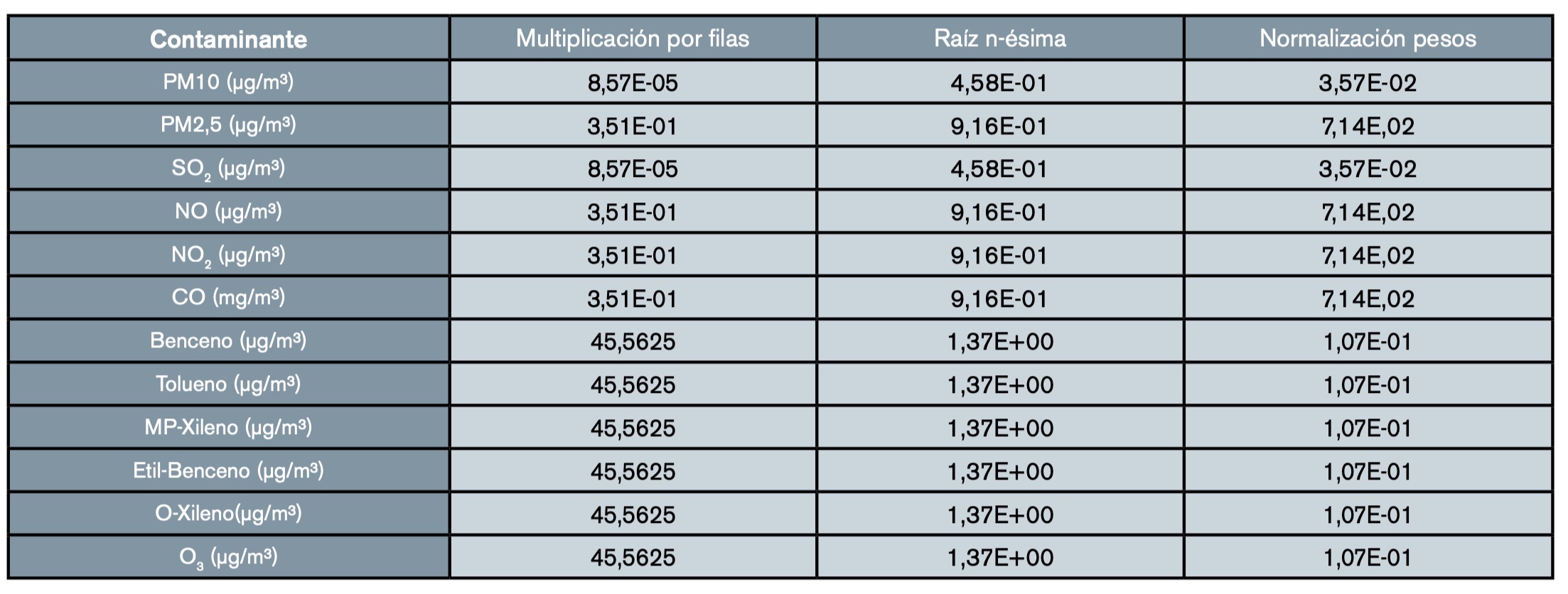
- Método 2: pesos mediante la raíz N-ésima. En este método como primer paso se hace una normalización de pesos a partir de la raíz n-ésima. Para ello, se multiplican las filas de la matriz de pesos normalizada, se calcula la raíz duodécima de estas filas y se normaliza el resultado de esta raíz (tabla 10).
A continuación, se multiplica de forma matricial la tabla 5 (valores promedio por contaminante y año de la RCCA normalizados) por la normalización de pesos de la tabla 10 (matriz de pesos normalizada a partir de la raíz n-ésima).
De esta manera, se obtienen los valores agregados de los índices por cada uno de los años usando el método de la raíz n-ésima, donde están representados cada uno de los 12 contaminantes de manera normalizada (tabla 11). Al finalizar el método, se lleva a cabo el análisis de consistencia, y se obtiene un CI = 0 y con un RI (12 datos) = 1,48 (tabla 3). Por tanto, el cociente CI/RI = 0; el método es consistente debido a que este número es menos de 0,1.
- Método 3: entropía. En este método, como primer paso se calcula la entropía Ej de cada criterio y, posteriormente, se calcula su correspondiente diversidad Dj. Finalmente, se normaliza a suma una las diversidades Dj y se obtienen los pesos buscados Wj (tabla 12).
De esta manera, se obtienen los valores agregados de los índices por cada uno de los años usando el método de la entropía, en el que están representados cada uno de los 12 contaminantes de manera normalizada (tabla 13). Este método no es susceptible del cálculo de consistencia, dado que la matriz no es simétrica.
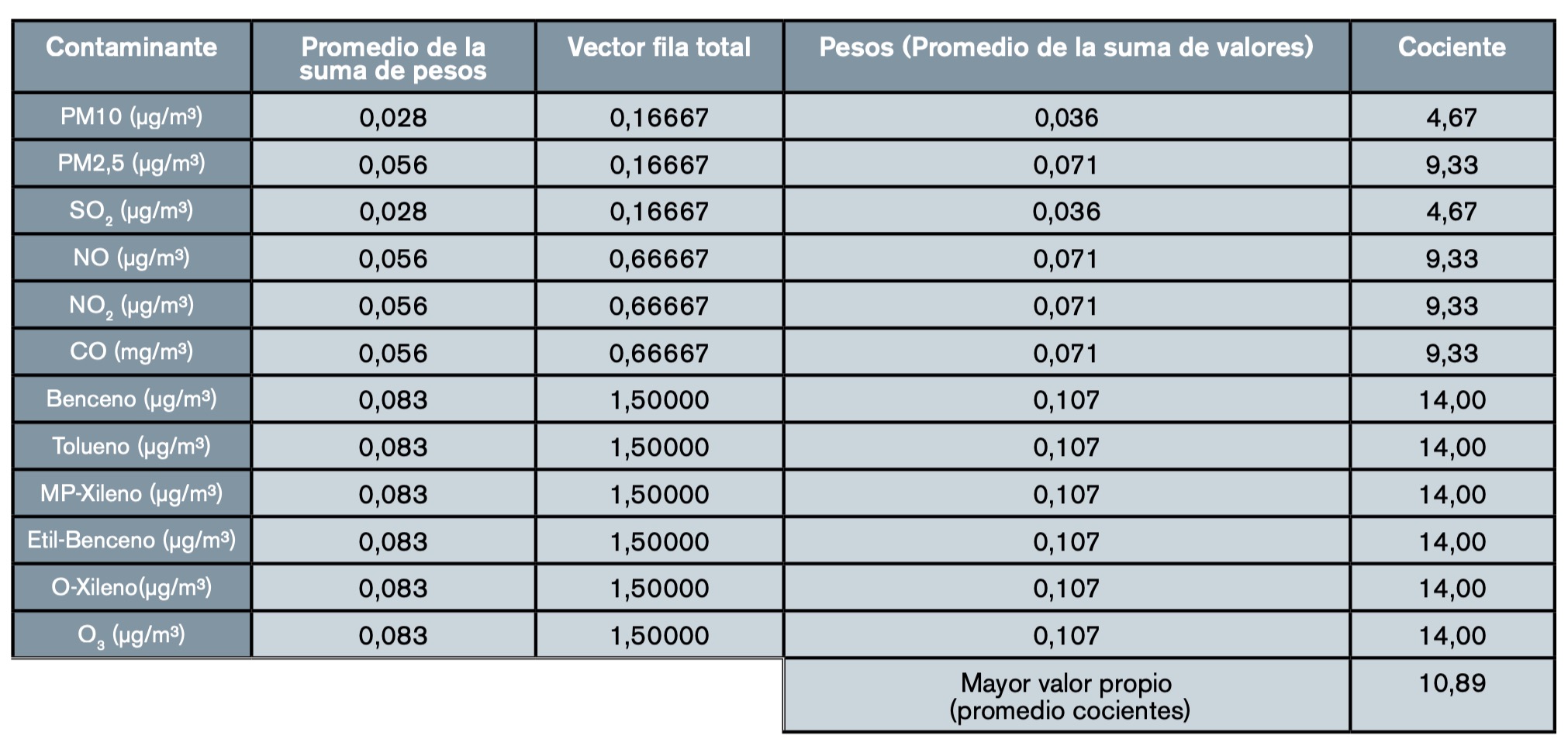
- Método 4: AHP. Para la obtención de los pesos, en este caso se ha utilizado el método AHP o de las jerarquías analíticas de Saaty, que consiste en dividir los elementos de cada columna entre la suma de esta columna (normalizar la columna). Después, se realiza la suma de los elementos de cada fila (ya normalizados por columnas) y se dividen entre el número de elementos de cada fila (o sea, se realiza la media) y se normalizan al dividir cada una de estas sumas entre la suma de las de todas las filas. El vector resultante es el que se use como vector de pesos (tablas 14-16). Con el cálculo del mayor valor propio se lleva a cabo el análisis de consistencia y se obtiene un CI = – 0,1 con un RI (12 datos) = 1,48 (tabla 3). Por tanto, el cociente CI/RI = – 0,1; el método es consistente debido a que este número es menos de 0,1. De esta manera, se obtienen los valores agregados de los índices por cada uno de los años usando el método AHP, en el que están representados cada uno de los 12 contaminantes de manera normalizada (tabla 17).


Resultados objetivos
Finalmente, el último paso es establecer una clasificación de los índices para poder concluir el año más sostenible o, lo que es lo mismo, menos contaminante.
Una vez que se tienen los valores anuales normalizados y son validados por cada método, se comparan de mayor a menor. El resultado más alto es el año con mejor perfil ambiental o, lo que es lo mismo, con menor porcentaje global de contaminantes.
Para ello, se calcula el promedio de los resultados de los cuatro métodos utilizados previamente (tabla 19). Atendiendo a los resultados promedio de los cuatro métodos, la clasificación de sostenibilidad sería la siguiente (tabla 19).


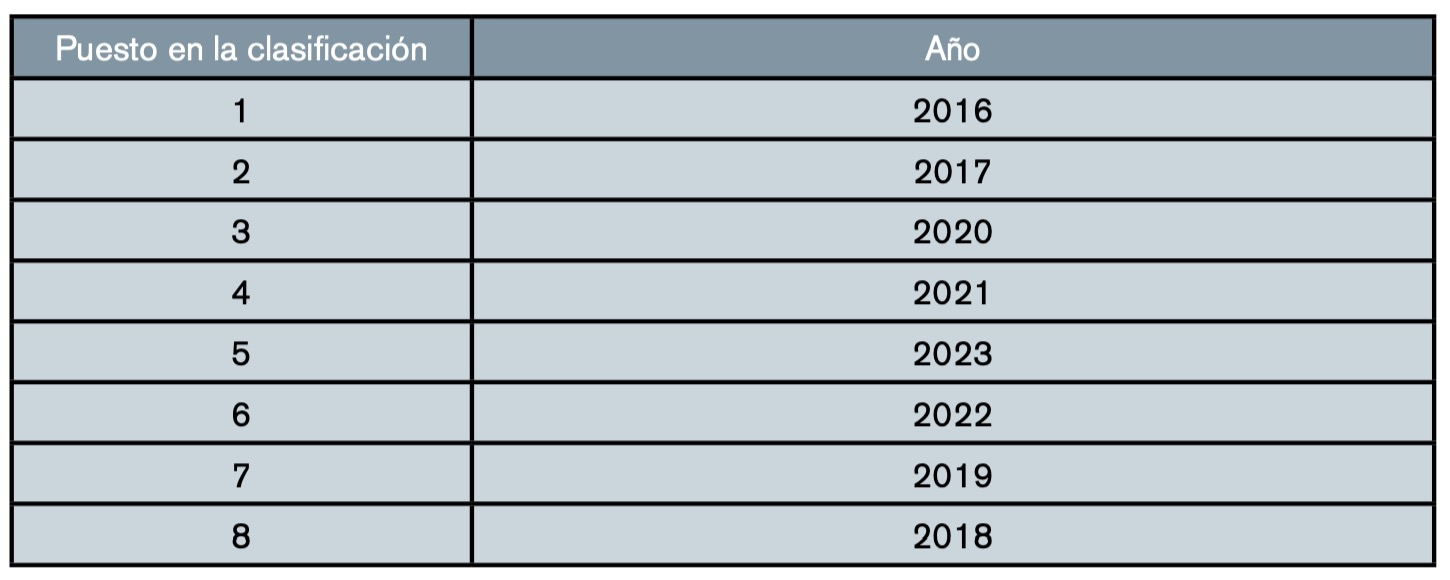
(elaboración propia).
Conclusiones
Una vez que se han analizado los datos de la RCCA para los diferentes años, las conclusiones que se obtienen son las siguientes:
• Los métodos de ayuda a la toma de decisión permiten analizar series temporales de datos para establecer una lista, dado que los valores están normalizados y ponderados, lo que comprueba la robustez del estudio.
• Los cuatro métodos de ayuda a la toma de decisión utilizados arrojan resultados similares, por lo que el análisis es robusto.
• El método de la entropía es el único que aporta resultados algo diferentes; los valores de los otros tres métodos son exactamente iguales, a pesar de tener fundamentos matemáticos diferentes.
• Según la tabla 19, se concluye lo siguiente:
– En contra de lo que inicialmente pudiera parecer, el periodo correspondiente al año 2016 es el más sostenible, dado que su índice agregado es el mayor de todos.
– El periodo del año 2020 (periodo del estado de alarma) es el tercero en la clasificación. Analizando los parámetros y comparándolos con otros años, se detectan valores bajos para el dióxido de azufre, monóxido de nitrógeno y dióxido de nitrógeno. En cambio, los parámetros de hidrocarburos policíclicos aromáticos y de ozono que pesan más en el análisis son medios-altos. –
El periodo del año 2018 es el menos sostenible, dado que su índice agregado es el menor de todos.
Bibliografía
Álvarez-Arenas, M. (2000): “Indicadores del Desarrollo Sostenible”. Ekonomi Gerizan. Nº 7: 114-131, Federación de Cajas de ahorros Vasco-Navarras, Bilbao.
Chiavenato, A. (2007): “Administración de Recursos Humanos”. McGraw-Hill Interamericana, Colombia.
García Vílchez, E.J., Sánchez Báscones, M.I. (2010): “Desarrollo del modelo de sostenibilidad integrado (M.S.I.) para la medida de la gestión sostenible de una industria de procesos: Aplicación al sector de fabricación de neumáticos”. Universidad de Valladolid (España). Y/D Tesis 003933
Keeney, R. L. (1982): “Decision analysis. An Overview”. Woodward-Clyde Consultans. San Francisco (California). doi:10.1057/jors.1982.89
Krajnc, D., Glavic, P. (2004): “A model for integrated assessment of Sustainable Development”. Resources, Conservation and Recycling. Vol. 43, nº 2:189-208, Elsevier Ltd.
Krajnc, D., Glavic, P. (2005): “How to compare companies on relevant dimensions of sustainability”. Ecological Economics. Vol. 55, nº 4: 551-553. Elsevier Ltd.
Quijano, A, Orozco, J.A. (2005): “ Monitoreo de material particulado-fracción respirable (PM2,5) en Pamplona (Colombia)”. Revista de la Facultad de Ciencias Básicas. Vol. 3, nº. 2: 1-11.
Saaty, T.L. (1980): “The Analytic Hierarchy Process”. McGraw-Hill, New York.
Saaty, T.L. (1982): “Decision making with the analytic hierarchy process”. International Journal of Services Sciences. Vol.1, nº 1:83-98, Pittsburgh (Pensilvania).
Simon, H. (1960): “The new Science of Management Decision”. Harper & Row, New York.
Venkata Rao, R. (2007): “Decision making in the manufacturing environment. Using graph theory and fuzzy multi attribute decision making”. Springer-Verlag, London.
Web del Ayuntamiento de Valladolid (https://www.valladolid.es/es/rccava). Consultada entre el 01/02/2023 y el 31/07/2023.

