Diseño y validación de un controlador predictivo no lineal basado en un modelo aplicado al seguimiento de trayectorias de vehículos autónomos

Marc Sánchez-Mateu1, Daniel S. Gamba2, J Pérez-Fernández2, JA Cabrera Carrillo2, JJ Castillo-Aguilar2

 

Resumen

El campo de los vehículos y de la conducción autónoma se encuentra inmerso en un rápido crecimiento y expansión. Por ello, en el presente artículo se pretende diseñar un controlador predictivo que sea capaz de calcular el ángulo de dirección óptimo para poder seguir una trayectoria genérica, además de realizar trayectorias como el cambio de carril y el doble cambio de carril. Este tipo de controladores necesita un modelo interno que represente la dinámica longitudinal, lateral y la guiñada con precisión, el cual se describe mediante un conjunto de ecuaciones diferenciales de segundo orden que especifica dicho comportamiento dinámico. A diferencia de otros tipos de controladores, el controlador predictivo requiere de la resolución de un problema de optimización para obtener la acción de control. La función de coste característica de la optimización se compone de un conjunto de matrices que, en su totalidad, describen el comportamiento del controlador predictivo. Se destaca la importancia de recoger el comportamiento dinámico del modelo en su forma matricial. Para ello, se debe someter al conjunto de ecuaciones diferenciales a un proceso matemático de linealización, obteniendo la representación en espacio de estados del modelo. Una vez representado en su forma matricial, se construyen el resto de matrices de la optimización a partir de estas. En la resolución del problema de seguimiento de trayectorias, es habitual el uso de modelos de vehículo simplificados que asumen un comportamiento del neumático lineal, en el que las fuerzas laterales y longitudinales de estos son proporcionales al ángulo de deriva.

Palabras clave: Control predictivo basado en un modelo no lineal (NMPC), control predictivo basado en modelo (MPC), seguimiento de trayectorias (PT) y programación cuadrática (QP).

 

Abstract

The field of vehicles and autonomous driving is currently undergoing rapid growth and expansion. For this reason, the present article aims to design a predictive controller capable of calculating the optimal steering angle to follow a generic trajectory, as well as to perform manoeuvres such as lane changes or double lane changes. This type of controller requires an internal model that accurately represents the longitudinal, lateral, and yaw dynamics, which is described by a set of second-order differential equations that capture such dynamic behaviour. Unlike other types of controllers, the predictive controller requires solving an optimization problem to obtain the control action. The cost function characteristic of the optimization is composed of a set of matrices that, as a whole, describe the behaviour of the predictive controller. Emphasis is placed on capturing the dynamic behaviour of the model in its matrix form. To achieve this, the set of differential equations must undergo a mathematical linearization process, resulting in the state-space representation of the model. Once expressed in its matrix form, the remaining optimization matrices are derived from it. In solving the trajectory tracking problem, it is common to use simplified vehicle models that assume linear tire behaviour, in which lateral and longitudinal forces are proportional to the slip angle.

Keywords: Nonlinear model predictive control (NMPC), model predictive control (MPC), path tracking (PT), quadratic programming (QP).

---

Recibido/received: 03/07/2025

Aceptado/accepted: 27/09/2025

1Departamento de ingeniería Mecánica, Universidad de Málaga; e-mail: ma*********@*ma.es

2Departamento de ingeniería Mecánica, Universidad de Málaga; e-mails: da*********@*ma.es, ja*********@*ma.es, jc******@*ma.es, ju*****@*ma.es

 

---

INTRODUCCIÓN

Debido al incremento de la congestión del tráfico y al aumento de incidentes causados por una conducción impropia, el interés por la implantación del vehículo autónomo en la sociedad actual se ha visto incrementado. En los últimos años, ha surgido un avance tecnológico en el campo de la conducción autónoma impulsado por su potencial para mejorar la seguridad, promover una conducción eficiente en el consumo de energía y optimizar el flujo del tráfico (Urmoson et al.). Es por ello por lo que Qing Li analiza las necesidades del vehículo autónomo y presenta la arquitectura del sistema de control y la capacidad de detectar carriles de forma automática (Li et al., 2004). Desde entonces, muchos investigadores han dedicado grandes esfuerzos a realizar avances en el desarrollo y el control del vehículo autónomo. Desde la perspectiva de la detección de obstáculos, Häne es capaz de extraer la información de obstáculos estáticos de mapas de profundidad calculados a partir de imágenes consecutivas (Häne et al., s.f.). Abdelmoghit Zaarane plantea un sistema de medición de distancia entre vehículos para conducción autónoma basado en el procesamiento de imágenes, haciendo uso de cámaras estéreo y procesamiento de imagen (Zaarane et al., 2020). Desde la perspectiva del path planning, Huang propone el uso de un algoritmo RRT (Rapidly-exploring Random Tree) para la planificación de rutas en un entorno complejo con un gran número de obstáculos aleatorios (Huang & Ma, 2022). Chao Chun Yuan presenta un nuevo algoritmo de fusión que combina el algoritmo de colonia de hormigas y un campo potencial mejorado, lo que permite que el vehículo autónomo evite obstáculos y conduzca de manera más segura (Yuan et al., 2020).

En el área del control de vehículos autónomos, José E. Naranjo propone un sistema de adelantamiento para vehículos autónomos equipado con capacidades de seguimiento de trayectoria y cambio de carril. El sistema utiliza controladores difusos que imitan el comportamiento y las reacciones humanas durante maniobras de adelantamiento; se basa en la información proporcionada por un sistema de posicionamiento global de gran precisión y un entorno de red inalámbrica (Naranjo et al., 2008). Hamid presenta un novedoso método de control indirecto robusto y adaptativo basado en un enfoque de red neuronal difusa de tipo 2 con modo deslizante de tipo exponencial, considerando incertidumbres paramétricas relacionadas con la rigidez nominal en curva del vehículo, el coeficiente de adherencia neumático-carretera, los parámetros inerciales y la velocidad de avance (Taghavifar & Rakheja, 2019). Teniendo en cuenta el conflicto existente entre precisión de seguimiento y la estabilidad bajo condiciones extremas de conducción, Tchamna promueve un nuevo enfoque para controlar la tasa de guiñada y el deslizamiento lateral de un vehículo, sin descuidar su dinámica longitudinal y sin realizar suposiciones simplificadoras sobre su movimiento (Tchamna y Youn, 2013). Kibeom Lee propone un control lineal cuadrático gaussiano (LQG) para diseñar de manera eficiente y sistemática el controlador de seguimiento de trayectoria, al mismo tiempo que maneja eficazmente los problemas de ruido y error que surgen de los algoritmos de localización y planificación de trayectorias (Lee et al., 2019). Hay multitud de técnicas y algoritmos para realizar el control sobre el movimiento del vehículo, pero todos están enfocados en mejorar la precisión y la estabilidad del control. Más allá de estos controladores, el control predictivo basado en modelo destaca por su capacidad para manejar sistemas complejos y dinámicos, optimizando el control mientras respeta las restricciones operativas del vehículo (Yu et al., 2021), convirtiéndolo en el algoritmo de control más empleado a la hora de resolver los problemas de seguimiento de trayectorias en vehículos autónomos.

Primeramente, Falcone (2007) defiende la implementación de un controlador predictivo para controlar un sistema de dirección activa en el eje delantero de un vehículo autónomo. Este compara dos enfoques con diferentes costes computacionales: el uso de un modelo no lineal de elevada complejidad del vehículo, sujeto a un proceso de linealización en cada iteración, y un modelo de menor complejidad cuyos parámetros varían de forma lineal. Este último tiene en cuenta el estado del vehículo y las restricciones para garantizar la estabilidad a grandes velocidades y en superficies con poca adherencia. Posteriormente, Falcone et al. (2008) presentan un esquema de seguimiento de trayectoria basado en control predictivo por modelo (MPC) para realizar maniobras de evasión de obstáculos mediante la optimización del ángulo de la dirección y el control de la aceleración o el frenado. Cheng (2021) diseña un controlador de seguimiento de trayectoria robusto basado en MPC, capaz de hacer frente a incertidumbres en los parámetros. Este controlador incorpora un algoritmo novedoso que puede resolverse mediante un conjunto de desigualdades matriciales lineales (LMI), derivadas del principio de estabilidad asintótica de Lyapunov. Más tarde, Cheng et al. (2021) proponen un algoritmo de control predictivo adaptativo, el cual calcula los parámetros característicos del controlador en función del estado del vehículo y de las condiciones del trazado. En la mayoría de los artículos previamente citados, muchos autores optan por emplear el modelo lineal de bicicleta, el cual ayuda a reducir el coste computacional y muestra gran precisión siempre y cuando se trabaje en la zona lineal del neumático. Sin embargo, en maniobras extremas y en superficies de baja adherencia, este controlador presenta limitaciones. Por ello, en el presente artículo se diseña un algoritmo de control predictivo basado en el modelo no lineal de Dugoff, el cual, mediante una formulación matemática más simple que otros modelos de neumático como el de Pacjecka, puede reproducir con precisión el comportamiento real del neumático.

 

MODELO DINÁMICO DEL VEHÍCULO

Modelo de bicicleta

La resolución del problema de seguimiento de trayectorias (PT) depende en gran medida del modelo de vehículo empleado, ya que es un requisito indispensable para la estrategia de control utilizada. Los vehículos son sistemas muy complejos, con múltiples grados de libertad y una gran cantidad de parámetros que varían de forma no lineal con el tiempo. Debido a esta complejidad, resulta extremadamente difícil desarrollar un modelo capaz de capturar, en su totalidad, todas las características del vehículo. Además, emplear un modelo tan detallado implicaría un aumento significativo en el costo computacional, lo que dificultaría su implementación en el control en tiempo real. Por ello, es esencial utilizar un modelo dinámico simplificado cuyos parámetros puedan adaptarse con el tiempo, manteniendo un equilibrio entre precisión y viabilidad computacional. Este enfoque permite un buen seguimiento de la trayectoria en tiempo real sin comprometer el rendimiento.

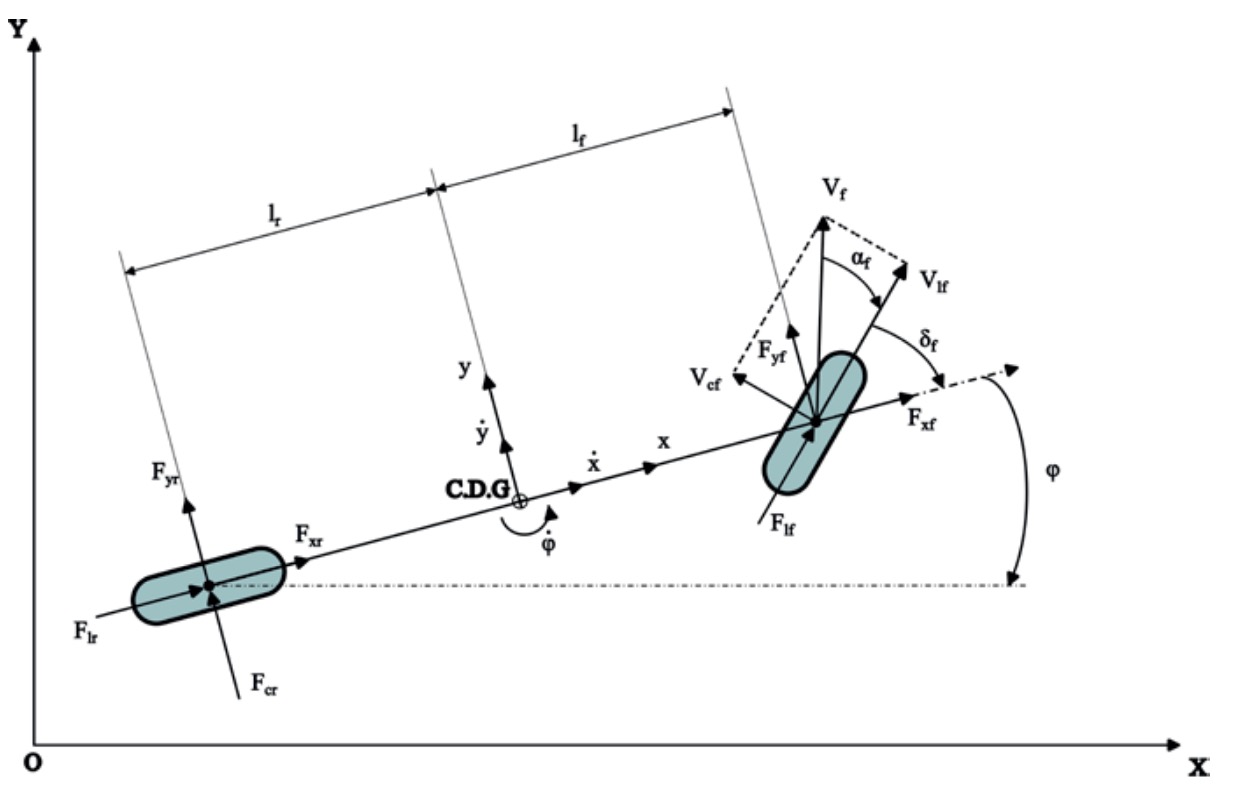
En este apartado, se introduce el modelo de vehículo y de neumático empleado para el control basado en el espacio de estados. Dicho modelo debe ser capaz de describir la dinámica plana del automóvil, y es necesario describir mediante ecuaciones los movimientos longitudinales, laterales y de rotación. Se selecciona el modelo de bicicleta con tres grados de libertad para modelizar la dinámica plana de vehículos sin considerar la geometría de Ackerman. Este es una representación simple y efectiva que se utiliza ampliamente en los controles de estabilidad y trayectoria de vehículos autónomos (Lin, Sun, Wu, y Qian, 2021). Este artículo demuestra cómo aplicando dicho modelo simplificado, que incluye la rigidez de los neumáticos, puede lograrse un seguimiento preciso y suave de la trayectoria de referencia. El modelo es eficaz incluso en condiciones difíciles que involucran movimientos laterales, longitudinales y de giro del vehículo. Para poder aplicar este modelo, se deben considerar las siguientes simplificaciones:

•Las ruedas del mismo eje se agrupan en una sola rueda ubicada en el centro del eje delantero o trasero.

•El peso del cuerpo del vehículo se distribuye en cada rueda.

•Efectos como los movimientos de la suspensión, fenómeno de deslizamiento y los efectos de la aerodinámica son despreciados.

•Se ignoran efectos como la relación de acoplamiento de la fuerza del neumático y el efecto del par de alineación.

La representación del modelo en un sistema de coordenadas plano puede visualizarse en la figura 1.

De acuerdo con la Segunda Ley de Newton y Euler, el equilibrio de fuerzas y momentos resultante a lo largo de los ejes x, y y z locales cuya referencia está centrada en el centro de gravedad del vehículo es el siguiente:

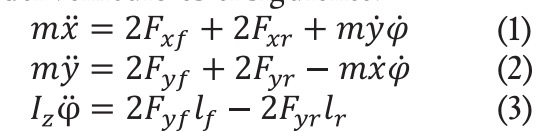donde m es la masa del vehículo, y son las fuerzas longitudinales de las ruedas delantera y trasera respecto del eje local x. y son las fuerzas laterales sobre los delantero y trasero, calculadas respecto del eje local y. La inercia del vehículo respecto del eje z viene representada por el parámetro .

Las fuerzas de los neumáticos delantero y trasero obtenidas en las direcciones x e y se relacionan con las fuerzas longitudinales y laterales de estos. La relación es la siguiente [1]:

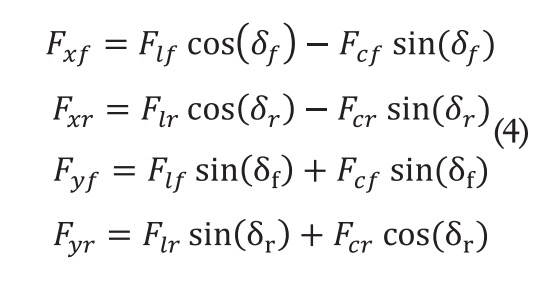En la fórmula (4), y son las fuerzas longitudinales de las ruedas delantera y trasera, y son las fuerzas laterales de ambas ruedas (delantera y trasera). Los ángulos de dirección delantero y trasero se representan como y respectivamente. Se asume que el modelo de vehículo seleccionado solo tiene dirección en la rueda delantera, lo que resulta en que =0. Además, si se desprecia el efecto de transferencia de carga y asumiendo que la velocidad del vehículo cambia lentamente, las cargas verticales del neumático delantero y trasero puede calcularse (Chen et al., 2013):

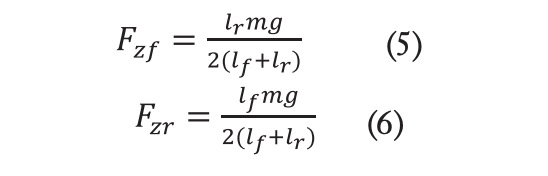
Las fuerzas longitudinal y lateral del neumático puede expresarse como una función compleja del ángulo de deriva del neumático ángulo de deslizamiento longitudinal del neumático s y la fuerza vertical , además de otros parámetros que se comentarán con más detalle posteriormente:

Además, los ángulos de deriva trasero y delantero pueden calcularse aplicando la siguiente ecuación:

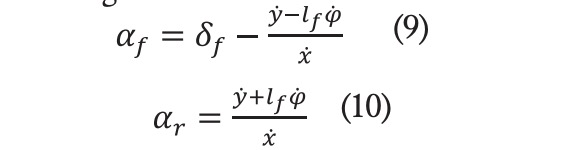En la fórmula, y son los ángulos de deslizamiento de las ruedas delanteras y traseras, respectivamente, e son las velocidades longitudinal y lateral del vehículo, es la tasa de variación del ángulo de guiñada y , el ángulo de dirección de la rueda delantera. Con el fin de minimizar el coste computacional para el modelo simplificado, se asume la hipótesis de pequeños ángulos de deslizamiento. Se traduce en una simplificación en las funciones trigonométricas que aparecen en las ecuaciones que describen la dinámica del modelo de bicicleta de la figura 1. Se da la siguiente condición: (11)

Las ecuaciones (1)-(8) derivan del sistema de coordenadas local centrado en el cuerpo del vehículo. Hay una relación entre el sistema de coordenadas fijo en el cuerpo y el sistema de coordenadas inercial X,Y:

Donde X es la posición longitudinal en el sistema de referencias inercial e Y es la posición lateral en el sistema de coordenadas inercial.

 

Modelo de neumático no lineal.

Modelo de Dugoff.

Para conseguir una reducción en el coste computacional de los cálculos, es muy habitual encontrar algoritmos de control en los que se asume la hipótesis de pequeños ángulos de deslizamiento descrito en la ecuación (9). Cuando dicha hipótesis es cierta y los ángulos de deslizamiento longitudinal y lateral son pequeños, las fuerzas que actúan sobre el neumático pueden aproximarse linealmente como:

En la ecuación (12), es la rigidez longitudinal del neumático y es su rigidez lateral. El uso de dicha ecuación tiene limitado el rango de aplicación, ya que solo es viable su uso para aceleraciones laterales menores de 0,3-0,4 g y condiciones de adherencia normales y no cerca de la pérdida de tracción. En caso de sobrepasar el límite de la aceleración lateral o si el vehículo circula en superficies de baja adherencia, las fuerzas laterales y longitudinales que se calculan en el modelo interno del controlador pueden inducir cierto error. Empíricamente, se ha observado que, en caso de sobrepasar dichas limitaciones, el incremento de las fuerzas en el neumático es más lento con el ángulo de deriva longitudinal y lateral, perdiendo la linealidad. Por ello, las fuerzas calculadas bajo la hipótesis lineal de pequeños deslizamientos serían mayores que la fuerza bajo condiciones reales, lo que introduce una discrepancia en el modelo interno del controlador y afecta el rendimiento del controlador. Para hacer el controlador más preciso y versátil, se implementa un modelo de vehículo basado en el modelo de neumático no lineal de Dugoff (Gao et al., 2024.), reemplazando el coeficiente de rigidez constante de la ecuación (12) por un coeficiente corregido no lineal, el cual permite capturar el comportamiento real del neumático bajo condiciones que favorecen la pérdida de proporcionalidad entre el deslizamiento y la fuerza. La expresión que se usa para el cálculo de este nuevo coeficiente de rigidez no lineal es:

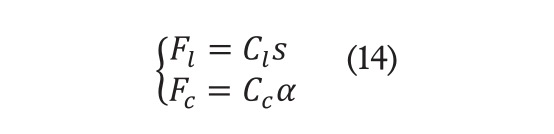
es el parámetro de deflexión del neumático, el cual otorga al modelo interno la capacidad de reproducir el comportamiento del neumático con mayor rigor, involucrando los rangos de trabajo en los que se pierde la linealidad debido a los factores descritos en el párrafo anterior. Este se calcula aplicando la siguiente fórmula:

es el coeficiente de adherencia, es la carga vertical sobre el neumático, es el valor de referencia del coeficiente de rigidez longitudinal del neumático y es el valor de referencia de rigidez lateral. y son sus ángulos de deslizamiento longitudinal y lateral. El índice i indica la dirección de la fuerza (x o y) y el índice j la rueda en la que se aplica la fuerza (delantera o trasera). En las ecuaciones, la rueda delantera se asocia con la letra f, que deriva del inglés front. Para la rueda trasera, se hace uso de la letra r, en inglés rear. Una vez calculados los parámetros de rigidez longitudinal y lateral, pueden obtenerse las fuerzas lateral y longitudinal de forma sencilla:

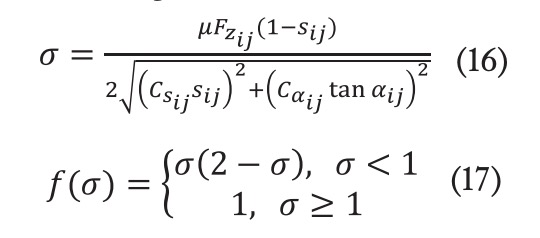
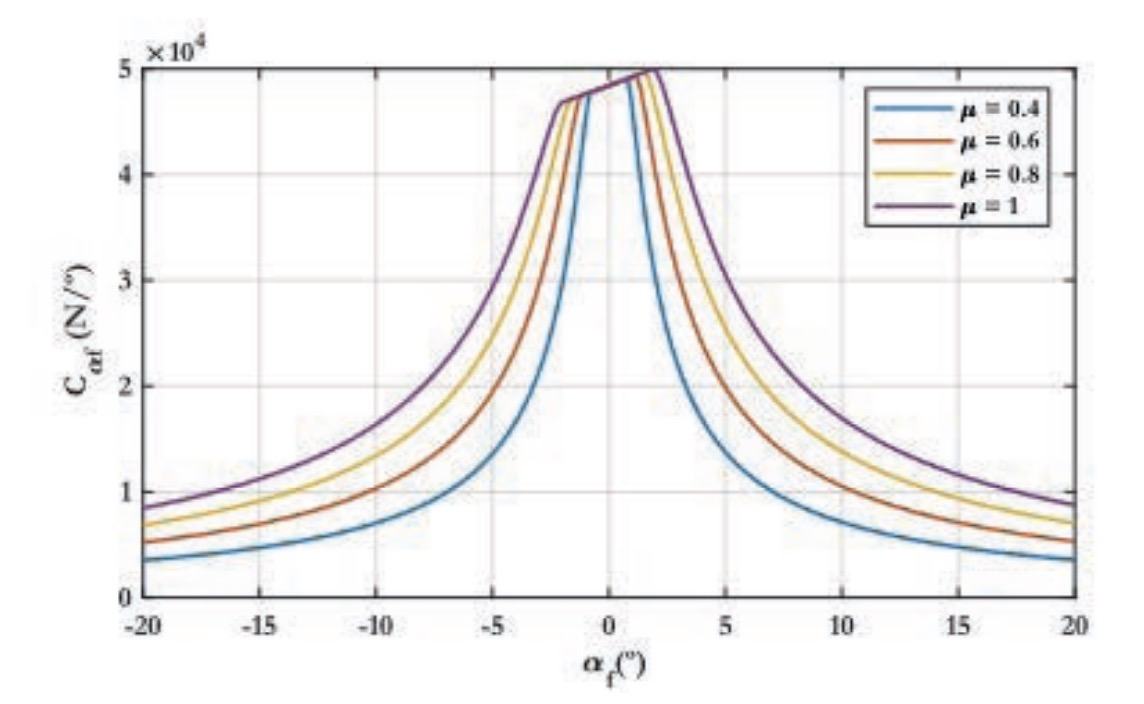
En la figura 2 puede verse la evolución del nuevo coeficiente de rigidez frente al ángulo de deslizamiento del neumático a distintos valores de coeficiente de fricción . Para ángulos de deslizamiento pequeños (0-2 grados), dicho coeficiente presenta un comportamiento lineal, lo que hace que la fuerza lateral varíe también linealmente. De este modo, se valida la hipótesis de proporcionalidad planteada inicialmente. Por otro lado, en dicha figura también se aprecia que, a partir de ángulos de deslizamiento más elevados, por encima de 2 grados aproximadamente, el valor que toma el coeficiente de rigidez propuesto disminuye de forma no lineal y captura la variación no uniforme tan característica del neumático (Gao et al., 2024.). Este cambio en la rigidez no solo refleja la capacidad del neumático para mantener la adherencia a altas velocidades o en condiciones extremas, sino también la forma en que las características del material y la estructura del neumático influyen en su rendimiento bajo diferentes condiciones de carga y deslizamiento. Bastaría con aplicar las fórmulas (18) y (19) para obtener el valor de las fuerzas longitudinal y lateral para su respectivo coeficiente de rigidez ajustado .

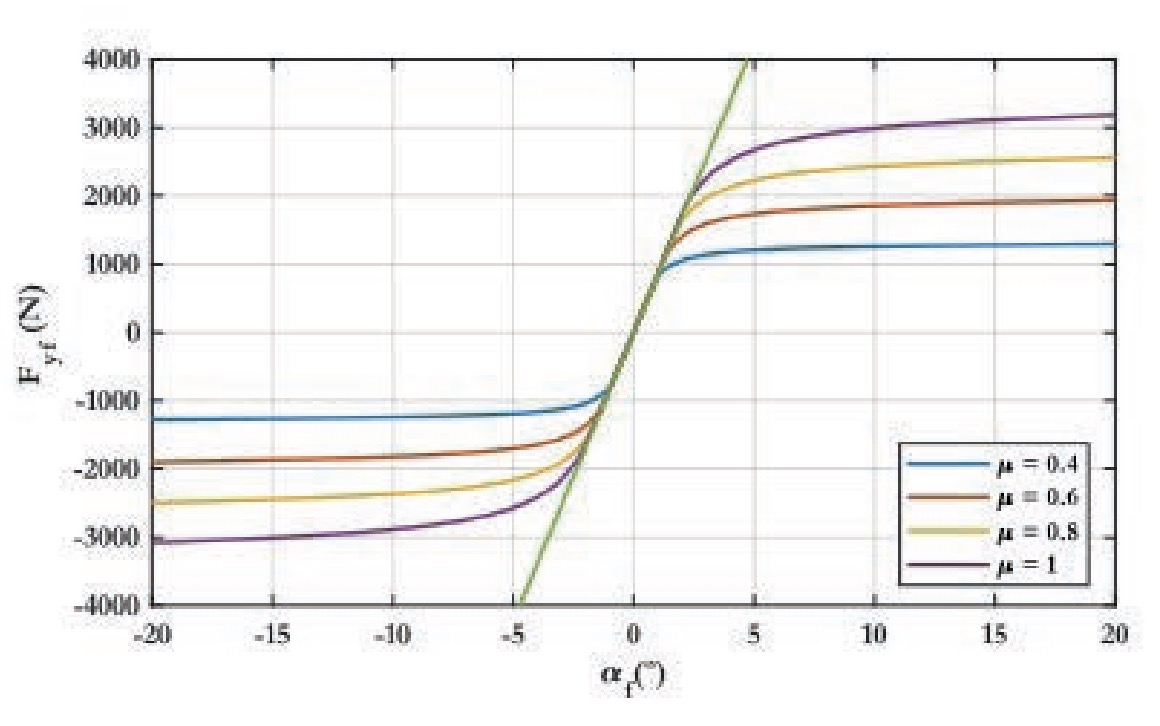
En la figura 3 puede visualizarse que, ante un determinado valor de carga vertical de 4.120 N, la influencia del coeficiente de fricción sobre las fuerzas laterales a las que se puede ver sometido el neumático. El propio valor del coeficiente de rodadura determina el límite de deslizamiento de este. Cuanto más grande sea el valor de dicho coeficiente, mayor es la rigidez del neumático (v. Fig. 2) y, por consiguiente, mayor es el valor pico de la fuerza lateral. El valor de rigidez constante empleado para realizar los cálculos del modelo de Dugoff de las ecuaciones (15)-(17) y que permite la representación de las figuras 2 y 3 es de 48.400 N/º. Este es un valor representativo para simular el comportamiento del neumático ante condiciones típicas de carga y deslizamiento.

Puede verse en las ecuaciones (18) y (19) que la fuerza lateral es solo dependiente del ángulo de deslizamiento lateral y que la fuerza longitudinal lo es del deslizamiento longitudinal. Por lo que sustituyendo dichas ecuaciones en las ecuaciones (1)-(3), se puede obtener el modelo de bicicleta no lineal basado en Dugoff:

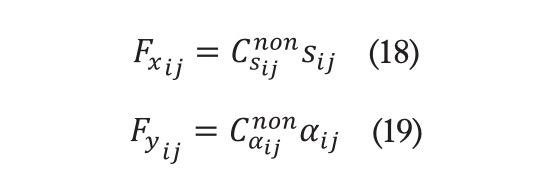
DISEÑO DEL CONTROLADOR PREDICTIVO BASADO EN MODELO

Algoritmo de control propuesto

El controlador predictivo basado en modelo (MPC) es una estrategia de control avanzado que utiliza un modelo matemático discreto del sistema para prever su comportamiento futuro y determinar las acciones de control óptimas. Este enfoque se basa en la definición de dos horizontes clave: el horizonte de predicción y el horizonte de control . El horizonte de predicción es el intervalo de tiempo en el que el controlador anticipa la dinámica futura del sistema, evaluando el impacto de las posibles acciones de control sobre las salidas del sistema. Por otro lado, el horizonte de control corresponde a la porción del horizonte de predicción en la que se optimizan y se aplican las acciones de control, usualmente limitado para simplificar el problema y para evitar elevados costes computacionales.

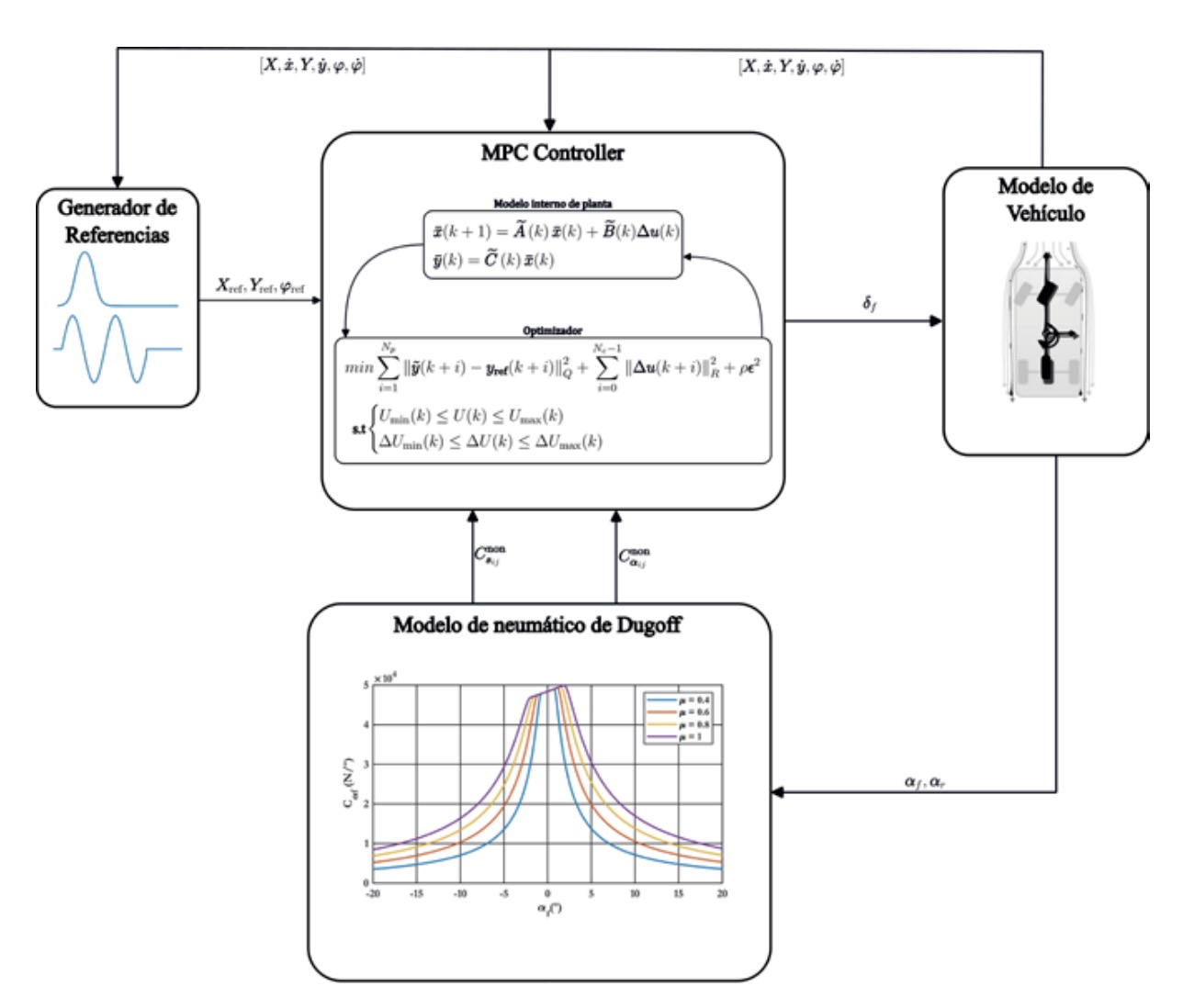
El principio fundamental del MPC consiste en resolver, en cada instante de tiempo, un problema de optimización que minimiza una función de coste, la cual combina los errores entre las salidas predichas y las referencias, así como los esfuerzos de control. Este cálculo se realiza bajo las restricciones físicas y operativas del sistema, como límites en los estados, salidas y entradas. Solo se aplica la primera acción de control de esta secuencia, y el proceso se repite en el siguiente paso, actualizando el modelo con las mediciones más recientes. La estructura del controlador puede verse en la figura 4.

El primer elemento importante es el generador de referencias, el cual, en función de la posición y velocidad estimada del vehículo, obtendrá para cada instante de tiempo , el conjunto de puntos que sirven como referencia durante todo el horizonte de predicción definido en el controlador. Otro elemento importante para destacar es el modelo de neumático de Dugoff. Tomando los ángulos de deslizamiento y como entrada, calcula internamente los coeficientes de rigidez no lineal y . El controlador, tomando los nuevos coeficientes de rigidez, actualiza el modelo interno del vehículo y predice el comportamiento de este a lo largo del horizonte de predicción. Finalmente, una vez predicho el comportamiento, se compara con el conjunto de puntos de la referencia y se obtiene la acción de control óptima. Esta última es el ángulo de dirección del vehículo.

 

Modelo empleado para la predicción

La discretización es un proceso esencial para el desarrollo de algoritmos de control de tipo predictivo, ya que estos emplean un modelo discreto del sistema dinámico interno para realizar la predicción sobre el comportamiento futuro de este. Es necesario representar en espacio de estados las ecuaciones (20)-(25). Para ello, seleccionamos como variables de estado la posición longitudinal x, la velocidad longitudinal , la posición lateral y, la velocidad lateral , el ángulo de rotación de vehículo (ángulo de guiñada) , la variación del ángulo , la desviación lateral Y y la desviación longitudinal X. El conjunto de variables de estado se agrupa de forma matricial, definiendo lo que se conoce como vector de estados x= . En las ecuaciones (20)-(23) se observa que el sistema también depende de la variable del ángulo de dirección . En sistemas de control aplicado al seguimiento de trayectorias, es muy habitual elegir como variable de control .

La forma general de representar la ecuación de estado es la siguiente:

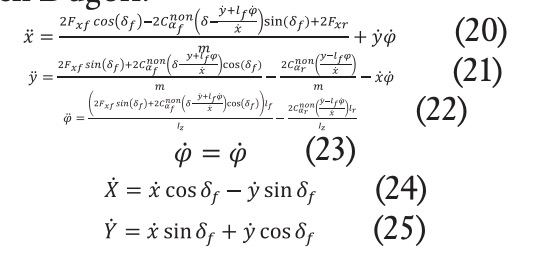
La variable de estado y la variable de control del vehículo de referencia satisface, para cualquier instante de tiempo, la ecuación de arriba. El subíndice r representa la variable de referencia:

El paso previo a la discretización es la linealización del sistema definido en la ecuación (26). Para ello, se realiza una expansión en series de Taylor alrededor de cualquier punto de referencia de la trayectoria, ignorando los términos de alto orden (Gao et al., 2024.):

Si se restan las ecuaciones (28) y (27) se obtiene:

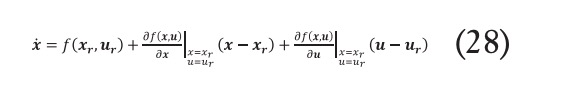
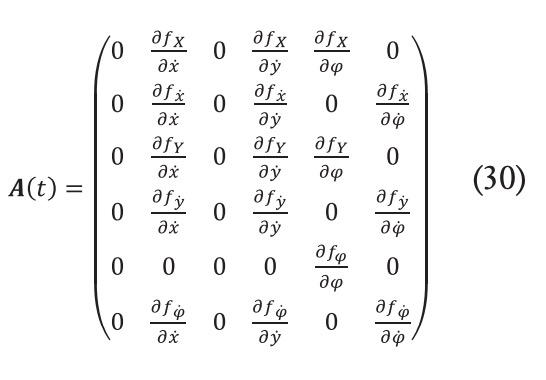
Donde las matrices y se conocen como matrices jacobianas, y representa las derivadas parciales de una función respecto de sus variables independientes. Estas variables de estado se agrupan dentro del vector de estados y la variable de control . Analíticamente, estas matrices se calculan:

Los términos de la matriz y son:

La fórmula (29) representa una ecuación de espacio de estados continua en el tiempo. Para su implementación en el algoritmo de control, esta debe discretizarse, ya que el MPC requiere de un modelo en espacio de estados discreto para poder realizar la predicción. Hay multitud de métodos de discretización de ecuación, cada uno con sus ventajas y desventajas en cuanto a los requisitos computacionales, precisión del seguimiento de la trayectoria, etc. (Gao et al., 2024.). En el presente artículo, se propone el método de discretización de Euler, que permite representar las matrices del sistema continuas y en su forma discreta:

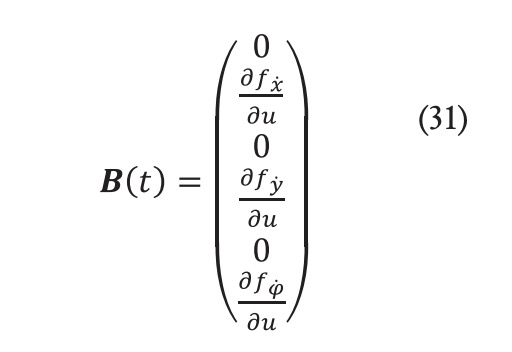es el tiempo de muestreo e , la matriz identidad cuya dimensión debe ser coincidir con la de la matriz . En este caso es una matriz 6×6. Una vez realizada la discretización, el nuevo modelo en espacio de estados que se obtiene es:

Ya que la variable de control es el ángulo de dirección de la rueda delantera , para poder asegurar un funcionamiento normal del vehículo y prevenir cambios repentinos en dicho ángulo, es crucial limitar el incremento del ángulo de dirección. Con este propósito, la ecuación (34) se transforma a su representación en forma de incrementos de la acción de control (Gao et al., 2024.). Esta reformulación permite que el sistema controle directamente los cambios en el ángulo, lo que es esencial para mantener una conducción suave y predecible, especialmente en escenarios en los que el comportamiento dinámico del vehículo puede verse afectado por variaciones rápidas:

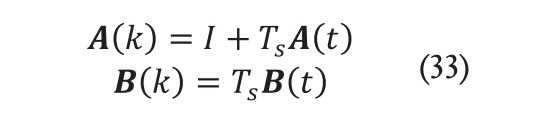
En la fórmula:

En el algoritmo propuesto, la referencia del controlador es el conjunto de puntos de la trayectoria objetivo, los cuales están definidos en el plano mediante su posición en , en y el ángulo de rotación respecto al punto anterior . Con el propósito de realizar el seguimiento del camino objetivo, las salidas del controlador serán aquellas que permiten ubicar el vehículo en el plano, y son: la posición longitudinal del vehículo en coordenadas globales X, la posición lateral en coordenadas globales Y y la rotación del vehículo o ángulo de guiñada . De esta manera, el MPC calculará la acción de control óptima que minimice el error existente entre la posición actual del vehículo y la trayectoria. En otras palabras, el objetivo es reducir la distancia entre el vehículo y la trayectoria conforme avanza la simulación [16]. Según los fundamentos de la representación de sistemas en espacio de estados, las salidas pueden obtenerse mediante la siguiente operación matricial:

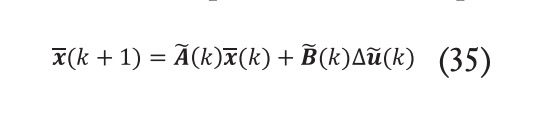Por lo que combinando las ecuaciones (35) y (36), se obtiene el modelo completo en espacio de estados discreto:

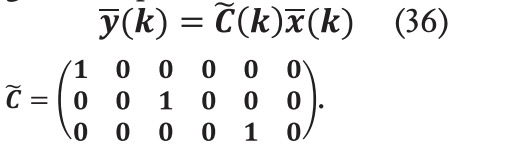
Cálculo de la salida en el dominio temporal de la predicción

Se asume que el horizonte de predicción es mayor que el horizonte de control . Basándose en la ecuación (37), se estima que se aplicarán incrementos de control durante el horizonte de control del sistema. Cuando el tiempo se encuentra en el horizonte de control, al pasar del horizonte de control al horizonte de predicción, la cantidad de control aplicada al sistema permanece constante y el incremento de la acción de control es 0. Tras realizar la derivación, se puede obtener la expresión de salida predicha del sistema (Gao et al., 2024.):

Definición de la función de coste objetivo

Como se comenta anteriormente, el MPC necesita de una función de coste que optimizar para calcular el valor óptimo de la acción de control. De esta manera, para garantizar que el vehículo autónomo sea capaz de seguir una trayectoria de referencia con precisión y de forma estable, es necesario optimizar el error existente entre la referencia y la posición del vehículo estimada y la acción de control. Se lleva a cabo la optimización del error a lo largo del horizonte de predicción y la de la acción de control a lo largo del horizonte de control . Además, es necesario restringir el incremento en la acción de control en cada periodo de muestreo, evitando variaciones bruscas y oscilaciones. Por consiguiente, refiriéndose al método de restricciones suaves utilizado en la literatura [18], la forma seleccionada de la función objetivo es la siguiente:

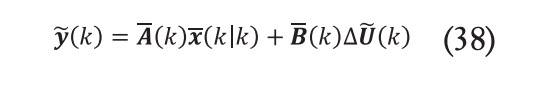En la fórmula, es el coeficiente de ponderación del factor de relajación de las restricciones . y son las matrices de pesos de la salida y de la variable de control, respectivamente. El primer término de la ecuación representa la acumulación del error existente entre la salida del sistema y la referencia de dicha salida. Es decir, captura la desviación entre ambas variables reflejando la capacidad de seguimiento de la trayectoria objetivo. El segundo término hace referencia a la acumulación de desviaciones de la variable de control. Refleja el requisito de cambio uniforme en dicha variable.

El tercer término garantiza que haya una solución óptima factible al realizar cambios en tiempo real. es el valor predicho de la salida para el tiempo discreto en el tiempo futuro es el valor de referencia de la salida para el tiempo discreto en el tiempo futuro es la secuencia del futuro de la variable de control.

Las matrices de pesos y se calculan del siguiente modo:

Realizando las operaciones necesarias para transformar el problema de optimización genérico definido por la función de coste de la ecuación (39) en su representación matricial[18], se obtiene la formulación típica de un problema de optimización cuadrática QP:

La matriz es la matriz hessiana, es el vector del gradiente lineal, es el vector de variables de decisión y es el vector de términos independientes. El cálculo de estas matrices puede verse a continuación:

Restricciones del problema de optimización

En algoritmos de control de tipo predictivo, es necesario imponer ciertas restricciones que deben cumplirse durante la resolución del problema de optimización definido por la ecuación (40). Generalmente, se definen restricciones en la propia variable de control y en su incremento y en las salidas. En escenarios reales de conducción, el ángulo de dirección tiene un rango limitado de giro, por lo que se debe tener en cuenta dicha limitación a la hora de diseñar el controlador. Al mismo tiempo, para tener en cuenta la estabilidad del vehículo al realizar el seguimiento de la trayectoria, también se debe limitar el incremento de la variable de control. Además, para evitar desviaciones excesivas del camino de referencia, se debe limitar también el valor máximo y mínimo de la posición longitudinal, lateral y del ángulo de guiñada.

Dicho lo cual, las restricciones impuestas al valor máximo y mínimo de la acción de control:

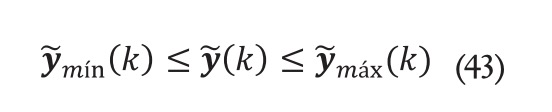
es el valor mínimo de la variable de control y es el valor máximo. Se imponen también restricciones al incremento de la variable de control:

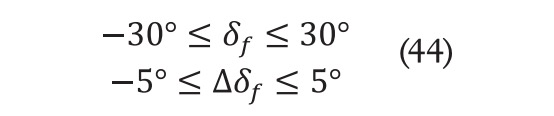(42) es el valor mínimo del incremento de control y es el valor máximo del incremento. E imponiendo restricciones a las salidas:

 

SIMULACIÓN

Para validar el rendimiento del controlador MPC no lineal propuesto, se realizan diversos escenarios de simulación en el entorno de Matlab/Simulink. Estos escenarios incluyen maniobras típicas como el doble cambio de carril y el camino sinusoidal. Además, las pruebas se llevan a cabo tanto a velocidad constante como a velocidad variable, lo que permite analizar el efecto de la aceleración longitudinal en el control. Por último, se plantea un escenario que considera un trazado complejo, compuesto por segmentos rectos y curvos, ejecutado a velocidad constante.

Parámetros de la simulación

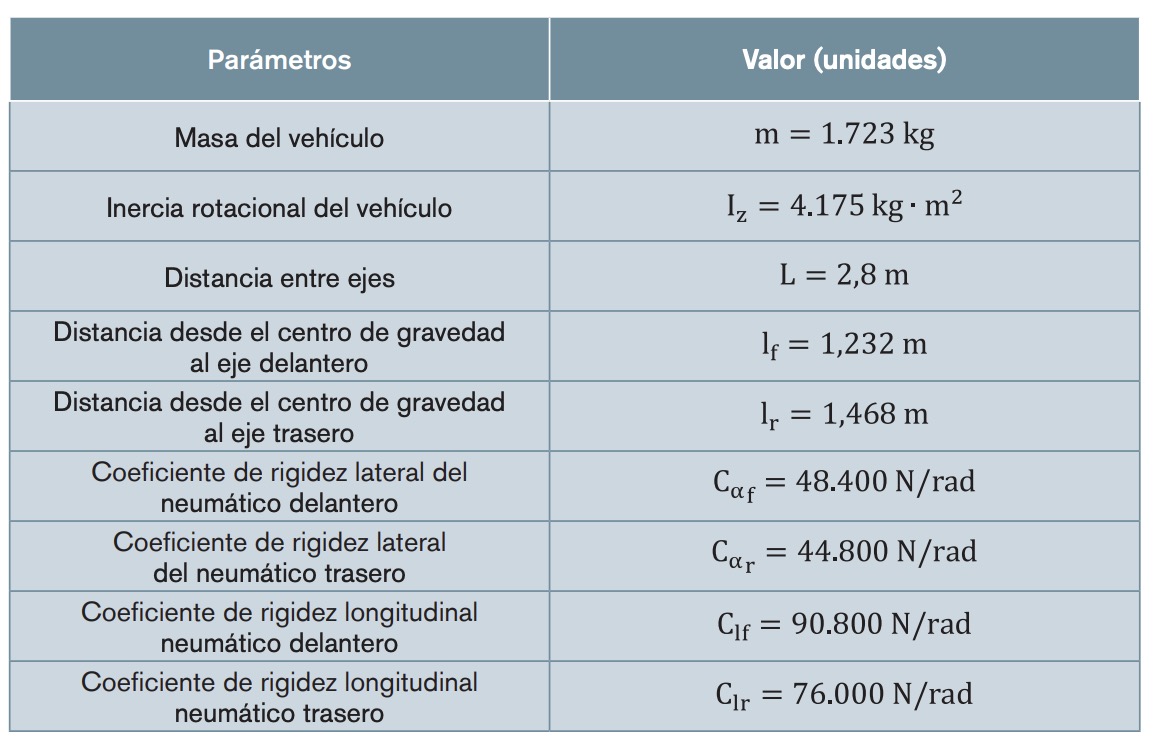
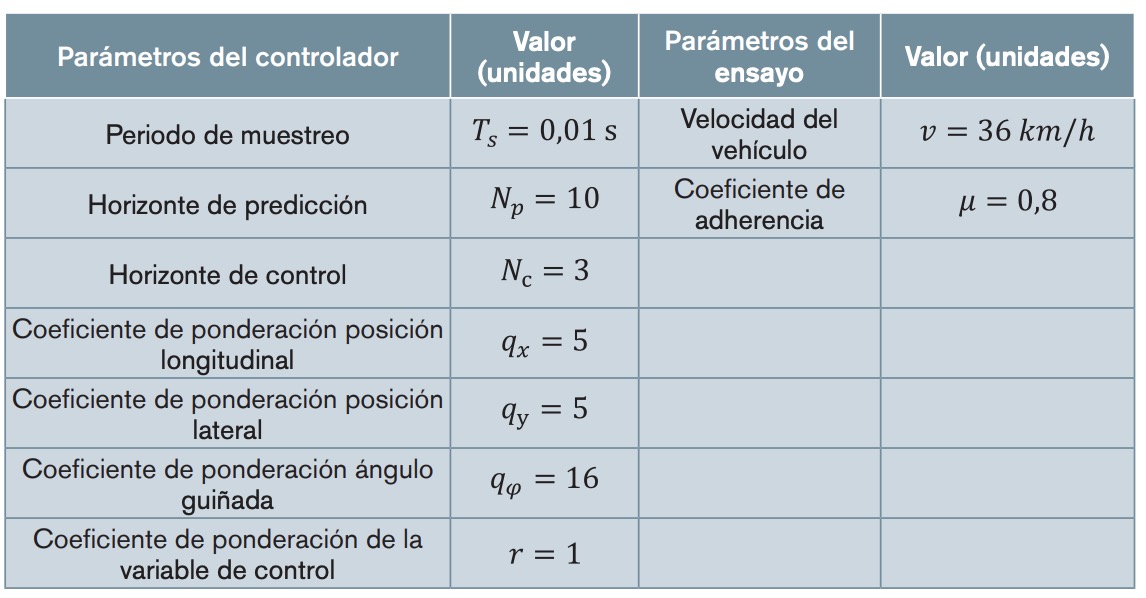
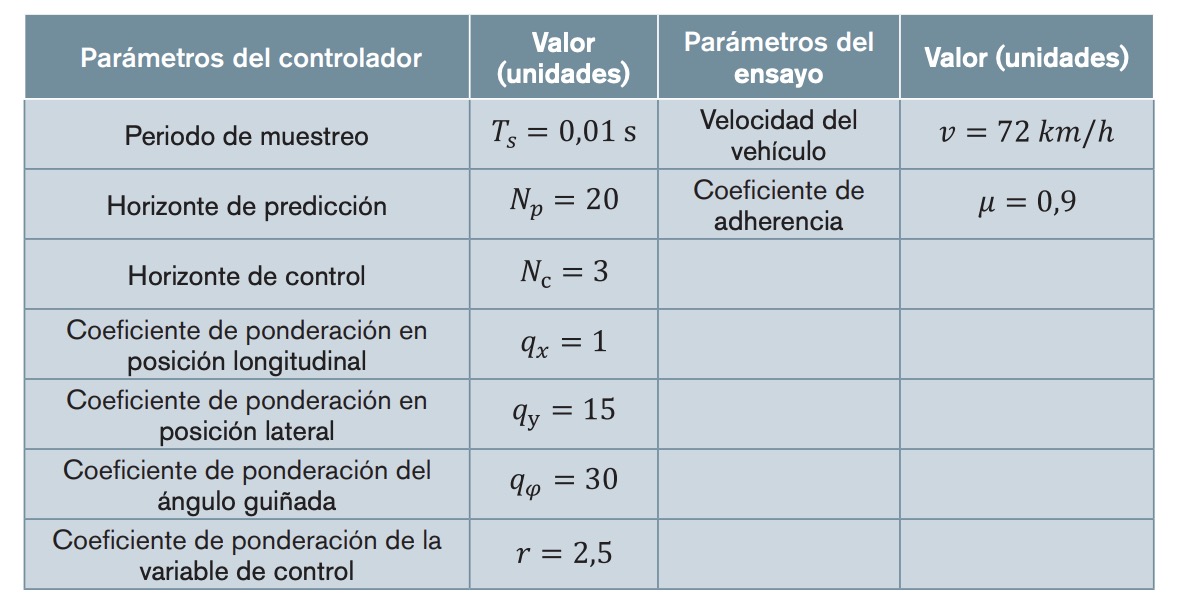
Los parámetros mecánicos del vehículo empleado para realizar las diferentes simulaciones se recogen en la tabla 1. En línea con [18], las restricciones que se imponen a la variable de control y a la variación de esta son:

Escenario 1: simulación a velocidad constante baja y coeficiente de adherencia elevado

Se propone estudiar la precisión del controlador ante un escenario de velocidad del vehículo constante y la maniobra de referencia es el doble cambio de carril. Esta maniobra se usa ampliamente en ensayos en los que se mide la estabilidad y la maniobrabilidad del vehículo.

El controlador propuesto se basa en el modelo no lineal de neumático de Dugoff, el cual, partiendo de un coeficiente rigidez de referencia, para el neumático delantero y para el neumático trasero, obtiene un nuevo coeficiente de rigidez no lineal que tiene en cuenta rangos de trabajo del neumático en los que se pierde la proporcionalidad entre la fuerza y el ángulo de deslizamiento. Para reflejar el rendimiento de este primer controlador no lineal NMPC, se compara con un controlador MPC convencional. Este no considera la región no lineal del neumático y está diseñado bajo la simplificación de coeficiente de rigidez lateral y longitudinal constante. En la tabla 2 se recogen los parámetros del controlador para este escenario de simulación:

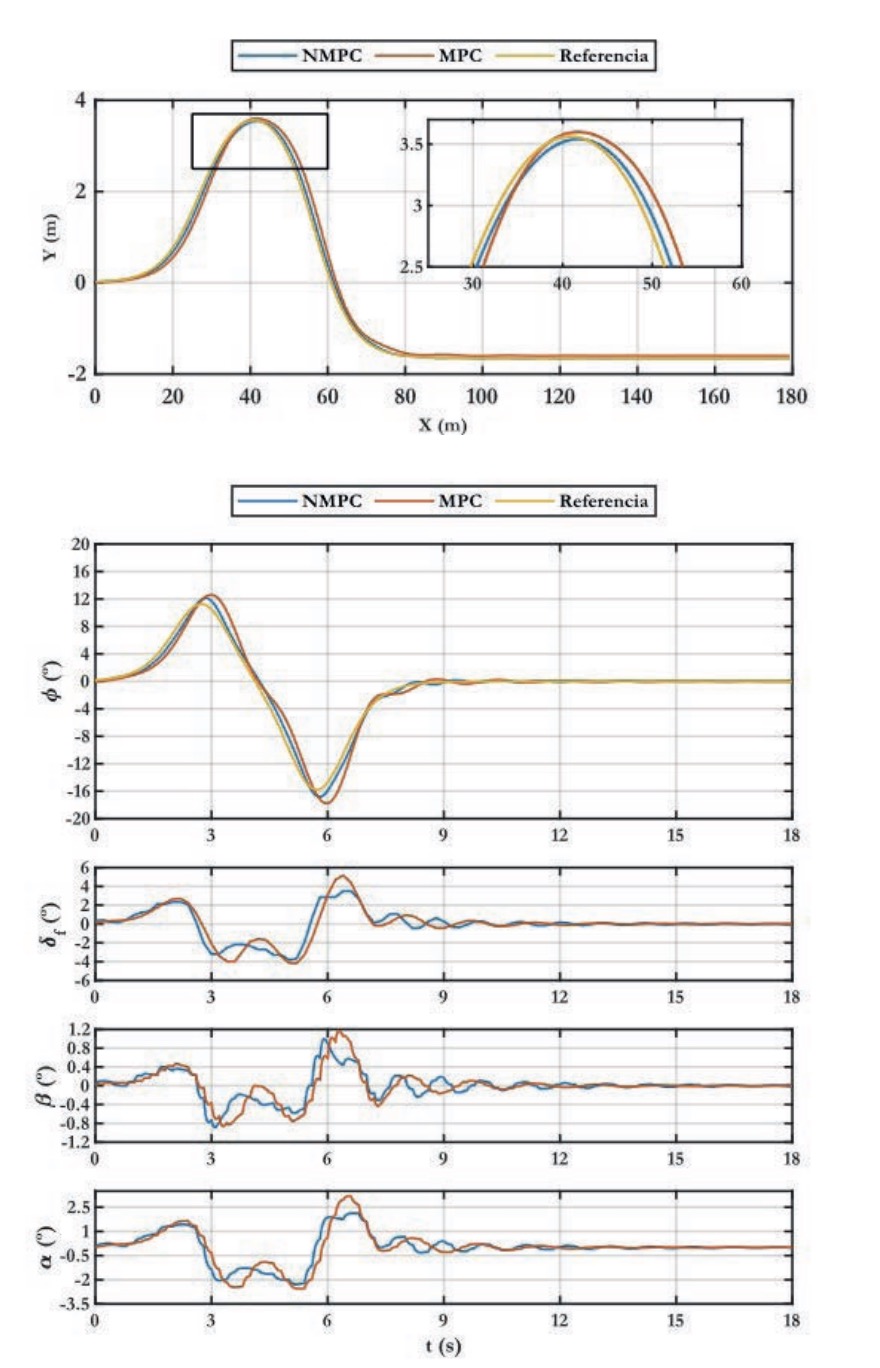
En la figura 5 puede observarse la efectividad que tienen ambos controladores para seguir la referencia de posición lateral. Bajo unas condiciones de adherencia elevada =0,9 y velocidad baja = 36 km/h, ambos controladores muestran una gran exactitud a la hora de seguir la trayectoria. Pero, al fijarse en el detalle de la zona remarcada, puede verse que el controlador NMPC muestra mayor precisión y consigue que la trayectoria que describe el vehículo controlado esté más próxima a la de la referencia. Esta diferencia de rendimiento entre ambos controladores se acentúa en las zonas en las que la curvatura es mayor, hasta alcanzar ángulos de deslizamiento más elevados y acercándose a la zona de trabajo no lineal del neumático. Aunque en dichas condiciones de trabajo se puede suponer que las fuerzas sobre los neumáticos son constantes, el controlador NMPC puede describir con mayor rigor las fuerzas sobre los neumáticos que el controlador lineal MPC. Muestra, por consiguiente, mayor capacidad de seguimiento de la referencia.

En la figura 5a, se representa el ángulo de guiñada de referencia que debe seguir el vehículo para poder seguir la trayectoria con la mayor precisión y estabilidad. Se observa que el ángulo que describe el vehículo controlado por el NMPC está más próximo al ángulo objetivo en prácticamente todo el trazado. Resalta esta discrepancia en las zonas en las que la curvatura es mayor y se alcanzan mayores ángulos de deslizamiento. En la figura 5b-d se describen el ángulo de la dirección, el de deslizamiento del vehículo y el de deslizamiento del neumático delantero del controlador NMPC y del controlador MPC, que son parecidos, ya que la magnitud y la forma que describen es parecida. Aunque justamente las pequeñas fluctuaciones existentes entre ambos controladores se dan en el rango de 6-8 segundos, cuando se ejecuta la última curva de la maniobra. Una vez superada dicha zona, se observa que las oscilaciones se van atenuando con el tiempo, y son mayores las del MPC, lo que también demuestra una peor capacidad de corregir el error en el régimen permanente. En definitiva, el rendimiento de ambos controladores es muy parecido, ya que ambos pueden seguir la trayectoria con precisión y fluidez, aunque queda demostrado que en zonas en las que se alcanzan mayores aceleraciones laterales y mayores ángulos de deslizamiento, el controlador NMPC se ajusta mejor, debido a su capacidad de modelizar con mayor precisión el comportamiento del neumático.

 

Escenario 2: simulación a velocidad constante elevada y coeficiente de adherencia alto

En el escenario 1 se ha demostrado que, ante unas condiciones de favorables, ambos controladores exhiben una elevada precisión a la hora de realizar el seguimiento del camino de referencia. Es ligeramente superior el NMPC. En el presente escenario, se eleva la velocidad a =20 m/s y se mantiene el coeficiente de adherencia a =0,9. La maniobra que se ejecuta sigue siendo el cambio de carril. Los controladores que se comparan siguen siendo los mismos, un NMPC basado en el modelo de Dugoff de neumático y un MPC clásico lineal. Se debe implementar unos cambios en los parámetros del controlador. En la tabla 3 se recogen los parámetros de los controladores y del ensayo:

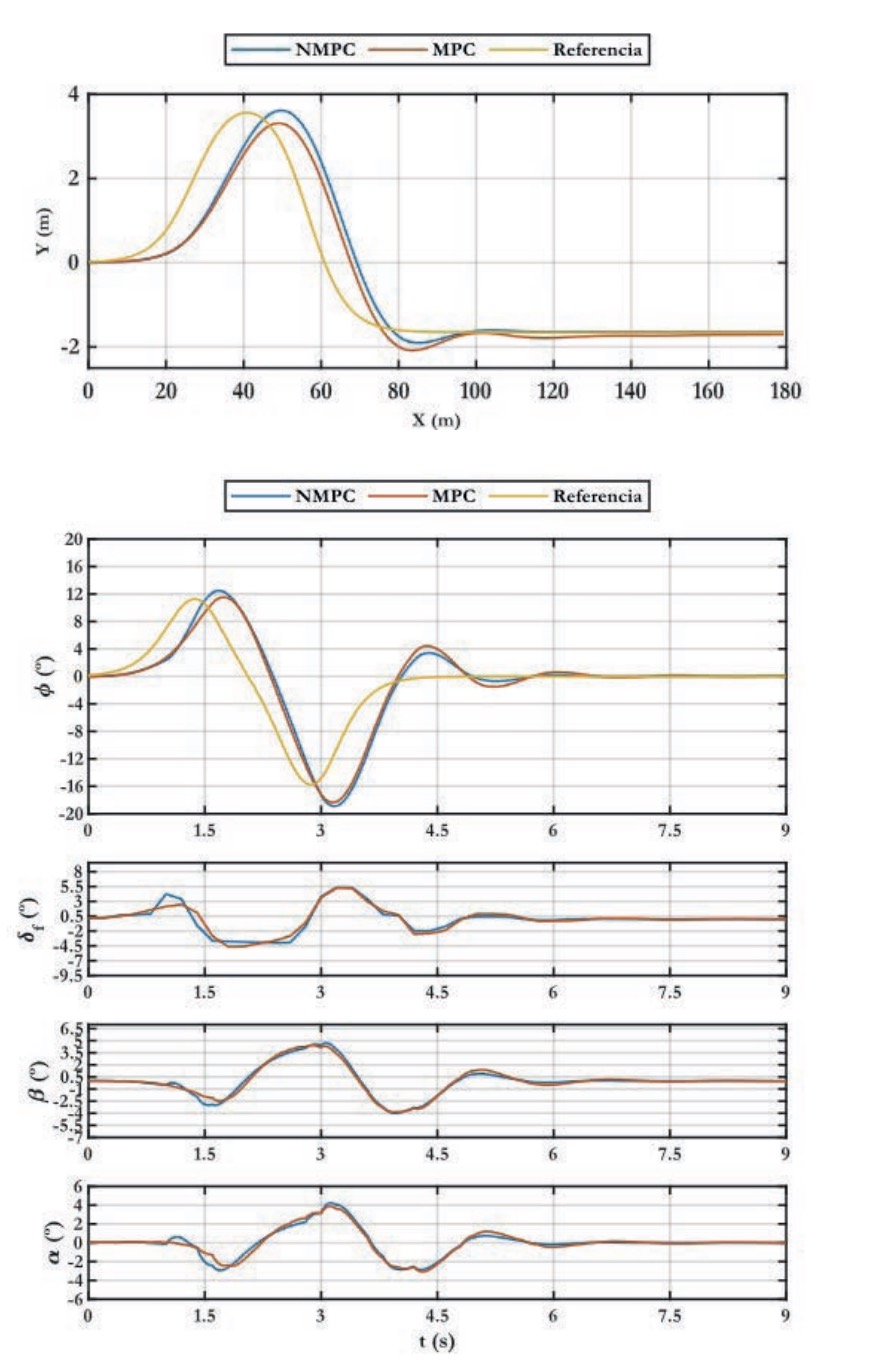
Al haberse incrementado la velocidad longitudinal al doble que en el escenario 1, la capacidad global de seguir la referencia de ambos controladores disminuye. En la figura 6 se observa que ninguno de los controladores puede seguir la referencia lateral con suficiente exactitud, y es el NMPC el que muestra mayor precisión. Esto puede verse en el tramo entre 25 y 60 metros, en el que la trayectoria del controlador NMPC se encuentra más próxima a la maniobra objetivo que el MPC. También el controlador no lineal puede corregir el error en régimen permanente. Se observa en el tramo de los 100 metros hasta el final del recorrido, donde el NMPC corrige perfectamente la trayectoria y el MPC no puede hacerlo completamente.

Por otro lado, en la figura 6a se puede visualizar la capacidad de seguimiento de la referencia del ángulo de guiñada de los controladores. En este caso, las discrepancias entre ambos son menores, y es el controlador no lineal NMPC el que se queda más próximo. Pero, a diferencia de lo ocurrido en el seguimiento de la referencia lateral, los dos controladores sí pueden corregir el error del régimen permanente. Esto puede verse a partir de los 4,5 segundos de simulación, cuando se amortiguan las oscilaciones y se demuestra que el sistema tiene una respuesta estable. En la figura 6b-d, se observa la evolución de los ángulos de dirección, deslizamiento de vehículos y del neumático, respectivamente. Ambos describen curvas muy similares. La mayor diferencia entre dichas curvas se observa en el primer segundo de la simulación, coincidiendo con el inicio de la maniobra del cambio de carril y cuando la aceleración lateral del vehículo se ve incrementada. Este efecto se traduce en un aumento del ángulo de deslizamiento lateral del neumático, y se alcanzan valores que se quedan fuera de la zona lineal de trabajo de este, lo que justifica el mejor rendimiento del controlador NMPC frente al MPC.

 

CONCLUSIONES

En este artículo se diseña un algoritmo de control predictivo basado en el modelo no lineal del neumático. Este permite reducir el error de cálculo de las fuerzas de los neumáticos del vehículo ante condiciones adversas, como zonas con muy baja adherencia, elevadas velocidades, etc.., y se evita el deterioro en la capacidad de seguimiento de maniobras bajo dichas condiciones. En el controlador no lineal propuesto, las fuerzas se caracterizan mediante funciones no lineales basadas en el modelo de Dugoff, en vez de hacer uso de la aproximación del comportamiento lineal del neumático, el cual, según se comenta previamente, presenta ciertas limitaciones en su aplicación. Durante el proceso de diseño del controlador, se hace uso de la expansión en series de Taylor ampliamente usada en el proceso de linealización de sistemas complejos. Esto es determinante para la construcción de las matrices características que permiten la resolución del problema de optimización. Posteriormente, se lleva a cabo un proceso de discretización del sistema mediante el método de Euler. Para poder validar el potencial del controlador propuesto, se llevan a cabo una serie de simulaciones bajo distintas condiciones y se compara con el controlador lineal clásico MPC. El primer escenario consiste en realizar la maniobra de cambio de carril a una velocidad baja y un coeficiente de adherencia alto. Ambos controladores muestran una gran precisión a la hora de realizar el seguimiento de la trayectoria, y el controlador no lineal es ligeramente superior. En el segundo escenario se duplica la velocidad y se mantiene la trayectoria y la adherencia. Aquí ambos controladores pierden rendimiento; muestra mayor estabilidad y precisión el controlador no lineal NMPC. Como trabajo futuro, se propone ampliar la cantidad de ensayos que realizar, variando las condiciones de trabajo. Esto incluye escenarios que simulen conducción en superficies con bajo coeficiente de adherencia, velocidad variable, etc., además de probar otras maniobras típicas de ensayos como el camino senoidal o de serpiente o un camino aleatorio que incluya trazados con diferentes curvaturas.

 

BIBLIOGRAFÍA

Chen L, Bian M, Luo Y, Li K. (2013). Maximum tire road friction estimation based on modified Dugoff tire model. In Proceedings of the 2013 International Conference on Mechanical and Automation Engineering (p. 56-61). IEEE. https://doi. org/10.1109/MAEE.2013.24

Cheng S, Li L, Chen X, Wu J, Wang HD. (2021). Model-predictive-control-based path tracking controller of autonomous vehicle considering parametric uncertainties and velocity-varying. IEEE Transactions on Industrial Electronics, 68(9), p. 8698-707. https://doi.org/10.1109/ TIE.2020.3009585.

Falcone P, Borrelli F, Asgari J, Tseng HE, Hrovat D. (2007). Predictive active steering control for autonomous vehicle systems. IEEE Transactions on Control Systems Technology, 15(3), 566-80. https://doi. org/10.1109/TCST.2007.894653.

Falcone P, Tseng HE, Borrelli F, Asgari J, Hrovat D. (2008). MPC-based yaw and lateral stabilisation via active front steering and braking. Vehicle System Dynamics, 46(6), 611-28. https://doi. org/10.1080/00423110802018297.

Frendi S, Mellah R, Seddiki L, Akdag H. (2016). Tracking controller design of a sideslip angle and yaw rate for electrical vehicle bicycle model. IFAC-PapersOnLine, 49(11), 169- 74. https://doi.org/10.1016/j.ifacol.2016.07.108.

Gao Y, Wang X, Huang J, Yuan L. (2024). Adaptive model predictive control for intelligent vehicle trajectory tracking considering road curvature. International Journal of Automotive Technology, 25(5), 1051-64. https://doi.org/10.1007/ s12239-024-00086-8.

Häne C, Sattler T, Pollefeys M (s.f.). Obstacle detection for self-driving cars using only monocular cameras and wheel odometry.

Huang G, Ma Q. (2022). Research on path planning algorithm of autonomous vehicles based on improved RRT algorithm. International Journal of Intelligent Transportation Systems Research, 20(1), 170-80. https://doi.org/10.1007/s13177-021- 00281-2.

Lee K, Jeon S, Kim H, Kum D. (2019). Optimal path tracking control of autonomous vehicle: Adaptive full-state linear quadratic Gaussian (LQG) control. IEEE Access, 7, 109120-33. https://doi.org/10.1109/ ACCESS.2019.2933895.

Li Q, Zheng N, Cheng H. (2004). Springrobot: A prototype autonomous vehicle and its algorithms for lane detection. IEEE Transactions on Intelligent Transportation Systems, 5(4), 300-8. https://doi.org/10.1109/ TITS.2004.838220.

Lin F, Sun M, Wu J, Qian C. (2021). Path tracking control of autonomous vehicle based on nonlinear tire model. Actuators, 10(9), 241. https://doi. org/10.3390/act10090242.

Naranjo JE, González C, García R, De Pedro T. (2008). Lane-change fuzzy control in autonomous vehicles for the overtaking maneuver. IEEE Transactions on Intelligent Transportation Systems, 9(3), 438-50. https://doi.org/10.1109/ TITS.2008.922880.

Taghavifar H, Rakheja S. (2019). Path-tracking of autonomous vehicles using a novel adaptive robust exponential-like-sliding-mode fuzzy type-2 neural network controller. Mechanical Systems and Signal Processing, 130, 41-55. https://doi. org/10.1016/j.ymssp.2019.04.060.

Tchamna R, Youn I. (2013). Yaw rate and side-slip control considering vehicle longitudinal dynamics. International Journal of Automotive Technology, 14(1), 53-60. https:// doi.org/10.1007/s12239-013-0007- 1.

Urmson C. Self-Driving Cars in the Urban Challenge.

Yu S, Hirche M, Huang Y, Chen H, Allgöwer F. (2021). Model predictive control for autonomous ground vehicles: A review. Autonomous Intelligent Systems, 1(1), 1-24. https://doi.org/10.1007/s43684-021- 00005-z.

Yuan CC, Wei Y, Wang T, et al. (2020). Research on path planning based on new fusion algorithm for autonomous vehicle. Advances in Mechanical Engineering. https://doi. org/10.1177/1729881420911235.

Zaarane A, Slimani I, Al Okaishi W, Atouf I, Hamdoun A. (2020). Distance measurement system for autonomous vehicles using stereo camera. Array, 5, 100016. https://doi. org/10.1016/j.array.2020.100016.