Estudio del comportamiento vibratorio de vigas dañadas de material compuesto mediante redes neuronales artificiales

Patricia Rubio Herrero1, Belén Muñoz-Abella1, Inés Iváñez del Pozo2, Lourdes Rubio Ruiz de Aguirre1

 

Resumen

Las vigas rotatorias son simplificaciones de componentes mecánicos más complejos, característicos de áreas estratégicas, como palas de aerogeneradores. Si la viga presenta un defecto, este modifica su comportamiento dinámico y los valores de las frecuencias naturales. En este estudio, se presenta una metodología basada en redes neuronales artificiales (RNA) que permite calcular el valor de las cuatro primeras frecuencias naturales de vigas dañadas de material compuesto que combinan pieles de polímeros reforzados con fibra de carbono y núcleo de nido de abeja en función de la velocidad de rotación y de las características del defecto (tamaño y localización). Los datos requeridos para entrenar la RNA se han obtenido a partir de un modelo numérico dinámico tridimensional de una viga sándwich que presenta una discontinuidad transversal en el núcleo. Las frecuencias naturales de la viga se han obtenido aplicando la transformada rápida de Fourier a las aceleraciones calculadas por el modelo. La RNA propuesta presenta una excelente alternativa para el análisis de la respuesta vibratoria de vigas sándwich dañadas, ya que es eficiente y fácil de usar, a la vez que tiene un bajo coste computacional.

Palabras clave: Vigas rotatorias dañadas, frecuencias naturales, material compuesto, defecto en el núcleo y redes neuronales artificiales.

 

Abstract

Rotating beams are simplifications of more complex mechanical components, characteristic of strategic areas, such as wind turbine blades. If the beam has a defect, this modifies its dynamic behaviour and natural frequency values. This study presents a methodology based on artificial neural networks (ANNs) that allows the calculation of the values of the first four natural frequencies of damaged composite beams formed by carbon fibre reinforced polymer ace-sheets and a honeycomb core as a function of the rotation speed and the characteristics of the defect (size and location). The data required to train the ANN has been obtained from a three-dimensional dynamic numerical model of a sandwich beam with a transverse discontinuity in the core. The natural frequencies of the beam have been obtained by applying the fast Fourier transform to the accelerations calculated by the model. The proposed ANN is an excellent alternative for analysing the vibrational response of damaged sandwich beams, as it is efficient and easy to use, while also having a low computational cost..

Keywords: Damaged rotating beams, natural frequencies, composite material, core defect, and artificial neural networks.

---

Recibido/received: 03/07/2025

Aceptado/accepted: 27/10/2025

1Dpto. de Ingeniería Mecánica. Universidad Carlos III de Madrid.

2Dpto. Mecánica de Medios Continuos y Teoría de Estructuras. Universidad Carlos III de Madrid.

Autor para correspondencia: Patricia Rubio Herrero; e-mail: pr****@******3m.es.

---

1. INTRODUCCIÓN

Las energías renovables se distinguen por su reducido impacto ambiental ya que, a diferencia de los combustibles fósiles, no afectan al cambio climático. Una de las fuentes de energía renovables con mayor potencial es la energía eólica, cuyo crecimiento está experimentando un notable impulso. Las palas son uno de los elementos constitutivos principales de los sistemas de energía eólica. Su integridad estructural puede verse amenazada por la presencia de defectos, que pueden dar lugar a roturas catastróficas y a elevados costes de mantenimiento. Por ello, es fundamental contar con técnicas de detección de defectos que faciliten la implementación de planes de mantenimiento adecuados, evitando así pérdidas derivadas del fallo total del sistema.

Normalmente, al abordar el estudio dinámico de este tipo de elementos, las palas con geometrías complicadas se modelan habitualmente de manera simplificada utilizando vigas rotatorias. En las últimas décadas, numerosos autores han estudiado la detección de defectos en componentes mecánicos (Chen, 1988; Kim, 2003; Ozdemir, 2014; Lee, 2017; Valverde-Marcos, 2022; Bhat, 1986). No obstante, son pocos los estudios dedicados a la estimación de defectos en palas rotatorias dañadas. La presencia del defecto modifica el comportamiento dinámico de la viga y, entre otros, modifica los valores de las frecuencias naturales, por lo que su variación es habitualmente utilizada para determinar la aparición de un defecto. En el caso de las vigas rotatorias, el comportamiento dinámico en el plano de giro (chordwise) y fuera de él (flapwise), depende de la fuerza centrífuga que aparece debida a la rotación, y que es variable con la distancia al centro de giro. La aparición de esta fuerza introduce un aumento de la frecuencia natural en ambos planos (Chen, 1988; Bhat, 1986). Por otra parte, si la viga giratoria contiene un defecto, se produce un aumento de la flexibilidad que se traduce en la disminución de las frecuencias naturales. La compensación de ambos efectos puede dificultar la detección del daño (Chen, 1988).

Asimismo, la mayoría de las investigaciones se han centrado en el estudio de palas hechas de materiales convencionales (Lee, 2017; Valverde-Marcos, 2022; Bhat, 1986). Sin embargo, las palas de aerogeneradores normalmente se fabrican con materiales compuestos y la detección de fallos en vigas rotatorias de material compuesto dañado es un campo menos explorado (Kim, 2003; Ozdemir, 2014). Se suelen utilizar estructuras sándwich, formadas por pieles de laminados de fibra de vidrio (GFRP) y núcleos de espuma polimérica (foam). No obstante, con el aumento del tamaño de los aerogeneradores, surge la necesidad de emplear materiales más ligeros, pero igualmente resistentes para las palas, con el fin de reducir su peso. Por esta razón, en este estudio se ha optado por estructuras sándwich que combinan núcleos de nido de abeja (honeycomb) y pieles de polímeros reforzados con fibra de carbono (CFRP). Para el núcleo, se propone el uso de núcleos de nido de abeja, que consisten en celdas unitarias unidas de forma similar a un panal de abejas, lo que minimiza la cantidad de material utilizado, reduciendo así el peso y proporcionando una excelente resistencia (Sezgin, 2008), y para las pieles, se proponen materiales compuestos de fibra de carbono (CFRP) que poseen un reducido peso y unas excelentes propiedades mecánicas (Marsh, 2005). En cuanto a la detección de defectos en vigas rotatorias fabricadas con este tipo de materiales, los autores no han encontrado estudios previos en la literatura disponible.

Las redes neuronales artificiales (RNA) son sistemas computacionales inspirados en la estructura y el funcionamiento del cerebro humano y el sistema nervioso biológico. Su propósito principal es aprender a partir de grandes cantidades de datos para reconocer patrones, clasificar información y predecir resultados, de una manera similar a como lo hace la inteligencia humana. Están compuestas por varias capas: una capa de entrada, capas intermedias denominadas ocultas y una capa de salida. A través de un proceso de entrenamiento aprenden a establecer la relación entre los datos de entrada y los de salida. Las RNA constituyen una herramienta ampliamente adoptada en el campo de la ingeniería por muchos investigadores y han demostrado ser útiles en la detección y en la identificación de defectos en componentes mecánicos (Sekhar, 2008; Youngho, 2012).

En este trabajo, se ha utilizado una RNA para determinar las frecuencias naturales de una viga rotatoria de material compuesto con pieles de polímeros reforzados con fibra de carbono y núcleo de nido de abeja que presenta una discontinuidad transversal en el núcleo. Para ello, se ha desarrollado un modelo 3D de elementos finitos en el código Abaqus/Implicit de una viga rotatoria de material compuesto y se han estudiado en detalle sus características vibratorias en función del tamaño, la localización de la discontinuidad y la velocidad de rotación. Se ha elegido la aceleración de un punto de la sección ubicado en el extremo de la viga como señal de salida del modelo numérico. La señal ha sido procesada para obtener las frecuencias de la viga rotatoria. A partir de los datos del modelo numérico, se ha derivado la RNA. La metodología propuesta ofrece una excelente opción para analizar las vibraciones de vigas rotatorias dañadas fabricadas con estructuras sándwich formadas por pieles de CFRP y un núcleo de nido de abeja y se podría utilizar como base para el futuro desarrollo de un algoritmo de detección e identificación de defectos.

 

2. MODELO DE LA VIGA ROTATORIA DAÑADA

2.1 Modelo geométrico

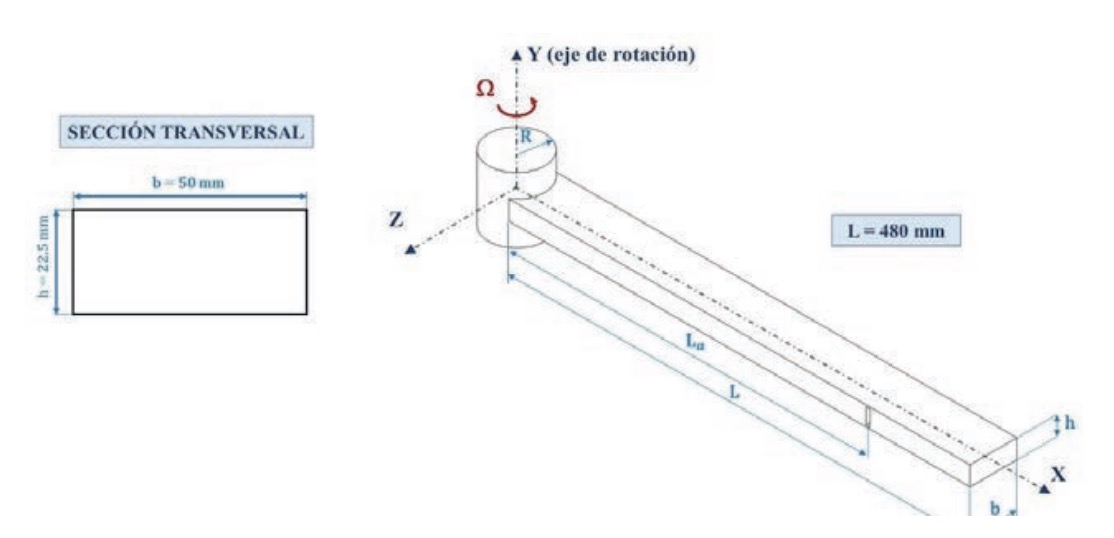
Se ha considerado una viga rotatoria fabricada de material compuesto que combina pieles de laminados de fibra de carbono (CFRP) y núcleo de nido de abeja (honeycomb) de Nomex®, cuyas dimensiones pueden verse se la figura 1. La viga gira con sentido antihorario alrededor del eje de revolución Y con velocidad angular constante ? y presenta una discontinuidad en el núcleo a una distancia La del extremo de la viga.

Se ha analizado el comportamiento vibratorio en función de las siguientes variables:

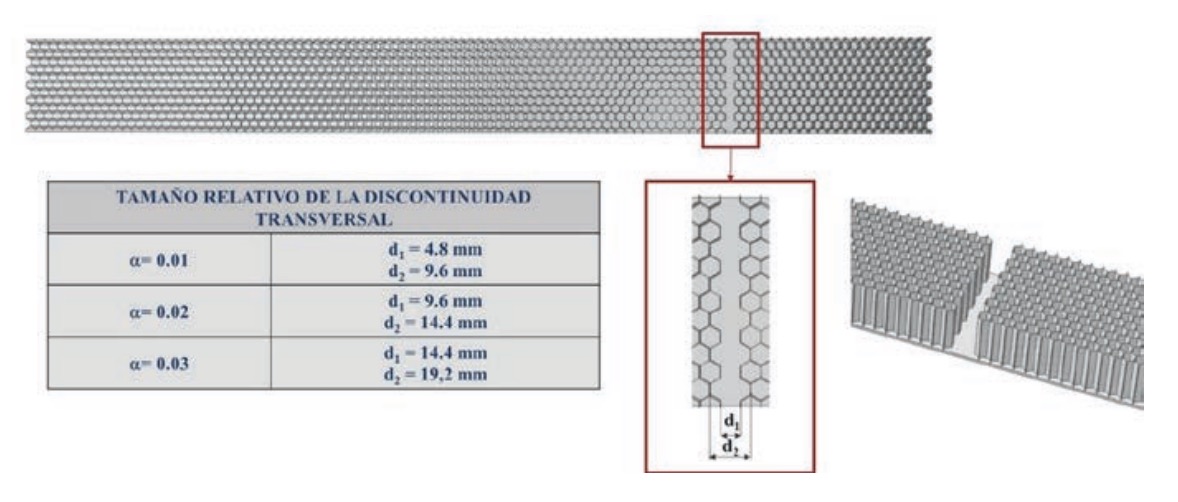
• El tamaño relativo de la discontinuidad = d1/L. Se han considerado diferentes tamaños relativos de la discontinuidad en el núcleo: = 0, 0,01, 0,02 y 0,03; el valor = 0 corresponde a una viga intacta. La figura 2 muestra la geometría de la discontinuidad transversal.

• La ubicación relativa de la discontinuidad = Lh/L. Se han considerado las siguientes ubicaciones: = 0,14, 0,355, 0,57 y 0,785.

• La velocidad de giro ?. Se han considerado 8 velocidades de giro de la viga (? = 30, 40, 50, 60, 70, 80, 90 y 100 rad/s).

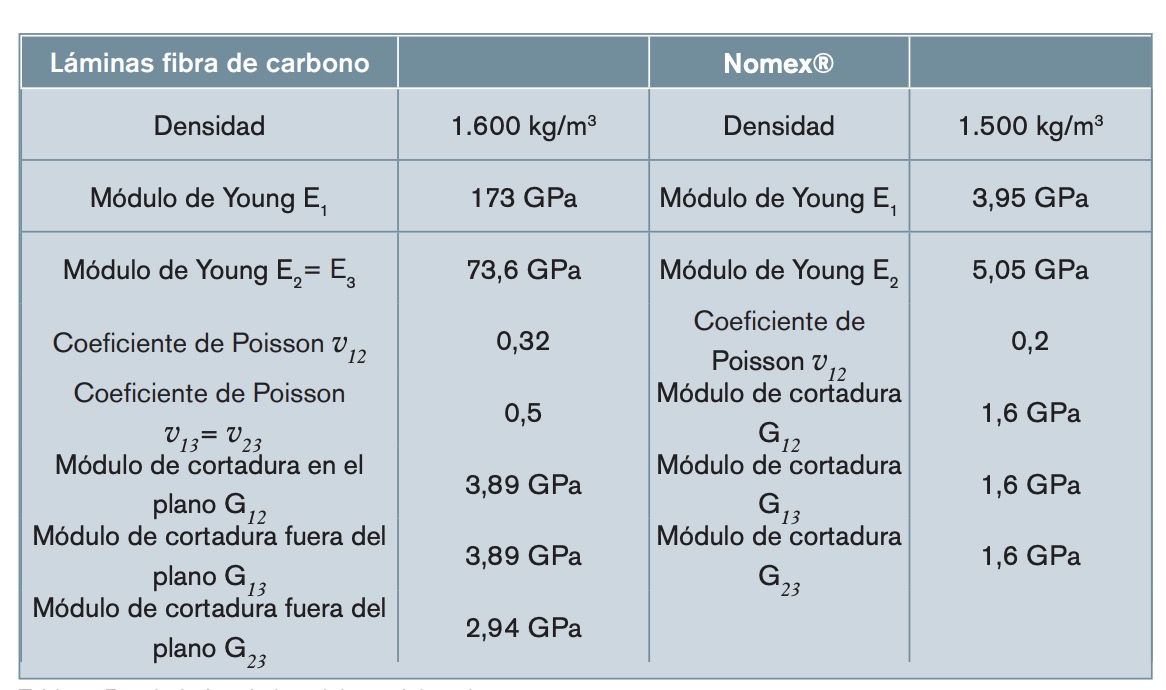
La viga sándwich está formada por dos pieles exteriores de CFRP y núcleo de nido de abeja de Nomex®. Las pieles constan de un laminado de 16 láminas de fibra de carbono en matriz epoxi, IM7/MTM-45-1 con una secuencia de apilamiento igual a [0/+45/90/-45]2S (Ridgard, 2008). El núcleo de nido de abeja está fabricado en Nomex® con denominación ANA-3.2, y está formado por celdas hexagonales y huecas, con una densidad nominal de 48 kg/mm3 (Honeycom, 2023). En la tabla 1 se muestran las propiedades de las pieles y del núcleo. Las direcciones 1, 2 y 3 coinciden con las direcciones X, Y y Z, respectivamente.

 

2.2 Modelo numérico

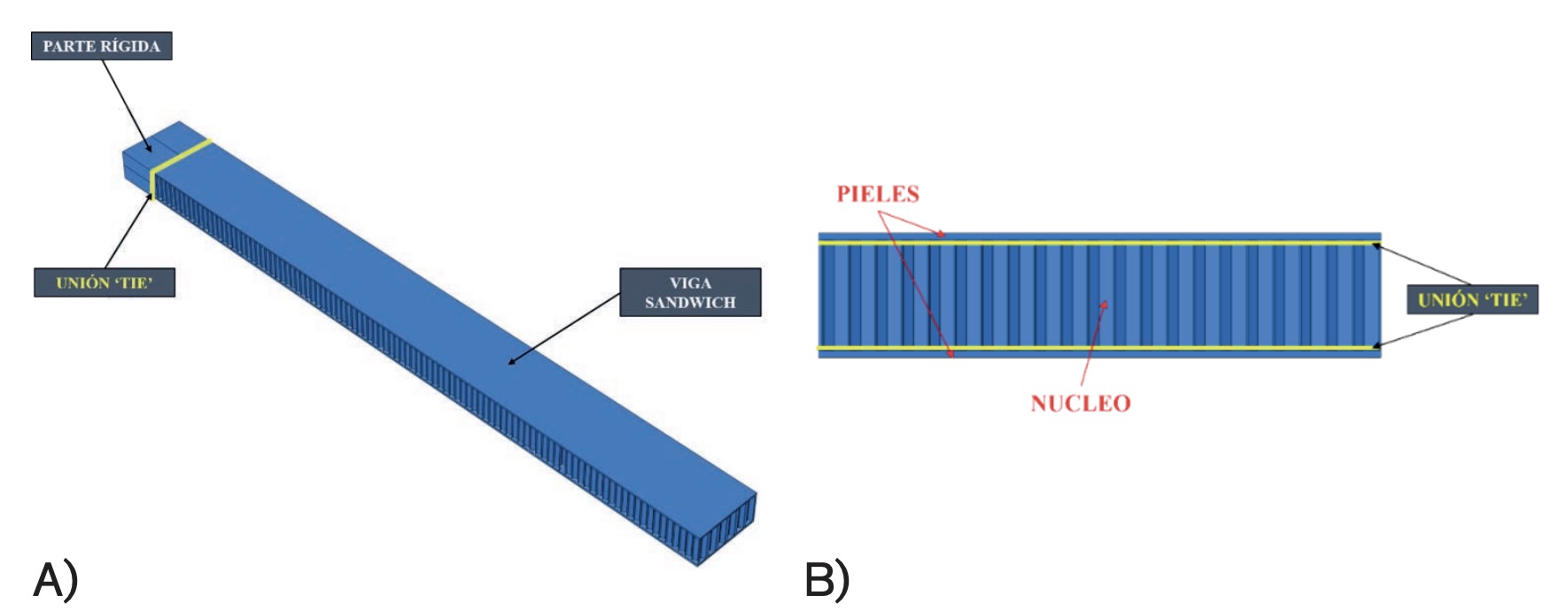
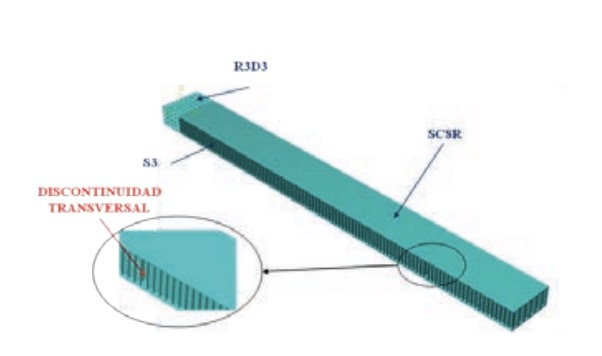
El estudio numérico se ha llevado a cabo mediante el código de elementos finitos Abaqus Implicit dynamics (Abaqus, 2007). Se ha realizado un modelo 3D dinámico de la viga sándwich rotaria. El modelo consta de varios sólidos con diferentes propiedades y tamaños (Fig. 3A):

• Viga sándwich: con propiedades de sólido deformable que, a su vez, presenta dos regiones bien diferenciadas de materiales diferentes (pieles de material compuesto y núcleo de nido de abeja de Nomex®) (Fig. 4). Su longitud es de 480 mm.

• Parte rígida: con propiedades de sólido que permite simular un eje físico de rotación. Su longitud es de 30 mm.

Ambos sólidos se unen con una interacción tipo tie, nomenclatura de Abaqus, que impide el desplazamiento relativo entre ambos. De igual manera, como se puede ver en la figura 3B, las pieles y el núcleo de la viga sándwich se unen mediante una interacción tie.

La velocidad de giro se ha modelado como un campo predefinido constante de velocidad angular sobre toda la viga y se ha definido un tiempo de simulación de los modelos suficiente para estudiar siete revoluciones completas de la viga, ya que con estas se alcanza la convergencia de los resultados, y se genera un dato cada 100 ?s.

Con relación al mallado, se han utilizado tres tipos de elementos (Fig. 4). Para la parte rígida, se han usado elementos rígidos triangulares lineales de tres nodos (R3D3 según la nomenclatura de Abaqus). Para las pieles, se han utilizado elementos hexaédricos de ocho nodos, de integración reducida y control de hourglass (SC8R según la nomenclatura de Abaqus). Por último, para el modelado del núcleo de nido de abeja, se han utilizado elementos tipo membrana (Shell) triangulares lineales de tres nodos (S3 según la nomenclatura de Abaqus). La malla del modelo comprende, aproximadamente, 100.000 elementos y 160.000 nodos. Para determinar su tamaño adecuado se ha realizado un análisis de sensibilidad hasta observar una convergencia de los resultados.

 

2.3 Obtención de las frecuencias

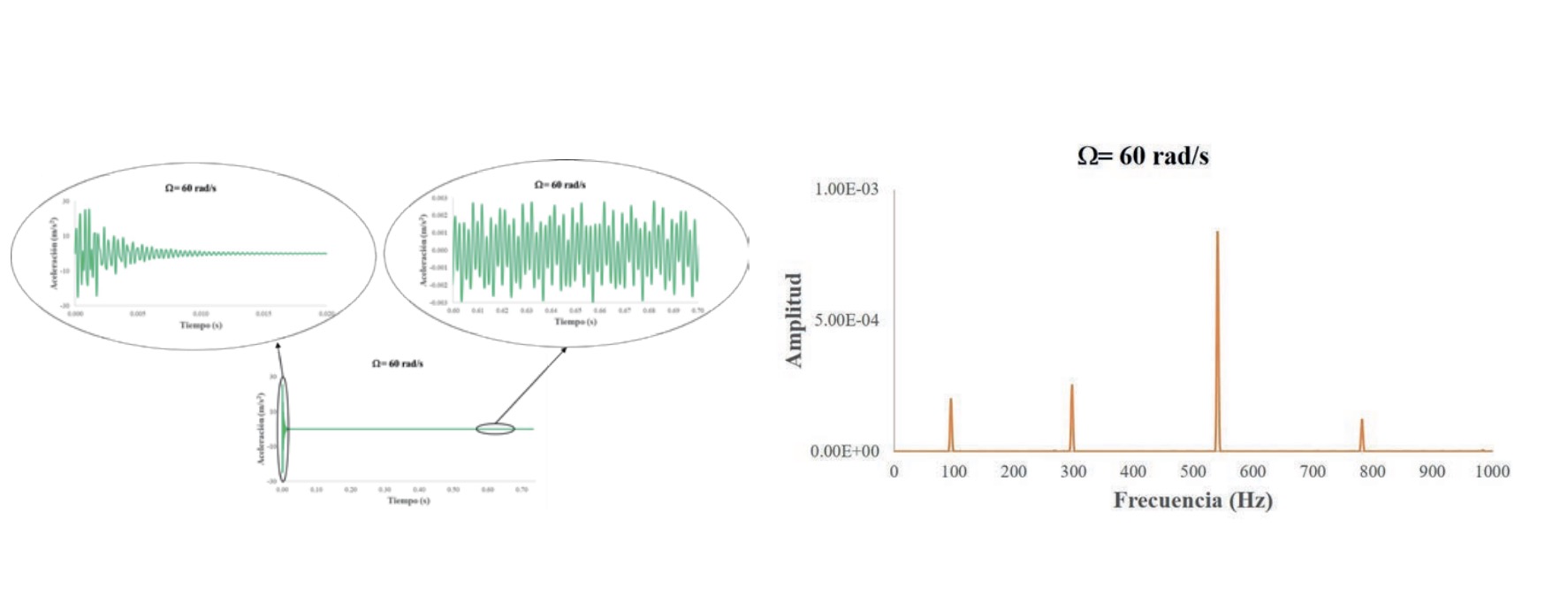
La obtención de las frecuencias naturales a partir del modelo numérico se ha realizado mediante un análisis en el dominio de la frecuencia de las aceleraciones en la dirección Y del extremo libre de la viga. La figura 5 muestra un ejemplo de la aceleración obtenida para una viga que presenta un agujero de tamaño relativo = 0,01 y que gira a ? = 60 rad/s.

En las primeras revoluciones de la viga hay una etapa transitoria de mayor amplitud en el histórico de aceleración. Obsérvese que la escala de los ejes se ha modificado para facilitar la comprensión de cada fase. El procesamiento de la señal se ha hecho mediante la transformada rápida de Fourier. Con el fin de evitar la fase transitoria se ha utilizado la ventana kaiser, que atenúa lateralmente la señal y reduce el efecto leakage (Norton, 2003). En la figura 6 se muestra la transformada rápida de Fourier de la aceleración filtrada. Se pueden ver las cuatro primeras frecuencias naturales en el plano XY: w1 = 95,215 Hz, w2= 297,852 Hzw3= 540,771 Hz y w4= 782,470 Hz.

 

3. VALIDACIÓN DEL MODELO NUMÉRICO

Antes de obtener los resultados de las frecuencias para todos los casos considerados se procedió a validar el modelo numérico desarrollado. Para ello, se compararon los resultados obtenidos con resultados de la literatura especializada.

 

3.1 Comparación con los resultados de Lee ‘et. al’ (Lee, 2017)

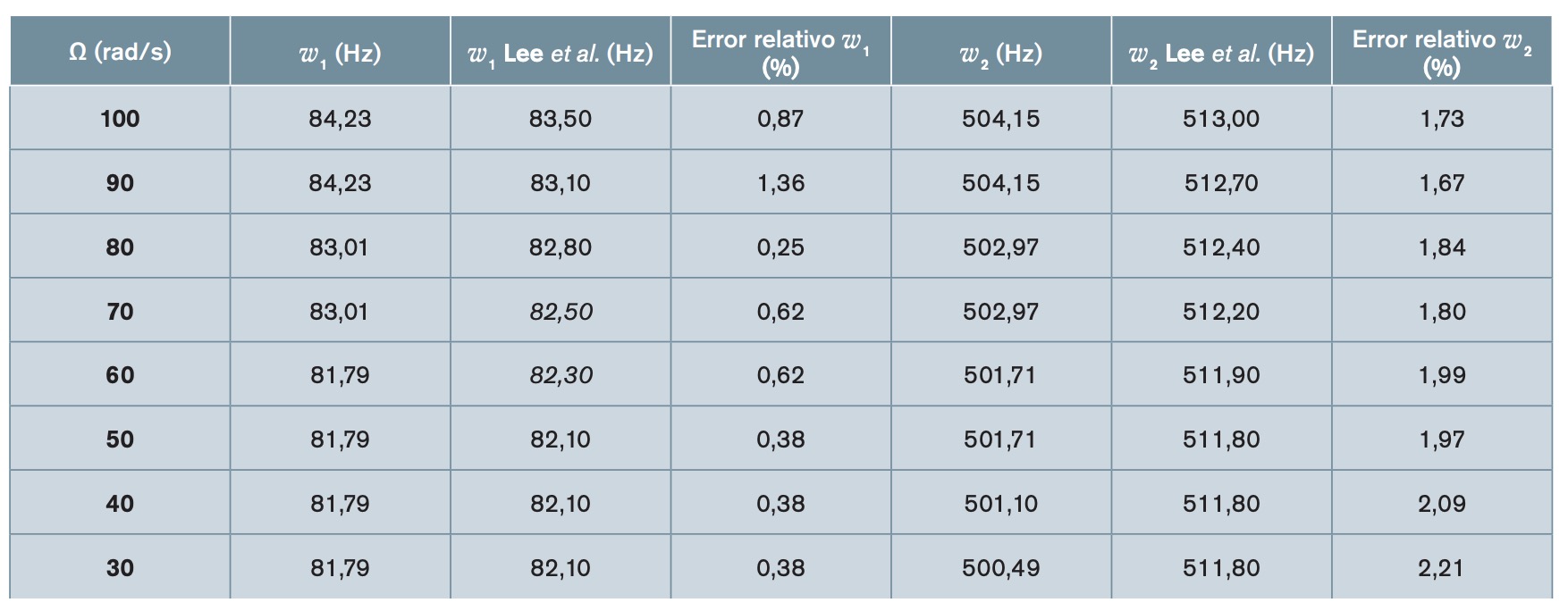
Primeramente, se han comparado los resultados con los obtenidos por Lee et al. (Lee, 2017). Puesto que en la literatura no se han encontrado resultados de las frecuencias de las vigas rotatorias de material compuesto que se han utilizado en este trabajo, con la finalidad de verificar el procedimiento se han comparado los resultados obtenidos con el modelo desarrollado fabricado con un material convencional, como es el acero, con los resultados de Lee et al. (Lee, 2017). La tabla 2 muestra la comparación de la primera y la segunda frecuencia natural para todas las velocidades de giro. También se pueden encontrar los valores de las frecuencias y los errores relativos en valor absoluto para cada velocidad. En ella se puede apreciar como los resultados de la comparación son excelentes con un error relativo máximo del 2,21%.

 

3.2 Comparación con los resultados de Pourriahi ‘et al.’ (Pourriahi, 2022)

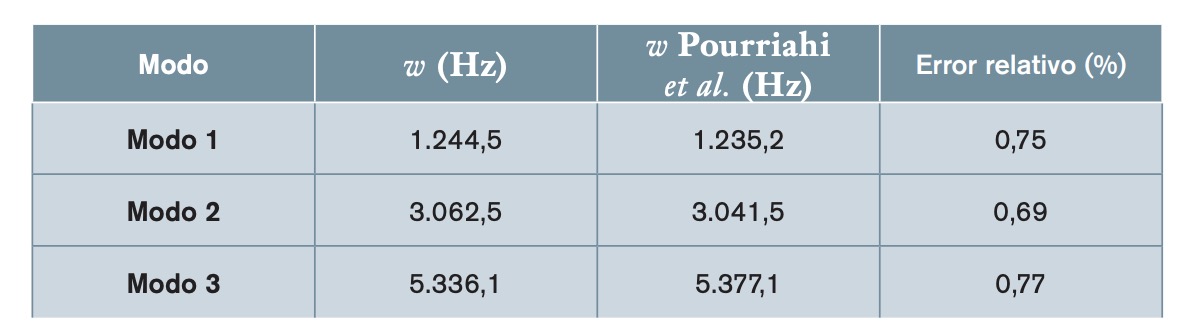
En segundo lugar, con el fin de verificar el material compuesto del modelo desarrollado, se han comparado los resultados de la viga sándwich desarrollada con los de Pourriahi et al. (Pourriahi et al., 2022). Ellos analizaron las vibraciones de una viga sándwich libre con condiciones de contorno libre-libre formada por pieles de material compuesto y núcleo de nido de abeja, al igual que la viga objeto de este trabajo. Para realizar la comparación ha sido necesario adaptar las dimensiones de la viga y el material, ya que las pieles estaban fabricadas con aluminio 7075 y el núcleo de nido de abeja estaba fabricado con aluminio 5052. En la tabla 3 se muestran los resultados de la comparación de las frecuencias naturales para tres modos distintos junto con los errores relativos. Se observa que los resultados prácticamente coinciden con unos errores relativos inferiores al 0,8%.

 

4. RESULTADOS OBTENIDOS CON EL MODELO NUMÉRICO

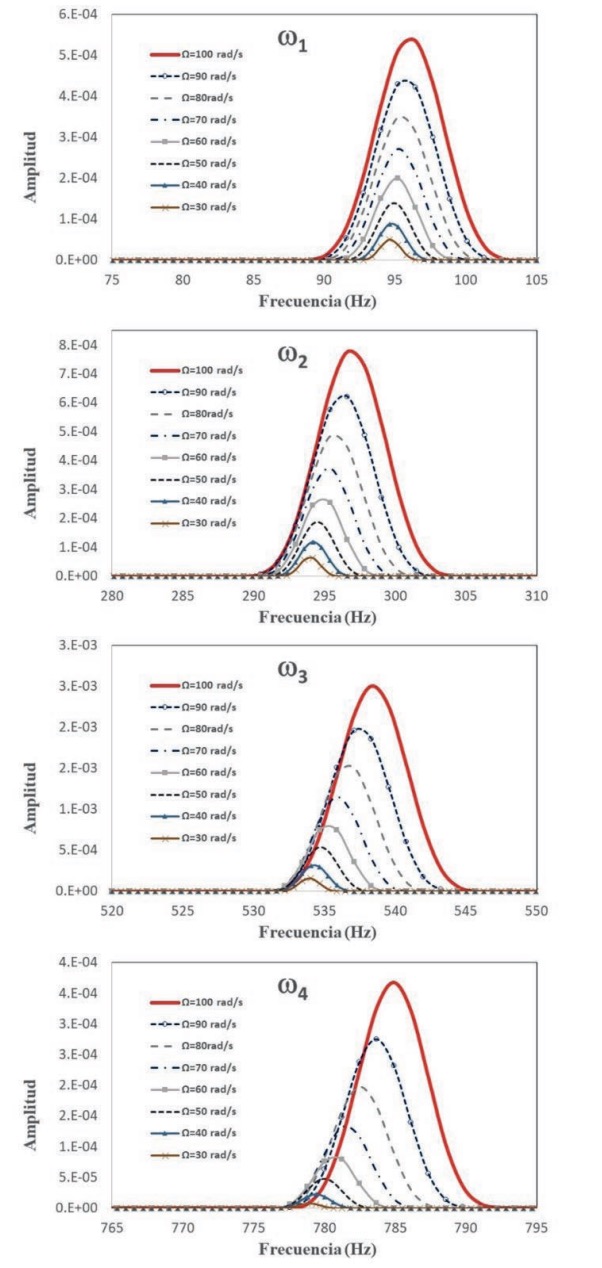
Una vez validado el modelo numérico, se obtuvieron las cuatro primeras frecuencias naturales para todos los casos considerados. En la figura 7 se muestra un ejemplo de los resultados obtenidos para la localización del defecto = 0,785 y para su tamaño = 0,02. Se ha representado la amplitud en función de la frecuencia para las cuatro primeras frecuencias naturales para las distintas velocidades de giro. Se puede observar cómo a medida que aumenta la velocidad de giro incrementa el valor de la amplitud y de frecuencia natural, lo que tiene sentido, ya que al aumentar la velocidad de giro, se incrementa la rigidez de la viga. Esta diferencia es más notable a partir de la segunda frecuencia natural. Estos resultados son análogos a los obtenidos para la viga intacta y para el resto de vigas dañadas.

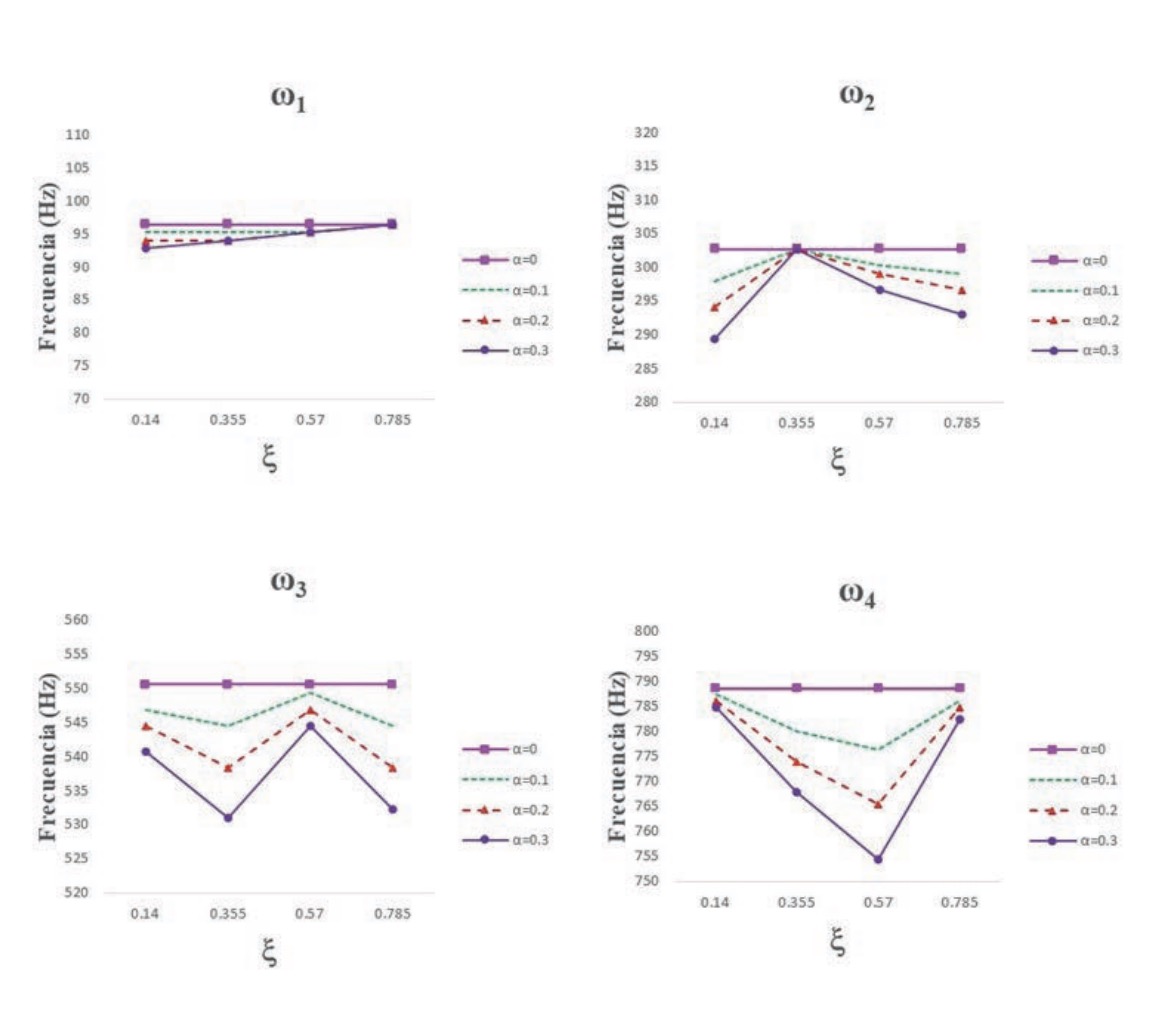
A continuación, para analizar la influencia del tamaño y la ubicación de la discontinuidad, se ha representado la frecuencia en función de la localización de la discontinuidad para sus distintos tamaños relativos. La figura 8 muestra un ejemplo de los resultados para las cuatro frecuencias naturales y para la velocidad de rotación ? = 100 rad/s. A la vista de los resultados, que son análogos a los obtenidos para las demás velocidades de rotación, puede concluirse lo siguiente:

• Para todos los casos considerados, la presencia de la discontinuidad transversal reduce el valor de las frecuencias naturales debido a un aumento de la flexibilidad local (Dimarogonas, 1996).

• En el caso de la primera frecuencia natural, se observa que el efecto del defecto es menor cuanto más alejado se encuentra del eje de giro.

• Para la segunda frecuencia natural se observa que para = 0,14 se encuentra el mínimo en el valor de la frecuencia para todos los tamaños, mientras que en alrededor de = 0,355 la frecuencia no sufre ninguna variación en función de la gravedad del defecto. Esto puede deberse a la presencia de un nodo en esa localización.

• En cuanto a la tercera frecuencia natural, se puede ver que el mínimo en el valor de la frecuencia se encuentra para todos los tamaños para las localizaciones = 0,355 y = 0,785, mientras que en = 0,57 la frecuencia apenas varía en función de la gravedad del defecto también debido a la presencia de un nodo cercano a esa localización.

• Por último, para la cuarta frecuencia natural, el mínimo en el valor de la frecuencia para todos los tamaños se encuentra en la ubicación = 0,57. En las localizaciones = 0,14 y = 0,785 la frecuencia prácticamente no varía con el tamaño de la discontinuidad.

• En resumen, observando en conjunto las gráficas de la figura 8, se puede deducir que las frecuencias naturales son posibles parámetros válidos en la detección de defectos en vigas rotatorias siempre que estén localizadas en posiciones que no estén cercanas a aquellos puntos en los que no hay variación de las frecuencias naturales en función del tamaño del defecto.

 

5. APLICACIÓN DE LA RNA

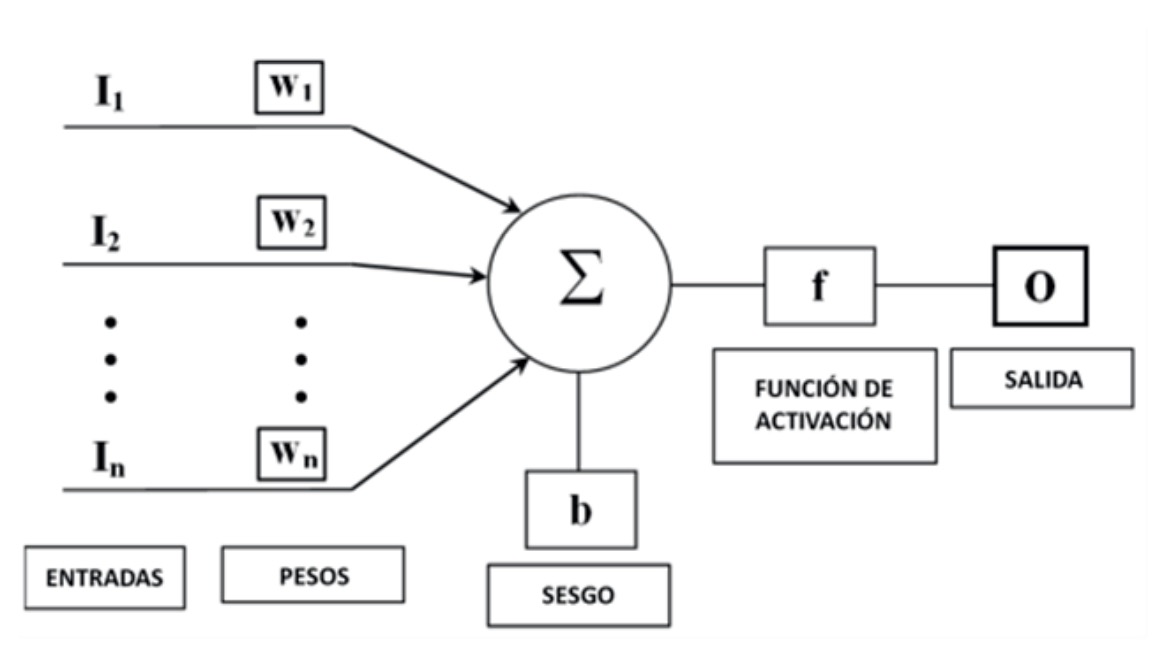
Las RNA son una herramienta matemática versátil que ha demostrado ser efectiva en la resolución de diversos problemas de ingeniería, entre otras aplicaciones. Su utilidad radica en su capacidad para identificar patrones y relaciones entre datos de entrada y salida. Estas redes buscan imitar el funcionamiento de los sistemas neuronales biológicos y están formadas por unidades denominadas neuronas. Cada neurona recibe múltiples entradas (Ii), que pueden provenir de fuentes externas o de otras neuronas dentro de la red. Luego, combina estas entradas y genera una salida. La salida (O) se determina mediante una función de activación aplicada al resultado de la suma ponderada de todas las entradas, es decir, cada entrada (Ii) se multiplica por un peso asociado (wi), y a este sumatorio se le añade un valor de sesgo (b) (Fig. 9). De esta manera, la relación matemática entre las entradas y la salida se expresa como

En este trabajo se ha empleado una red perceptrón multicapa (MLP). Este tipo de red neuronal está compuesta por una capa de entrada, una o varias capas ocultas y una capa de salida. Por lo general, cada neurona de una capa se conecta con todas las neuronas de la siguiente capa. El proceso comienza con el entrenamiento de la red, utilizando un conjunto de datos conocidos como patrones de entrenamiento. Durante esta fase, los patrones se procesan repetidamente, ajustando progresivamente los pesos de las conexiones hasta alcanzar un conjunto óptimo que genere respuestas satisfactorias. En este caso, se ha optado por el algoritmo de retropropagación para el entrenamiento, ya que es el más utilizado en redes perceptrón multicapa debido a su simplicidad y eficacia. Los datos disponibles se han dividido aleatoriamente en tres grupos, utilizados para el entrenamiento, la validación y la prueba de la red, que constan del 70%, el 15% y el 15% de los datos, respectivamente. Hay cuatro entradas (tamaño del defecto, localización del mismo, velocidad de giro y orden de frecuencia) y una salida (frecuencia natural).

Las variables utilizadas para comprobar la precisión de la red han sido el error cuadrático medio (ECM), calculado según la expresión (2) y el coeficiente de correlación R2 . Los mejores resultados se han obtenido con una red con una capa oculta, con 35 neuronas con un error cuadrático medio ECM = 2,02·10-6 y un coeficiente de correlación R2 = 0,99. (2)

6. VALIDACIÓN DE LA RED NEURONAL ARTIFICIAL PROPUESTA

La verificación de la RNA propuesta se ha realizado comparando, en primer lugar, los resultados obtenidos con los datos numéricos de referencia y, en segundo lugar, con datos que no se han utilizado en su entrenamiento.

 

6.1 Comparación con los datos numéricos de referencia

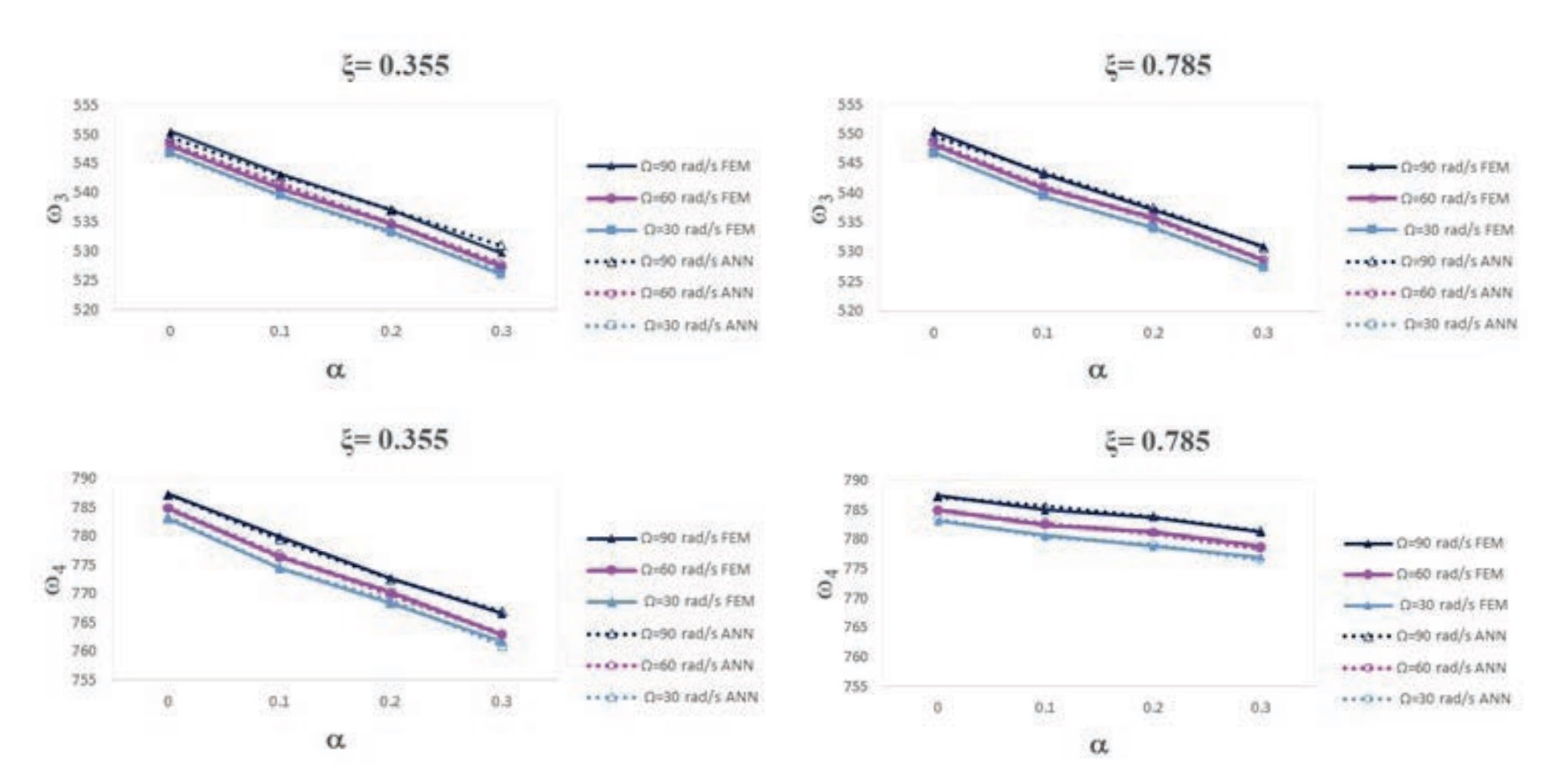
En la figura 10 se muestran los ejemplos de la comparación entre los resultados de la red propuesta y los datos numéricos de referencia para la tercera y la cuarta frecuencia natural y para las localizaciones de la discontinuidad = 0,355 y 0,785. Se han representado los valores de la frecuencia en función del tamaño del defecto para las tres velocidades de rotación ? = 30, 60 y 90 rad/s. Se puede observar que la concordancia entre los resultados obtenidos por la red y los numéricos es muy buena. Los resultados de la comparación correspondientes a otras localizaciones y a otras velocidades de giro son muy similares. Además, se ha calculado el error relativo medio (ERM) entre los resultados obtenidos con la red y los datos de referencia, de acuerdo con la ecuación (3). Teniendo en cuenta todos los casos considerados, el error obtenido es del 2%. (3)

6.2 Comparación con valores no usados en el entrenamiento de la red

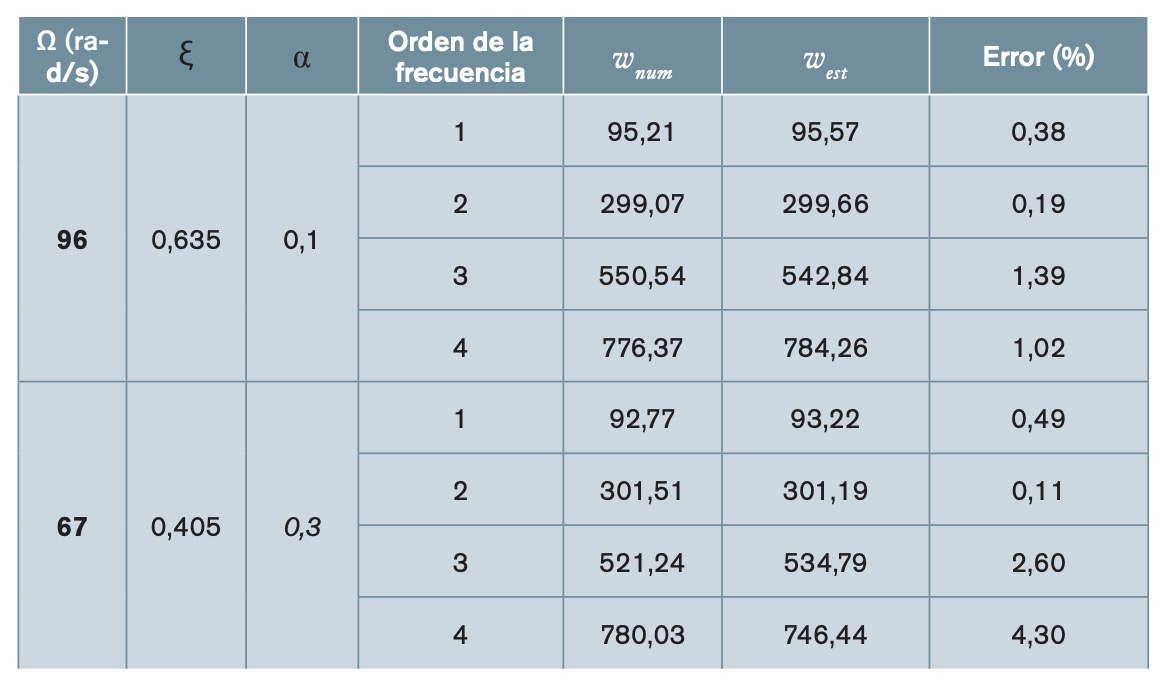
Para comprobar la robustez y precisión de la RNA propuesta se han comparado los resultados obtenidos con ella con valores no utilizados en el entrenamiento. Para ello, se han seleccionado aleatoriamente dos casos de vigas con características diferentes de las utilizadas para su entrenamiento y se han calculado las cuatro frecuencias para cada caso. En la tabla 4 se muestran los resultados obtenidos. Como puede observarse, el error es pequeño, en ninguno de los casos el error es superior al 4,5 \%.

 

7. CONCLUSIONES

En este trabajo se presenta una RNA que permite estimar los valores de las cuatro primeras frecuencias naturales de vigas de material compuesto con pieles de polímeros reforzados con fibra de carbono y núcleo de nido de abeja dañada en función de la velocidad de rotación, el tamaño y la localización del defecto. Los datos de entrada para realizar el entrenamiento de la RNA se han conseguido a partir de un modelo numérico dinámico 3D de una viga sándwich con una discontinuidad transversal en el núcleo. La metodología propuesta ofrece muy buenos resultados. Si los valores estimados por la red se comparan con los datos utilizados para la formulación de la red, el error relativo medio es del 2%. Si la comparación se realiza con valores obtenidos del modelo numérico, diferentes de los utilizados en la elaboración de la red, la estimación, como era de esperar, es ligeramente peor, pero en ningún caso supera el 4,5%. Por tanto, la RNA propuesta representa una alternativa muy efectiva para analizar la respuesta vibratoria de vigas sándwich dañadas, y destaca por su eficiencia, facilidad de uso y bajo costo computacional.

 

BIBLIOGRAFÍA

Abaqus (2007). Abaqus theory manual, version 6.7, in: Dassault Systemes Inc.

Bhat RB (1986). Transverse vibrations of a rotating uniform cantilever beam with tip mass as predicted by using beam characteristic orthogonal polynomials in the Rayleigh-Ritz Method. Journal of Sound and Vibration 105(2):199-210. Chen LW,

Chen CL (1988). Vibration and stability of crack thick rotating blades. Computers Structures 28: 67-74.

Dimarogonas AD (1996). Vibration of cracked structures: A state of the art review”. Engineering Fracture Mechanics 55 (5): 831-57.

Honeycomb Core & Flex-Core Material & Manufacturers. Disponible en: https://www.toraytac.com/ products/adhesives-and-core/honeycomb-core (consultado el 17 de julio de 2023).

Kim SS, Kim JH (2003). Rotating composite beam with a breathing crack. Composite Structures 60:83-90.

Lee JW, Lee JY (2017). In-plane bending vibration analysis of a rotating beam with multiple edge cracks by using the transfer matrix method. Meccanica 52:1143-57.

Marsh G (2005). Wind turbines. How big can they get? Refocus 6 (2):22- 8.

Norton MP, Karczub DG (2003). Fundamentals of noise and vibration analysis for engineers. Second edition, Cambridge University Press, Cambridge (UK).

Ozdemir O, Kaya MO (2014). Energy Derivation and Extension-Flapwise Bending Vibration Analysis of a Rotating Piezo-laminated Composite Timoshenko Beam. Mechanics of Advanced Materials and Structures 21:477-89.

Pourriahi V, Heidari-Rarani M, Isfahani AT (2022). Influence of geometric parameters on free vibration behavior of an aluminium honeycomb core sandwich beam using experimentally validated finite element models. Journal of Sandwich Structures & Materials 24 (2):1449-69.

Ridgard C (2008). Complex Structures for Manned/ Unmanned Aerial Vehicles. Delivery Order 0019: Low Temp Composite Processing Mechanical Property Data. Air Force Research Laboratory.

Sekhar A (2008). Multiple cracks effects and identification. Mechanical Systems and Signal Processing 22: 845-78.

Sezgin EF (2008). Mechanical Behaviour and Modeling of Honeycomb Cored Laminated Fiber/ Polymer Sandwich Structures. Thesis (Master), Izmir Institute of Technology.

Valverde-Marcos B, Muñoz Abella B, Rubio L, Rubio P (2022). Influence of the rotation speed on the dynamic behaviour of a cracked rotating beam. Theoretical and applied fracture mechanics 117:103209.

Youngho K, Junyoung J, Wanjo R, Dong-Whan C (2012). Multiple defect diagnostics of gas turbine engine using SVM and RCGA-based ann algorithms. Journal of Mechanical Science and Technology 26(5):1623-32.